Z-score สามารถเป็นลบได้หรือไม่?
ในสถิติ คะแนน z บอกเราว่าค่าหนึ่งๆ มาจาก ค่าเฉลี่ย เป็นจำนวนเท่าใด เราใช้สูตรต่อไปนี้เพื่อคำนวณคะแนน z:
z = (X – μ) / σ
โดยที่ X คือค่าที่เรากำลังวิเคราะห์ μ คือค่าเฉลี่ย และ σ คือค่าเบี่ยงเบนมาตรฐาน
คะแนน z อาจเป็นค่าบวก ลบ หรือศูนย์ก็ได้
คะแนน z เชิงบวกบ่งชี้ว่าค่าใดค่าหนึ่งสูงกว่าค่าเฉลี่ย คะแนน z ที่เป็นลบบ่งชี้ว่าค่าใดค่าหนึ่งนั้นต่ำกว่าค่าเฉลี่ย และคะแนน az ที่เป็นศูนย์บ่งชี้ว่าค่าใดค่าหนึ่งเท่ากับค่าเฉลี่ย
ตัวอย่างบางส่วนควรทำให้สิ่งนี้ชัดเจน
ตัวอย่าง: การคำนวณคะแนน Z
สมมติว่าเรามีชุดข้อมูลต่อไปนี้ที่แสดงความสูง (เป็นนิ้ว) ของพืชบางกลุ่ม:
5, 7, 7, 8, 9, 10, 13, 17, 17, 18, 19, 19, 20
ค่าเฉลี่ยตัวอย่างของชุดข้อมูลนี้คือ 13 และค่าเบี่ยงเบนมาตรฐานตัวอย่างคือ 5.51
1. ค้นหาคะแนน z ของค่า “8” ในชุดข้อมูลนี้
วิธีคำนวณคะแนน z มีดังนี้
z = (X – μ) / σ = (8 – 13) / 5.51 = -0.91
ซึ่งหมายความว่าค่า “8” คือ 0.91 ส่วนเบี่ยงเบนมาตรฐาน ที่ต่ำกว่า ค่าเฉลี่ย
2. ค้นหาคะแนน z ของค่า “13” ในชุดข้อมูลนี้
วิธีคำนวณคะแนน z มีดังนี้
z = (X – μ) / σ = (13 – 13) / 5.46 = 0
ซึ่งหมายความว่าค่า “13” เท่ากับค่าเฉลี่ยทุกประการ
3. ค้นหาคะแนน z ของค่า “20” ในชุดข้อมูลนี้
วิธีคำนวณคะแนน z มีดังนี้
z = (X – μ) / σ = (20 – 13) / 5.46 = 1.28
ซึ่งหมายความว่าค่า “20” คือ 1.28 ส่วนเบี่ยงเบนมาตรฐาน ที่อยู่เหนือ ค่าเฉลี่ย
วิธีการตีความคะแนน Z
แผนภูมิ AZ บอกเราว่าเปอร์เซ็นต์ของค่าที่อยู่ต่ำกว่าคะแนน Z ที่กำหนด ตัวอย่างบางส่วนควรทำให้สิ่งนี้ชัดเจน
ตัวอย่างที่ 1: คะแนน Z ติดลบ
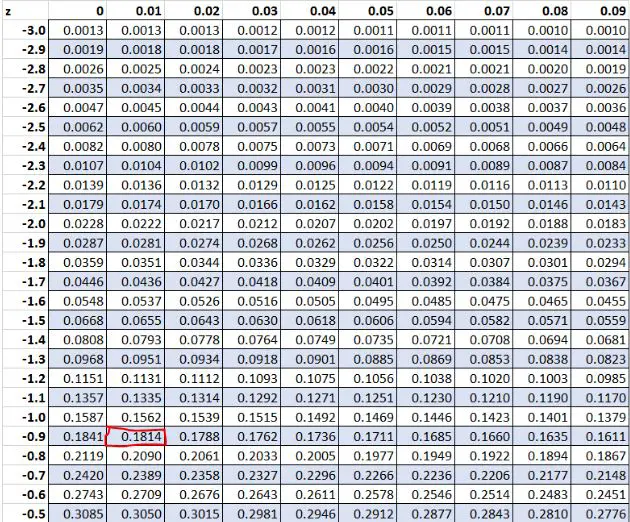
ก่อนหน้านี้ เราพบว่าค่าดิบ “8” ในชุดข้อมูลของเรามีคะแนน z -0.91 ตามตาราง Z พบว่า 18.14% ของค่าต่ำกว่าค่านี้
ตัวอย่างที่ 2: คะแนน Z เท่ากับศูนย์
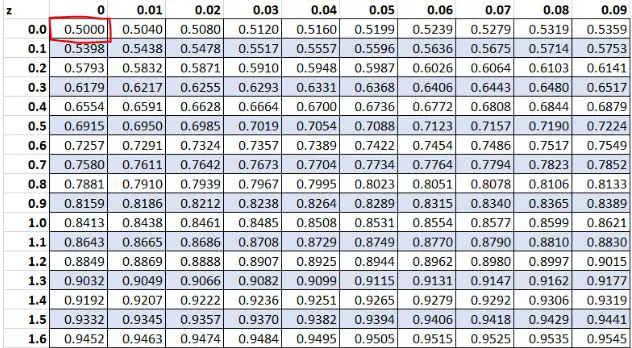
ก่อนหน้านี้ เราพบว่าค่าดิบ “13” ในชุดข้อมูลของเรามีคะแนน z เป็น 0 ตามตาราง Z พบว่า 50.00% ของค่าน้อยกว่าค่านี้
ตัวอย่างที่ 3: คะแนน Z บวก
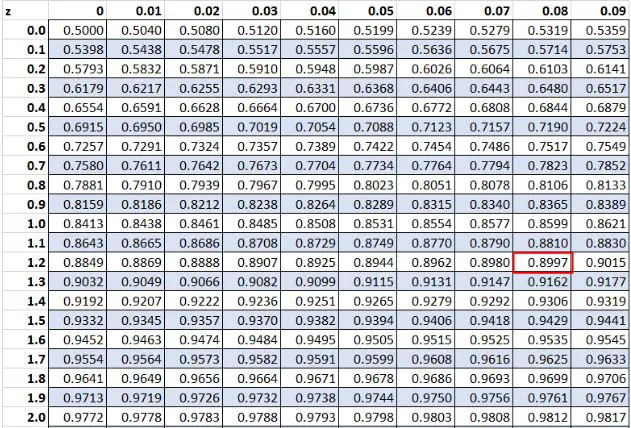
ก่อนหน้านี้ เราพบว่าค่าดิบ “20” ในชุดข้อมูลของเรามีคะแนน z เท่ากับ 1.28 ตามตาราง Z พบว่า 89.97% ของค่าต่ำกว่าค่านี้
บทสรุป
คะแนน Z สามารถใช้ค่าใดก็ได้ระหว่างค่าอนันต์ลบและค่าอนันต์บวก แต่คะแนน z ส่วนใหญ่อยู่ภายใน 2 ส่วนเบี่ยงเบนมาตรฐานของค่าเฉลี่ย จริงๆ แล้วมีกฎในสถิติที่เรียกว่า กฎทั่วไป ซึ่งระบุว่าสำหรับชุดข้อมูลที่กำหนดด้วยการแจกแจงแบบปกติ:
- 68% ของค่าข้อมูลอยู่ภายในค่าเบี่ยงเบนมาตรฐานหนึ่งของค่าเฉลี่ย
- 95% ของค่าข้อมูลอยู่ภายในค่าเบี่ยงเบนมาตรฐานสองค่าของค่าเฉลี่ย
- 99.7% ของค่าข้อมูลอยู่ภายในค่าเบี่ยงเบนมาตรฐานสามค่าของค่าเฉลี่ย
ยิ่งค่าสัมบูรณ์ของคะแนน z สูงเท่าใด ค่าดิบก็จะยิ่งมาจากค่าเฉลี่ยของชุดข้อมูลมากขึ้นเท่านั้น ยิ่งค่าสัมบูรณ์ของคะแนน z ยิ่งต่ำ ค่าดิบก็จะยิ่งใกล้กับค่าเฉลี่ยของชุดข้อมูลมากขึ้นเท่านั้น
หัวข้อที่เกี่ยวข้อง: