ค่า f ที่สูงหมายถึงอะไรใน anova
การวิเคราะห์ความแปรปรวนแบบทางเดียว ใช้เพื่อพิจารณาว่าค่าเฉลี่ยของกลุ่มอิสระตั้งแต่ 3 กลุ่มขึ้นไปเท่ากันหรือไม่
การวิเคราะห์ความแปรปรวนทางเดียวใช้สมมติฐานว่างและทางเลือกต่อไปนี้:
- H 0 : ค่าเฉลี่ยกลุ่มทั้งหมดเท่ากัน
- HA : ค่าเฉลี่ยกลุ่มอย่างน้อยหนึ่งกลุ่มแตกต่างจากค่าเฉลี่ยอื่นๆ
ทุกครั้งที่คุณทำการวิเคราะห์ความแปรปรวนแบบทางเดียว คุณจะพบกับตารางสรุปที่มีลักษณะดังนี้:
| แหล่งที่มา | ผลรวมของกำลังสอง (SS) | df | ค่าเฉลี่ยกำลังสอง (MS) | เอฟ | ค่า P |
|---|---|---|---|---|---|
| การรักษา | 192.2 | 2 | 96.1 | 2,358 | 0.1138 |
| ข้อผิดพลาด | 1100.6 | 27 | 40.8 | ||
| ทั้งหมด | 1292.8 | 29 |
ค่า F ในตารางคำนวณได้ดังนี้:
- ค่า F = การประมวลผลกำลังสองเฉลี่ย / ข้อผิดพลาดกำลังสองเฉลี่ย
อีกวิธีในการเขียนสิ่งนี้คือ:
- ค่า F = ความแปรผันระหว่างค่าเฉลี่ยตัวอย่าง / ความแปรผันภายในตัวอย่าง
หากความแปรผันระหว่างค่าเฉลี่ยตัวอย่างสูงเมื่อเทียบกับความแปรผันภายในแต่ละตัวอย่าง ค่า F จะมีค่ามาก
ตัวอย่างเช่น ค่า F ในตารางด้านบนมีการคำนวณดังนี้
- ค่า F = 96.1 / 40.8 = 2.358
ในการค้นหา ค่า p ที่สอดคล้องกับค่า F นี้ เราสามารถใช้ เครื่องคำนวณการกระจายตัวแบบ F โดยมีองศาอิสระในตัวเศษ = df การรักษา และองศาอิสระในตัวส่วน = ข้อผิดพลาด df
ตัวอย่างเช่น ค่า p ที่สอดคล้องกับค่า F เท่ากับ 2.358 ตัวเศษ df = 2 และตัวส่วน df = 27 คือ 0.1138
เนื่องจากค่า p นี้ไม่น้อยกว่า α = 0.05 เราจึงไม่สามารถปฏิเสธสมมติฐานว่างได้ ซึ่งหมายความว่าไม่มีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างค่าเฉลี่ยของทั้งสามกลุ่ม
ดูค่า F ของ ANOVA
เพื่อให้เข้าใจถึงค่า F ในตาราง ANOVA ได้โดยสัญชาตญาณ ให้พิจารณาตัวอย่างต่อไปนี้
สมมติว่าเราต้องการทำการวิเคราะห์ความแปรปรวนแบบทางเดียวเพื่อตรวจสอบว่าเทคนิคการศึกษาที่แตกต่างกันสามเทคนิคทำให้เกิดคะแนนสอบเฉลี่ยที่แตกต่างกันหรือไม่ ตารางต่อไปนี้แสดงผลการสอบของนักเรียน 10 คนที่ใช้แต่ละเทคนิค:
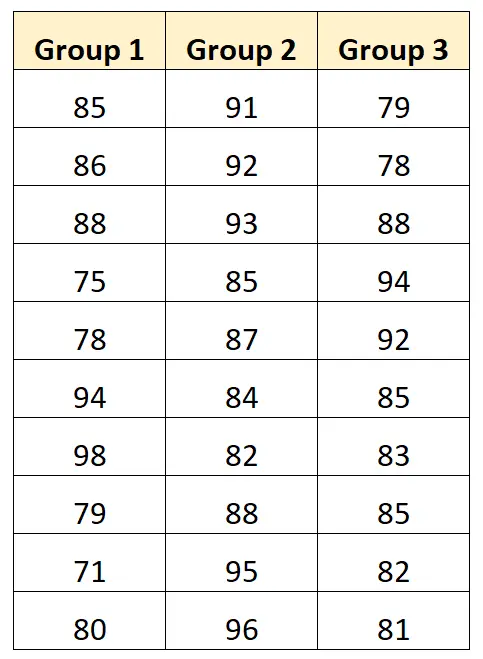
เราสามารถสร้างแผนภูมิต่อไปนี้เพื่อแสดงภาพผลการสอบแยกตามกลุ่ม:
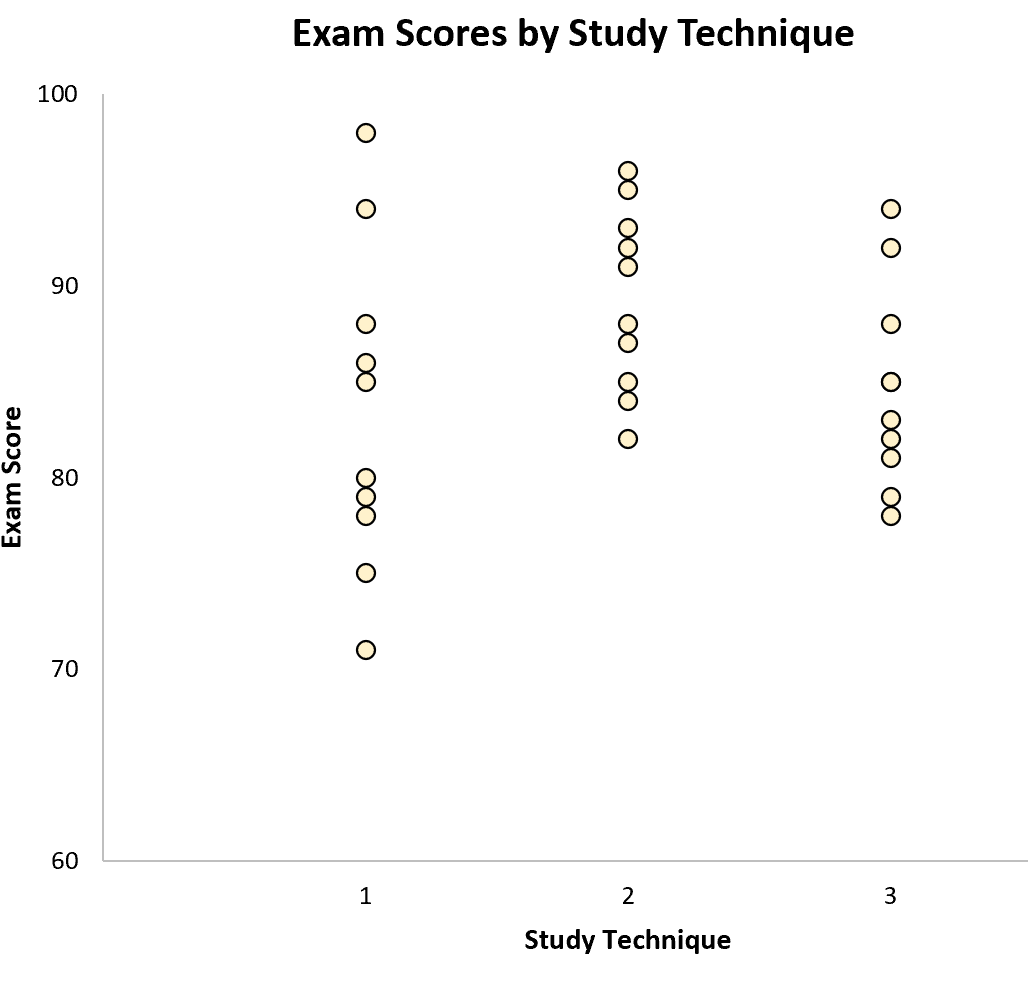
ความแปรผัน ภายใน ตัวอย่างแสดงโดยการแจกแจงค่าภายในแต่ละตัวอย่าง:
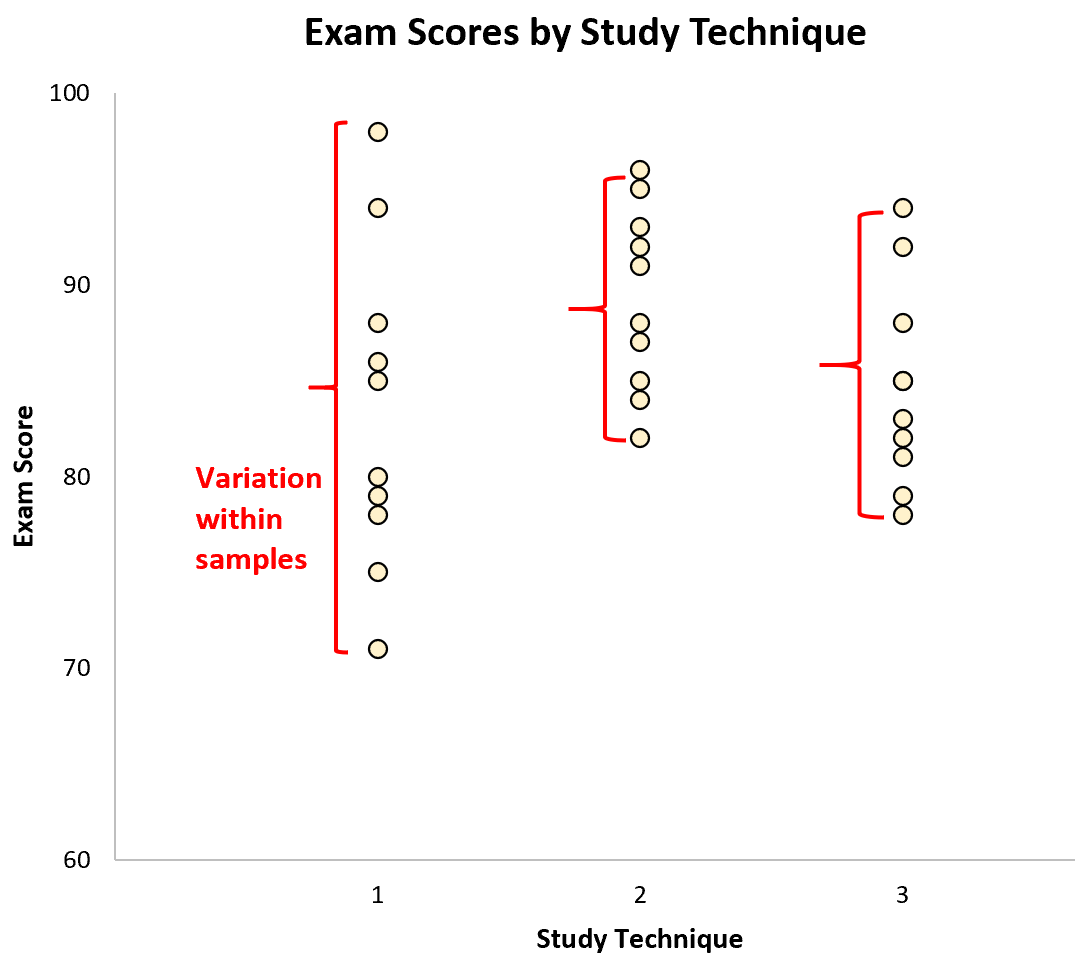
ความแปรผัน ระหว่าง ตัวอย่างแสดงด้วยความแตกต่างระหว่างค่าเฉลี่ยตัวอย่าง:
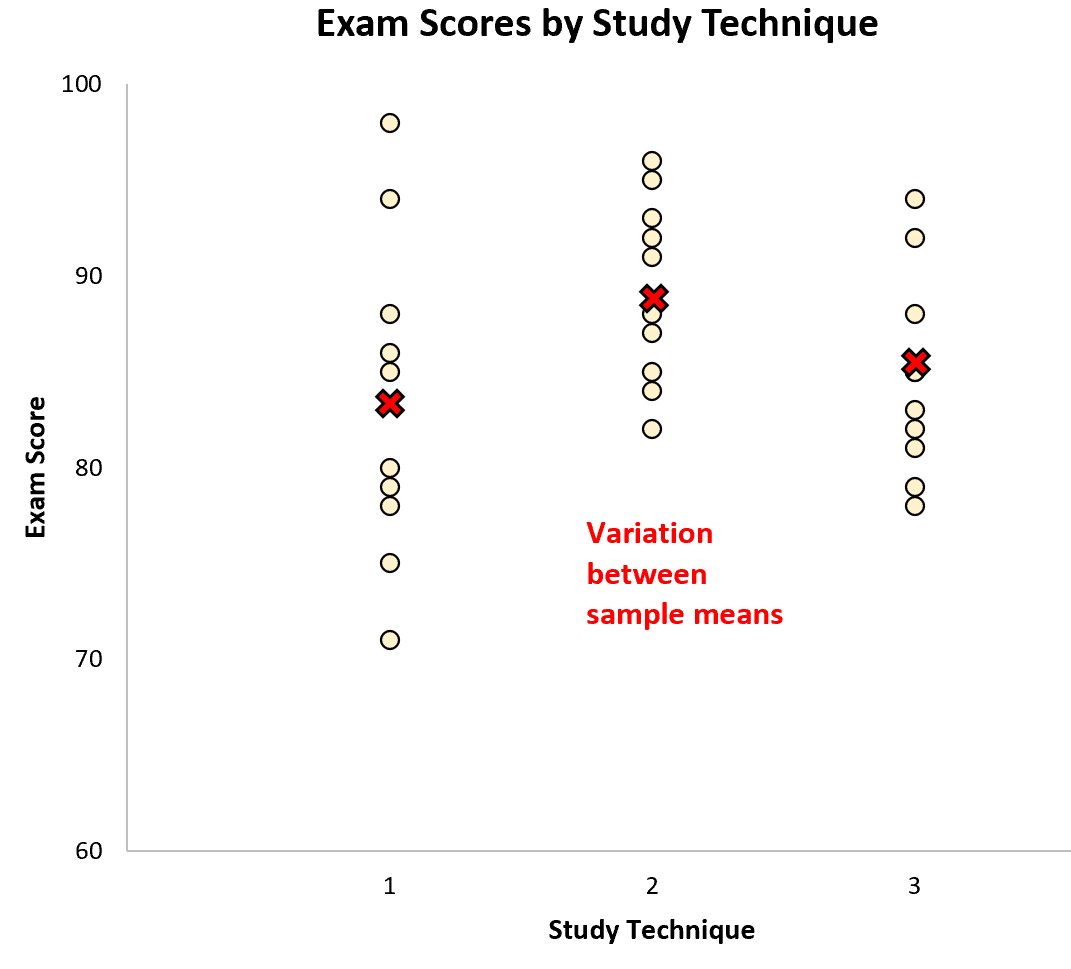
เมื่อใช้การวิเคราะห์ความแปรปรวนทางเดียวสำหรับชุดข้อมูลนี้ เราพบว่าค่า F เท่ากับ 2.358 และค่า p ที่สอดคล้องกันคือ 0.1138
เนื่องจากค่า p นี้ไม่น้อยกว่า 0.05 เราจึงไม่สามารถปฏิเสธสมมติฐานว่างได้ ซึ่งหมายความว่าเราไม่มีหลักฐานเพียงพอที่จะบอกว่าเทคนิคการศึกษาที่ใช้ส่งผลให้เกิดความแตกต่างที่มีนัยสำคัญทางสถิติในคะแนนสอบโดยเฉลี่ย
กล่าวอีกนัยหนึ่ง สิ่งนี้บอกเราว่าความแปรผันระหว่างค่าเฉลี่ยตัวอย่างไม่สูงพอที่จะสัมพันธ์กับความแปรผันภายในตัวอย่างที่จะปฏิเสธสมมติฐานว่าง
บทสรุป
นี่เป็นบทสรุปโดยย่อของประเด็นหลักของบทความนี้:
- ค่า F ใน ANOVA คำนวณเป็น: ความแปรผันระหว่างค่าเฉลี่ยตัวอย่าง / ความแปรผันภายในตัวอย่าง
- ยิ่งค่า F ใน ANOVA สูง ความแปรผันระหว่างค่าเฉลี่ยตัวอย่างก็จะยิ่งมากขึ้นเมื่อเทียบกับความแปรผันภายในตัวอย่าง
- ยิ่งค่า F สูง ค่า p ที่สอดคล้องกันก็จะยิ่งต่ำลง
- หากค่า p ต่ำกว่าเกณฑ์ที่กำหนด (เช่น α = 0.05) เราสามารถปฏิเสธสมมติฐานว่างของ ANOVA และสรุปได้ว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างค่าเฉลี่ยกลุ่ม
แหล่งข้อมูลเพิ่มเติม
วิธีการดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวใน Excel
วิธีดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวด้วยตนเอง
เครื่องคิดเลข ANOVA แบบทางเดียว