วิธีทำการทดสอบ dunnett ใน r

การทดสอบภายหลังเฉพาะกิจ คือการทดสอบประเภทหนึ่งที่ดำเนินการตาม ANOVA เพื่อพิจารณาว่าค่าเฉลี่ยของกลุ่มใดมีความแตกต่างกันอย่างมีนัยสำคัญทางสถิติ

หากกลุ่มการศึกษากลุ่มใดกลุ่มหนึ่งถือเป็น กลุ่มควบคุม เราก็ควรใช้ การทดสอบ Dunnett เป็นการทดสอบหลังการทดสอบ

บทช่วยสอนนี้จะอธิบายวิธีดำเนินการทดสอบ Dunnett ใน R

ตัวอย่าง: การทดสอบ Dunnett ใน R

สมมติว่าครูต้องการทราบว่าเทคนิคการเรียนรู้ใหม่สองเทคนิคมีศักยภาพในการปรับปรุงคะแนนสอบของนักเรียนหรือไม่ เพื่อทดสอบสิ่งนี้ เธอสุ่มแบ่งชั้นเรียนที่มีนักเรียน 30 คนออกเป็นสามกลุ่มดังต่อไปนี้:

• กลุ่มควบคุม: นักเรียน 10 คน
• นักเรียนศึกษาด้านเทคนิคใหม่ 1:10
• การศึกษาด้านเทคนิคใหม่ 2: 10 นักเรียน

หลังจากใช้เทคนิคการเรียนที่ได้รับมอบหมายมาหนึ่งสัปดาห์ นักเรียนแต่ละคนจะสอบแบบเดียวกัน

เราสามารถใช้ขั้นตอนต่อไปนี้ใน R เพื่อสร้างชุดข้อมูล แสดงภาพค่าเฉลี่ยของกลุ่ม ดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียว และสุดท้ายทำการทดสอบของ Dunnett เพื่อพิจารณาว่าเทคนิคการศึกษาใหม่ใด (ถ้ามี) ที่ให้ผลลัพธ์ที่แตกต่างกันเมื่อเปรียบเทียบกับกลุ่มควบคุม .

ขั้นตอนที่ 1: สร้างชุดข้อมูล

รหัสต่อไปนี้แสดงวิธีสร้างชุดข้อมูลที่มีผลการสอบของนักเรียนทั้ง 30 คน:

 #create data frame
data <- data.frame(technique = rep (c("control", "new1", "new2"), each = 10 ),
                   score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89,
                             81, 82, 83, 83, 83, 84, 87, 90, 92, 93,
                             77, 78, 79, 88, 89, 90, 91, 95, 95, 98))

#view first six rows of data frame
head(data)

  technical score
1 control 76
2 controls 77
3 controls 77
4 controls 81
5 controls 82
6 controls 82

ขั้นตอนที่ 2: ดูผลการสอบของแต่ละกลุ่ม

รหัสต่อไปนี้แสดงวิธีสร้าง boxplots เพื่อให้เห็นภาพการกระจายผลการสอบสำหรับแต่ละกลุ่ม:

 boxplot(score ~ technique,
        data = data,
        main = "Exam Scores by Studying Technique",
        xlab = "Studying Technique",
        ylab = "Exam Scores",
        col = "steelblue",
        border = "black")

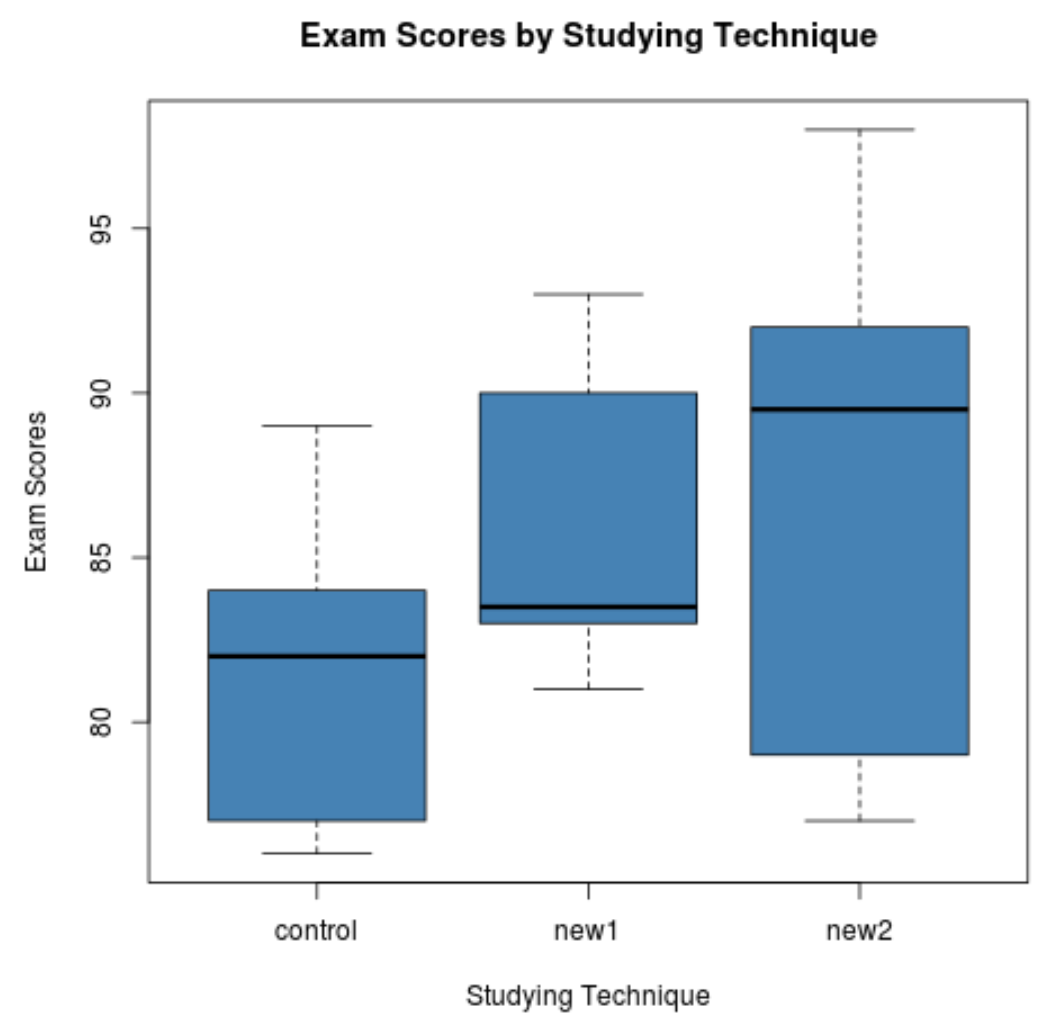
จากแผนภาพกล่อง เราจะเห็นว่าการกระจายคะแนนสอบในแต่ละเทคนิคการเรียนแตกต่างกันมาก จากนั้นเราจะทำการวิเคราะห์ความแปรปรวนแบบทางเดียวเพื่อพิจารณาว่าความแตกต่างเหล่านี้มีนัยสำคัญทางสถิติหรือไม่

ที่เกี่ยวข้อง: วิธีการพล็อตหลายกล่องในแผนภูมิเดียวใน R

ขั้นตอนที่ 3: ดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียว

รหัสต่อไปนี้แสดงวิธีดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวเพื่อทดสอบความแตกต่างระหว่างคะแนนสอบเฉลี่ยในแต่ละกลุ่ม:

 #fit the one-way ANOVA model
model <- aov(score ~ technique, data = data)

#view model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)  
technical 2 211.5 105.73 3.415 0.0476 *
Residuals 27 836.0 30.96                 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

เนื่องจากค่า p-value โดยรวม ( 0.0476 ) น้อยกว่า 0.05 แสดงว่าแต่ละกลุ่มมีคะแนนสอบเฉลี่ยไม่เท่ากัน ต่อไป เราจะทำการทดสอบ Dunnett เพื่อพิจารณาว่าเทคนิคการศึกษาใดที่ให้คะแนนสอบเฉลี่ยที่แตกต่างจากกลุ่มควบคุม

ขั้นตอนที่ 4: ทำการทดสอบ Dunnett

ในการทำการทดสอบ Dunnett ใน R เราสามารถใช้ฟังก์ชัน DunnettTest() จากไลบรารี DescTools ซึ่งใช้ไวยากรณ์ต่อไปนี้:

การทดสอบดันเน็ตต์(x, g)

ทอง:

• x: เวกเตอร์ตัวเลขของค่าข้อมูล (เช่น ผลการสอบ)
• g: เวกเตอร์ที่ระบุชื่อกลุ่ม (เช่น เทคนิคการศึกษา)

รหัสต่อไปนี้แสดงวิธีใช้ฟังก์ชันนี้สำหรับตัวอย่างของเรา:

 #load DescTools library
library(DescTools)

#perform Dunnett's Test
DunnettTest(x=data$score, g=data$technique)

  Dunnett's test for comparing several treatments with a control:  
    95% family-wise confidence level

$control
             diff lwr.ci upr.ci pval    
new1-control 4.2 -1.6071876 10.00719 0.1787    
new2-control 6.4 0.5928124 12.20719 0.0296 *  

---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1' '1.' 0.1 ' ' 1

วิธีการตีความผลลัพธ์มีดังนี้:

• ความแตกต่างโดยเฉลี่ยของคะแนนสอบระหว่างเทคนิคการศึกษาใหม่ 1 และกลุ่มควบคุมคือ 4.2 ค่า p ที่สอดคล้องกันคือ 0.1787
• ความแตกต่างโดยเฉลี่ยของคะแนนสอบระหว่างเทคนิคการศึกษาใหม่ 2 และกลุ่มควบคุมคือ 6.4 ค่า p ที่สอดคล้องกันคือ 0.0296

จากผลการวิจัยพบว่าการเรียนเทคนิคที่ 2 เป็นเทคนิคเดียวที่สร้างคะแนนสอบเฉลี่ยที่แตกต่างจากกลุ่มควบคุมอย่างมีนัยสำคัญ (p = 0.0296)

แหล่งข้อมูลเพิ่มเติม

ข้อมูลเบื้องต้นเกี่ยวกับการวิเคราะห์ความแปรปรวนแบบทางเดียว
วิธีดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวใน R
วิธีทำการทดสอบ Tukey ใน R