ตัวอย่างการทดสอบทีแบบจับคู่: คำจำกัดความ สูตร และตัวอย่าง

การทดสอบทีแบบจับคู่ตัวอย่าง ใช้เพื่อเปรียบเทียบค่าเฉลี่ยของสองตัวอย่าง เมื่อ การสังเกต แต่ละครั้งในตัวอย่างหนึ่งสามารถเชื่อมโยงกับการสังเกตในอีกตัวอย่างหนึ่งได้

บทช่วยสอนนี้จะอธิบายสิ่งต่อไปนี้:

• แรงจูงใจในการดำเนินการจับคู่ตัวอย่าง t-test
• สูตรสำหรับดำเนินการทดสอบตัวอย่างแบบจับคู่
• สมมติฐานที่ต้องปฏิบัติตามเพื่อทำการทดสอบค่าทีแบบคู่
• ตัวอย่างวิธีการจับคู่ตัวอย่าง t-test

ตัวอย่างคู่ทดสอบที: แรงจูงใจ

โดยทั่วไปการทดสอบทีแบบคู่จะใช้ในสองสถานการณ์:

1. มีการวัดผลก่อนและหลังการรักษา เช่น วัดการกระโดดในแนวดิ่งสูงสุดของผู้เล่นบาสเกตบอลระดับวิทยาลัยก่อนและหลังเข้าร่วมโปรแกรมการฝึกอบรม

2. การวัดจะดำเนินการภายใต้เงื่อนไขสองประการที่แตกต่างกัน ตัวอย่างเช่น เวลาตอบสนองของผู้ป่วยจะถูกวัดด้วยยาสองตัวที่แตกต่างกัน

ในทั้งสองกรณี เราต้องการเปรียบเทียบการวัดเฉลี่ยระหว่างสองกลุ่ม โดยที่การสังเกตแต่ละครั้งจากตัวอย่างหนึ่งสามารถเชื่อมโยงกับการสังเกตจากตัวอย่างอื่นได้

ตัวอย่างที่จับคู่ทดสอบที: สูตร

ตัวอย่างทีทดสอบที่จับคู่กันจะใช้สมมติฐานว่างต่อไปนี้เสมอ:

• H ₀ : μ ₁ = μ ₂ (ค่าเฉลี่ยประชากรทั้งสองเท่ากัน)

สมมติฐานทางเลือกอาจเป็นแบบทวิภาคี ซ้าย หรือขวา:

• H ₁ (สองด้าน): μ ₁ ≠ μ ₂ (ค่าเฉลี่ยของประชากรทั้งสองไม่เท่ากัน)
• H ₁ (ซ้าย): μ ₁ < μ ₂ (ค่าเฉลี่ยของประชากร 1 ต่ำกว่าค่าเฉลี่ยของประชากร 2)
• H ₁ (ขวา): μ ₁ > μ ₂ (ค่าเฉลี่ยของประชากร 1 มากกว่าค่าเฉลี่ยของประชากร 2)

เราใช้สูตรต่อไปนี้เพื่อคำนวณสถิติการทดสอบที:

t = x _{ส่วนต่าง} / (s _{ส่วนต่าง} /√n)

ทอง:

• x _diff : ตัวอย่างค่าเฉลี่ยของความแตกต่าง
• s: ตัวอย่างค่าเบี่ยงเบนมาตรฐานของผลต่าง
• n: ขนาดตัวอย่าง (เช่น จำนวนคู่)

หากค่า p ที่สอดคล้องกับสถิติการทดสอบทีด้วยระดับความเป็นอิสระ (n-1) น้อยกว่าระดับนัยสำคัญที่เลือก (ตัวเลือกทั่วไปคือ 0.10, 0.05 และ 0.01) คุณสามารถปฏิเสธสมมติฐานว่างได้

ตัวอย่างคู่ทดสอบที: สมมติฐาน

เพื่อให้ผลลัพธ์ของการทดสอบค่าทีที่จับคู่กันถูกต้อง ต้องเป็นไปตามสมมติฐานต่อไปนี้:

• ผู้เข้าร่วมควรได้รับการสุ่มเลือกจากประชากร
• ความแตกต่างระหว่างคู่ควรกระจายตามปกติโดยประมาณ
• ไม่ควรมีค่าผิดปกติที่รุนแรงในความแตกต่าง

ตัวอย่าง การจับ คู่ t-test : ตัวอย่าง

สมมติว่าเราต้องการทราบว่าโปรแกรมการฝึกบางอย่างสามารถเพิ่มการกระโดดในแนวดิ่งสูงสุด (หน่วยเป็นนิ้ว) ของผู้เล่นบาสเกตบอลระดับวิทยาลัยได้หรือไม่

เพื่อทดสอบสิ่งนี้ เราสามารถ สุ่มตัวอย่างง่ายๆ จากผู้เล่นบาสเก็ตบอลระดับวิทยาลัย 20 คน และวัดการกระโดดในแนวดิ่งสูงสุดแต่ละครั้ง จากนั้นเราจะให้ผู้เล่นแต่ละคนใช้โปรแกรมการฝึกเป็นเวลาหนึ่งเดือน แล้ววัดการกระโดดแนวดิ่งสูงสุดของพวกเขาอีกครั้งในช่วงปลายเดือน

เพื่อตรวจสอบว่าโปรแกรมการฝึกส่งผลต่อการกระโดดในแนวตั้งสูงสุดจริงหรือไม่ เราจะทำการทดสอบทีแบบคู่ที่ระดับนัยสำคัญ α = 0.05 โดยใช้ขั้นตอนต่อไปนี้:

ขั้นตอนที่ 1: คำนวณข้อมูลสรุปสำหรับความแตกต่าง

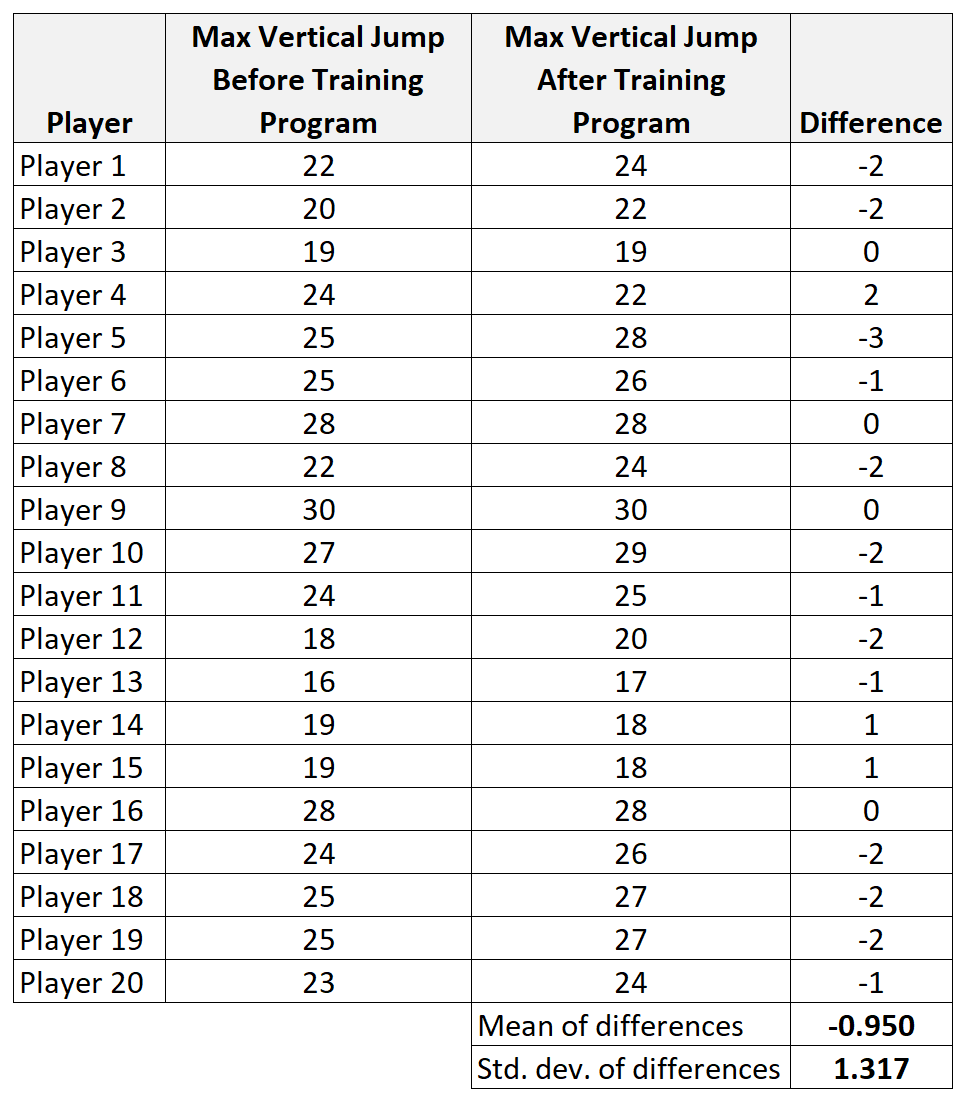
• x _diff : ค่าเฉลี่ยตัวอย่างความแตกต่าง = -0.95
• s: ตัวอย่างค่าเบี่ยงเบนมาตรฐานของผลต่าง = 1.317
• n: ขนาดตัวอย่าง (เช่น จำนวนคู่) = 20

ขั้นตอนที่ 2: กำหนดสมมติฐาน

เราจะทำการทดสอบทีสำหรับตัวอย่างที่จับคู่กับสมมติฐานต่อไปนี้:

• H ₀ : μ ₁ = μ ₂ (ค่าเฉลี่ยประชากรทั้งสองเท่ากัน)
• H ₁ : μ ₁ ≠ μ ₂ (ค่าเฉลี่ยประชากรทั้งสองไม่เท่ากัน)

ขั้นตอนที่ 3: คำนวณสถิติ t -test

t = x _{ส่วนต่าง} / (ส่วน _ต่าง /√n) = -0.95 / (1.317/ √ 20) = -3.226

ขั้นตอนที่ 4: คำนวณค่า p-value ของสถิติการทดสอบ t-

ตาม คะแนน T ของเครื่องคิดเลขค่า P ค่า p ที่เกี่ยวข้องกับ t = -3.226 และองศาอิสระ = n-1 = 20-1 = 19 คือ 0.00445

ขั้นตอนที่ 5: วาดข้อสรุป

เนื่องจากค่า p นี้ต่ำกว่าระดับนัยสำคัญของเรา α = 0.05 เราจึงปฏิเสธสมมติฐานว่าง เรามีหลักฐานเพียงพอที่จะบอกว่าการกระโดดแนวตั้งสูงสุดโดยเฉลี่ยของผู้เล่นแตกต่างกันทั้งก่อนและหลังเข้าร่วมโปรแกรมการฝึกซ้อม

หมายเหตุ: คุณยังสามารถทำการทดสอบทีแบบคู่ตัวอย่างทั้งหมดนี้ได้โดยใช้ เครื่องคำนวณการทดสอบทีแบบจับคู่ตัวอย่าง

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้จะอธิบายวิธีดำเนินการตัวอย่างทีทดสอบแบบจับคู่โดยใช้โปรแกรมทางสถิติต่างๆ:

วิธีดำเนินการทดสอบตัวอย่างแบบจับคู่ใน Excel
วิธีดำเนินการทดสอบตัวอย่างแบบจับคู่ใน SPSS
วิธีดำเนินการทดสอบตัวอย่างแบบจับคู่ใน Stata
วิธีดำเนินการจับคู่ตัวอย่าง t-Test บนเครื่องคิดเลข TI-84
วิธีดำเนินการทดสอบตัวอย่างแบบจับคู่ใน R
วิธีดำเนินการทดสอบตัวอย่างแบบจับคู่ใน Python
วิธีทำการทดสอบ T-Test แบบจับคู่ด้วยมือ