วิธีดำเนินการทดสอบตัวอย่างแบบจับคู่ใน excel

การทดสอบทีแบบจับคู่ตัวอย่าง ใช้เพื่อเปรียบเทียบค่าเฉลี่ยของสองตัวอย่าง เมื่อการสังเกตแต่ละครั้งในตัวอย่างหนึ่งสามารถเชื่อมโยงกับการสังเกตในอีกตัวอย่างหนึ่งได้

บทช่วยสอนนี้จะอธิบายวิธีการดำเนินการตัวอย่างทีทดสอบใน Excel

วิธีดำเนินการทดสอบตัวอย่างแบบจับคู่ใน Excel

สมมติว่าเราต้องการทราบว่าหลักสูตรหนึ่งๆ มีผลกระทบอย่างมีนัยสำคัญต่อผลการเรียนของนักเรียนในการสอบนั้นๆ หรือไม่ เพื่อทดสอบสิ่งนี้ เราขอให้นักเรียน 20 คนในชั้นเรียนทำแบบทดสอบล่วงหน้า จากนั้นให้นักเรียนแต่ละคนมีส่วนร่วมในหลักสูตรเป็นเวลาสองสัปดาห์ จากนั้นให้นักเรียนทำแบบทดสอบความยากที่คล้ายกันอีกครั้ง

เพื่อเปรียบเทียบความแตกต่างระหว่างคะแนนเฉลี่ยของการทดสอบครั้งแรกและครั้งที่สอง เราใช้ตัวอย่าง t-test ที่จับคู่กัน เนื่องจากสำหรับนักเรียนแต่ละคน คะแนนในการทดสอบครั้งแรกสามารถเชื่อมโยงกับคะแนนในการทดสอบครั้งที่สองได้

รูปภาพต่อไปนี้แสดงคะแนนสอบก่อนและหลังสอบของนักเรียนแต่ละคน:

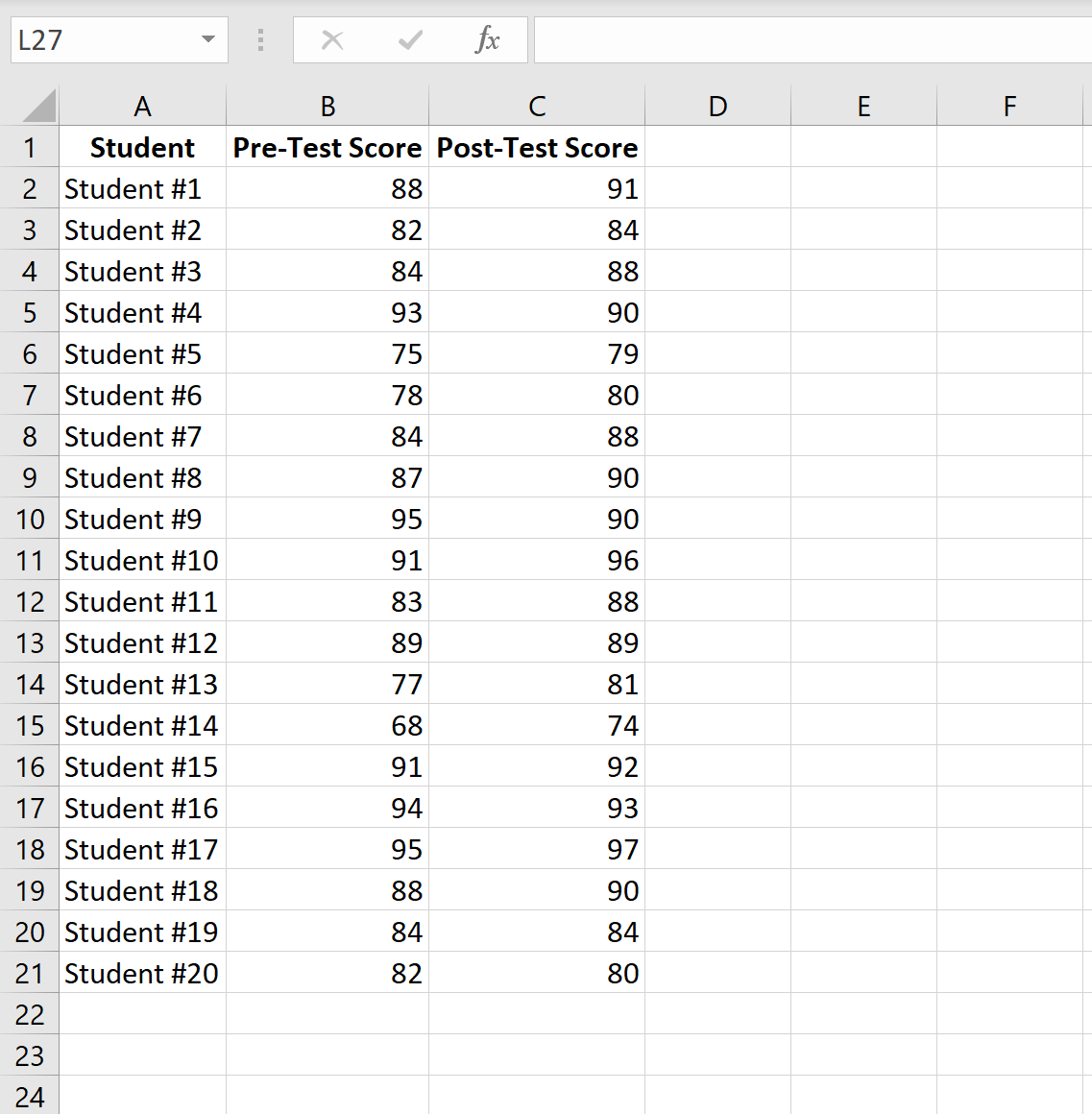
ทำตามขั้นตอนต่อไปนี้ให้เสร็จสิ้นเพื่อทำการทดสอบทีแบบจับคู่เพื่อตรวจสอบว่าคะแนนการทดสอบเฉลี่ยระหว่างการทดสอบก่อนและหลังการทดสอบมีความแตกต่างอย่างมีนัยสำคัญหรือไม่

ขั้นตอนที่ 1: เปิด Data Analysis ToolPak

ในแท็บข้อมูลของ Ribbon ด้านบน คลิก “การวิเคราะห์ข้อมูล”

หากคุณไม่เห็นตัวเลือกนี้ให้คลิก คุณต้อง ดาวน์โหลด Analysis ToolPak ซึ่งไม่มีค่าใช้จ่ายใดๆ ทั้งสิ้น

ขั้นตอนที่ 2: เลือกการทดสอบที่เหมาะสมที่จะใช้

เลือกตัวเลือกที่ระบุว่า T-Test: Matched Two Sample for Means จากนั้นคลิก OK

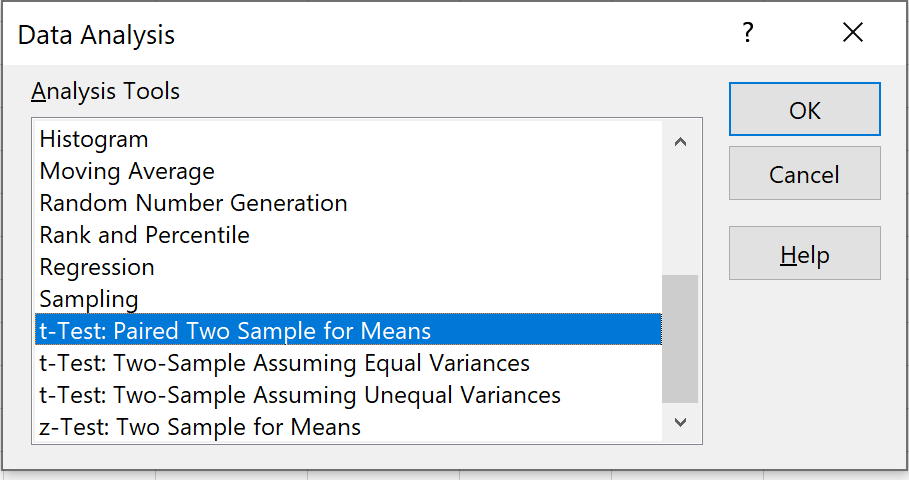
ขั้นตอนที่ 3: ป้อนข้อมูลที่จำเป็น

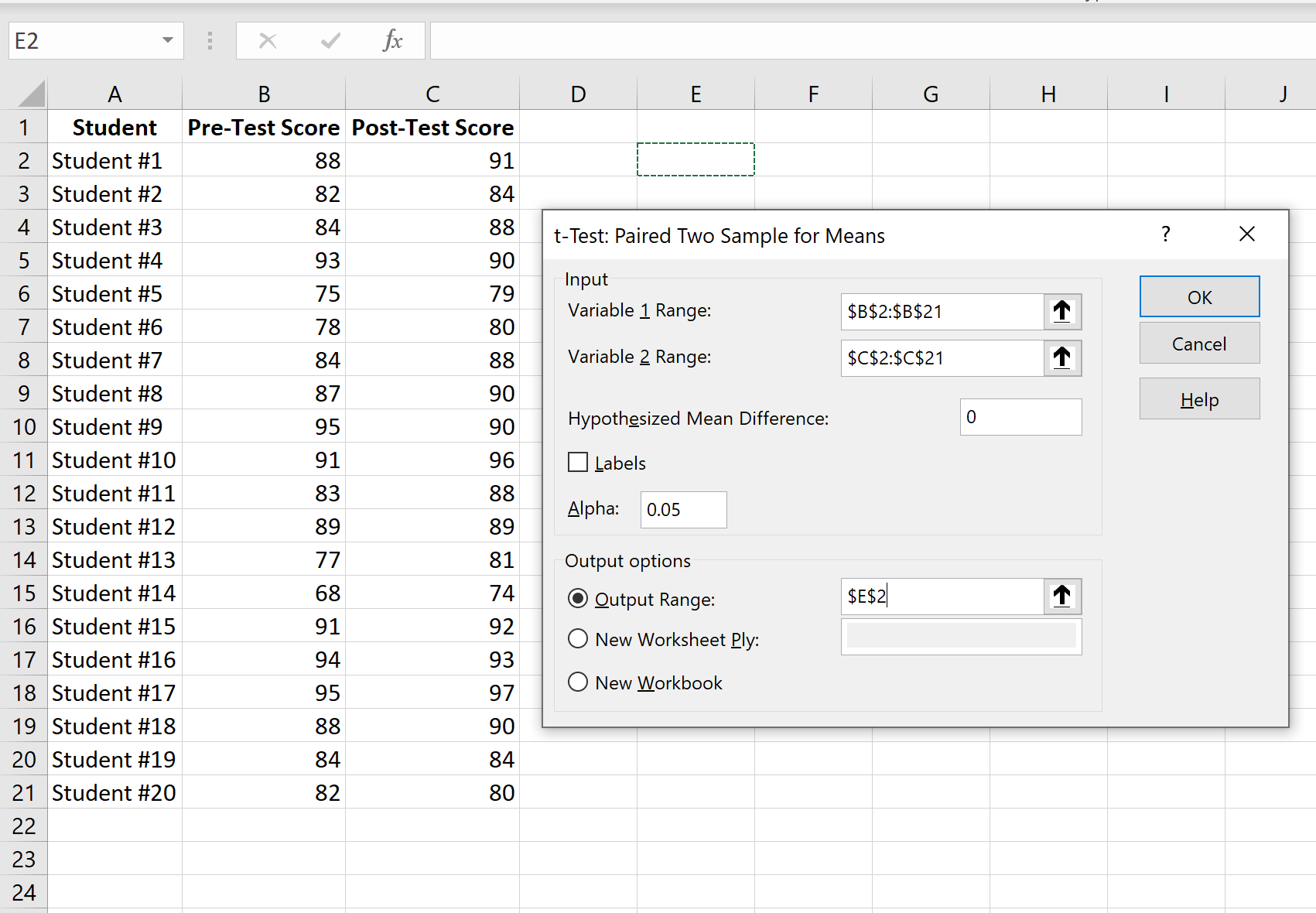
ใส่ช่วงค่าของตัวแปร 1 (คะแนนก่อนสอบ), ตัวแปร 2 (คะแนนหลังสอบ), ผลต่างค่าเฉลี่ยสมมุติ (ในกรณีนี้เราใส่ “0” เพราะเราต้องการทราบว่าความแตกต่างจริงหรือไม่ ค่าเฉลี่ยระหว่างคะแนนก่อนสอบและหลังสอบคือ 0) และช่วงผลลัพธ์ที่เราต้องการเห็นผลการทดสอบที่แสดง จากนั้นคลิกตกลง

ขั้นตอนที่ 4: ตีความผลลัพธ์

เมื่อคุณคลิกตกลงในขั้นตอนก่อนหน้า ผลการทดสอบทีจะแสดงขึ้น

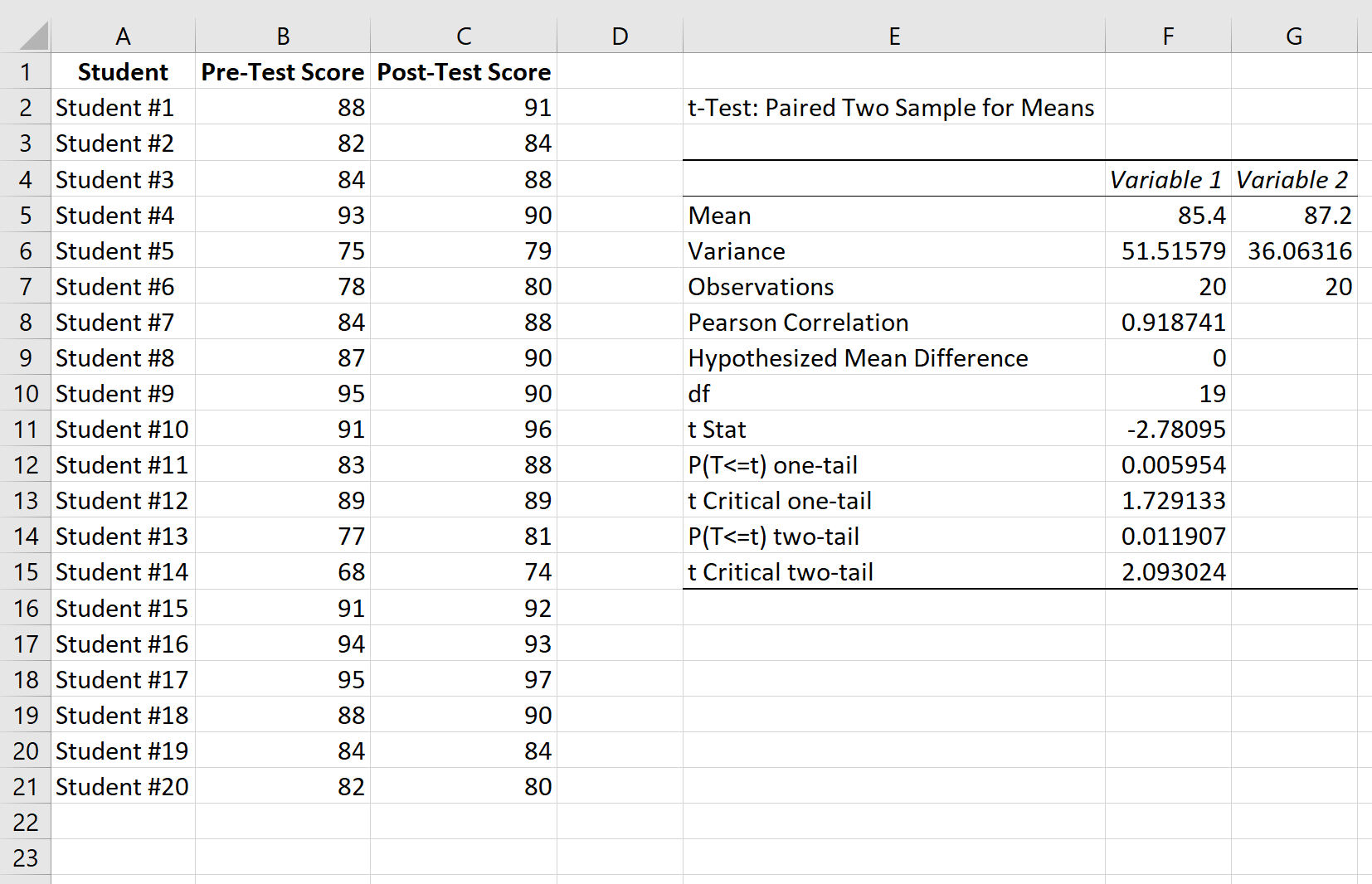
ต่อไปนี้เป็นวิธีการตีความผลลัพธ์:

ค่าเฉลี่ย: นี่คือค่าเฉลี่ยของแต่ละตัวอย่าง คะแนนสอบก่อนสอบเฉลี่ย 85.4 และคะแนนสอบหลังสอบเฉลี่ย 87.2

ความแปรปรวน: นี่คือความแปรปรวนสำหรับแต่ละตัวอย่าง ความแปรปรวนของคะแนนก่อนสอบคือ 51.51 และความแปรปรวนของคะแนนหลังสอบคือ 36.06

การสังเกต: นี่คือจำนวนการสังเกตในแต่ละตัวอย่าง ตัวอย่างทั้งสองมีการสังเกต 20 รายการ

Pearson Correlation: ความสัมพันธ์ระหว่างคะแนนก่อนสอบและคะแนนหลังสอบ กลายเป็น 0.918 .

ความแตกต่างเฉลี่ยสมมุติ: จำนวนที่เรา “ตั้งสมมติฐาน” คือความแตกต่างระหว่างสองค่าเฉลี่ย ในกรณีนี้ เราเลือก 0 เพราะต้องการทดสอบว่าคะแนนก่อนสอบและหลังสอบมีความแตกต่างกันหรือไม่

df: องศาอิสระสำหรับการทดสอบ t ซึ่งคำนวณเป็น n-1 โดยที่ n คือจำนวนคู่ ในกรณีนี้ df = 20 – 1 = 19

t Stat: สถิติการทดสอบ t ซึ่งกลายเป็น -2.78

P แบบสองด้าน(T<=t): ค่า p สำหรับการทดสอบแบบสองด้าน ในกรณีนี้ p = 0.011907 . ซึ่งน้อยกว่าอัลฟ่า = 0.05 ดังนั้นเราจึงปฏิเสธสมมติฐานว่าง เรามีหลักฐานเพียงพอที่จะบอกว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างคะแนนเฉลี่ยก่อนสอบและหลังสอบ

ค่าวิกฤตแบบสองด้าน: นี่คือค่าวิกฤตของการทดสอบ ซึ่งพบได้จากการระบุค่าในตาราง การแจกแจงแบบ t ที่สอดคล้องกับการทดสอบแบบสองด้านโดยมีค่า alpha = 0.05 และ df = 19 ซึ่งกลายเป็น 2 093024 . เนื่องจากค่าสัมบูรณ์ของสถิติการทดสอบ t ของเรามากกว่าค่านี้ เราจึงปฏิเสธสมมติฐานว่าง เรามีหลักฐานเพียงพอที่จะบอกว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างคะแนนเฉลี่ยก่อนสอบและหลังสอบ

โปรดทราบว่าทั้งวิธีค่า p และค่าวิกฤตจะนำไปสู่ข้อสรุปเดียวกัน

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้จะอธิบายวิธีดำเนินการทดสอบทีอื่นๆ ใน Excel:

วิธีดำเนินการทดสอบทีตัวอย่างเดียวใน Excel
วิธีดำเนินการทดสอบทีสองตัวอย่างใน Excel