วิธีการตีความอัตราส่วนอัตราต่อรอง

ในสถิติ ความน่า จะเป็นหมายถึงโอกาสที่เหตุการณ์จะเกิดขึ้น มีการคำนวณดังนี้:

ความน่าจะเป็น:

P(เหตุการณ์) = (# ผลลัพธ์ที่ต้องการ) / (# ผลลัพธ์ที่เป็นไปได้)

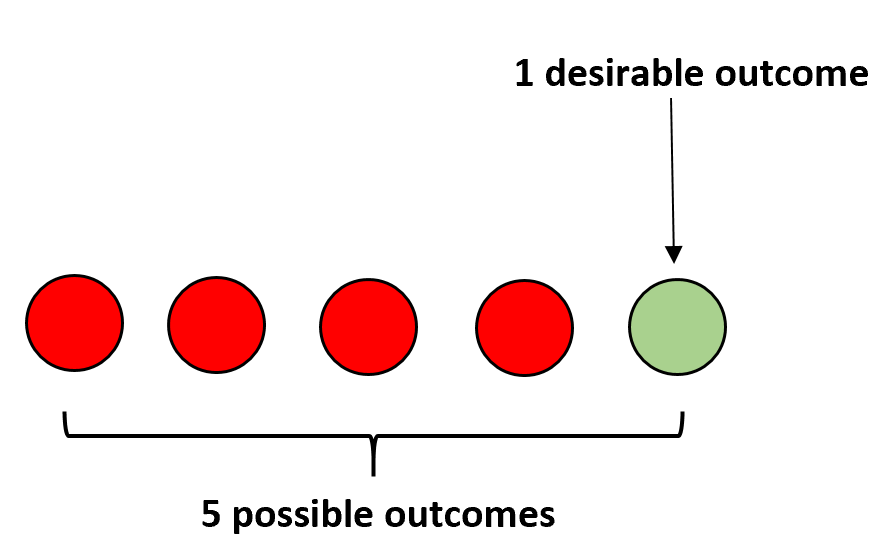
ตัวอย่างเช่น สมมติว่าเรามีลูกบอลสีแดงสี่ลูกและลูกบอลสีเขียวหนึ่งลูกในถุง หากคุณหลับตาแล้วเลือกลูกบอลแบบสุ่ม ความน่าจะเป็นที่คุณเลือกลูกบอลสีเขียวจะถูกคำนวณดังนี้:

P(สีเขียว) = 1/5 = 0.2 .

โอกาส ของเหตุการณ์ที่เกิดขึ้นสามารถคำนวณได้ดังนี้:

อัตราต่อรอง:

โอกาส (เหตุการณ์) = P (เหตุการณ์เกิดขึ้น) / 1-P (เหตุการณ์เกิดขึ้น)

เช่น อัตราต่อรองการยิงลูกบอลสีเขียวคือ (0.2)/1-(0.2) = 0.2/0.8 = 0.25

อัตราต่อรอง คืออัตราส่วนของความน่าจะเป็นสองประการ

รายงานโชค:

อัตราต่อรอง = อัตราต่อรองของเหตุการณ์ A / อัตราต่อรองของเหตุการณ์ B

ตัวอย่างเช่น เราสามารถคำนวณอัตราส่วนอัตราต่อรองระหว่างการเลือกลูกบอลสีแดงและลูกบอลสีเขียว

ความน่าจะเป็นที่จะได้ลูกบอลสีแดงคือ 4/5 = 0.8

โอกาสในการจับลูกบอลสีแดงคือ (0.8) / 1-(0.8) = 0.8 / 0.2 = 4

อัตราต่อรอง ในการเลือกลูกบอลสีแดงมากกว่าลูกบอลสีเขียวคำนวณดังนี้:

ราคาต่อรอง (สีแดง) / ราคาต่อรอง (สีเขียว) = 4 / 0.25 = 16

ดังนั้นโอกาสในการยิงลูกบอลสีแดงจึงมากกว่าโอกาสในการยิงลูกบอลสีเขียวถึง 16 เท่า

อัตราส่วนอัตราต่อรองถูกใช้ในโลกแห่งความเป็นจริงเมื่อใด?

ในโลกแห่งความเป็นจริง อัตราส่วนอัตราต่อรองถูกใช้ในบริบทที่หลากหลาย ซึ่งนักวิจัยต้องการเปรียบเทียบโอกาสของเหตุการณ์สองเหตุการณ์ที่เกิดขึ้น นี่คือตัวอย่างบางส่วน.

ตัวอย่าง #1: การตีความอัตราส่วนอัตราต่อรอง

นักวิจัยต้องการทราบว่าการรักษาแบบใหม่ช่วยเพิ่มโอกาสที่ผู้ป่วยจะประสบกับผลลัพธ์ด้านสุขภาพที่เป็นบวกหรือไม่ เมื่อเทียบกับการรักษาที่มีอยู่ ตารางต่อไปนี้แสดงจำนวนผู้ป่วยที่ประสบกับผลลัพธ์ด้านสุขภาพที่เป็นบวกหรือลบ ขึ้นอยู่กับการรักษา

โอกาสที่ผู้ป่วยจะประสบกับผลลัพธ์ที่เป็นบวกจากการรักษาแบบใหม่สามารถคำนวณได้ดังนี้:

โอกาส = P(บวก) / 1 – P(บวก) = (50/90) / 1-(50/90) = (50/90) / (40/90) = 1.25

โอกาสที่ผู้ป่วยจะประสบกับผลลัพธ์ที่เป็นบวกจากการรักษาที่มีอยู่สามารถคำนวณได้ดังนี้:

โอกาส = P(บวก) / 1 – P(บวก) = (42/90) / 1-(42/90) = (42/90) / (48/90) = 0.875

ดังนั้น อัตราต่อรองของการบรรลุผลลัพธ์ที่เป็นบวกด้วยการรักษาใหม่เมื่อเปรียบเทียบกับการรักษาที่มีอยู่ สามารถคำนวณได้ดังนี้:

อัตราต่อรอง = 1.25 / 0.875 = 1.428

เราตีความสิ่งนี้หมายความว่า โอกาสที่คนไข้จะมีผลเป็นบวกจากการรักษาแบบใหม่คือ 1.428 เท่า ของ โอกาส ที่คนไข้จะมีผลบวกจากการรักษาที่มีอยู่

กล่าวอีกนัยหนึ่ง โอกาสในการประสบผลบวกจะเพิ่มขึ้น 42.8% ด้วยการรักษาแบบใหม่

ตัวอย่างที่ 2: การตีความอัตราส่วนอัตราต่อรอง

นักการตลาดต้องการทราบว่าโฆษณาทำให้ลูกค้าซื้อสินค้าที่กำหนดบ่อยกว่าโฆษณาอื่นหรือไม่ ดังนั้นพวกเขาจึงแสดงโฆษณาแต่ละรายการต่อคน 100 คน ตารางต่อไปนี้แสดงจำนวนผู้ที่ซื้อสินค้าโดยอิงตามโฆษณาที่พวกเขาเห็น:

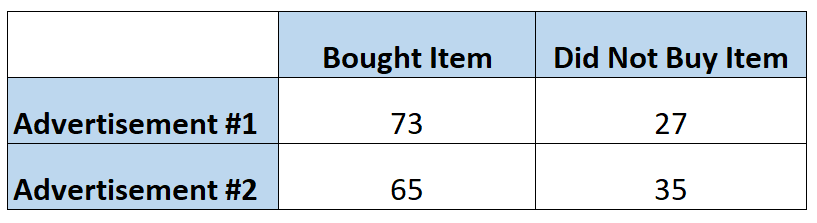
โอกาสที่บุคคลจะซื้อสินค้าหลังจากเห็นโฆษณาแรกสามารถคำนวณได้ดังนี้:

ราคาต่อรอง = P(ซื้อ) / 1 – P(ซื้อ) = (73/100) / 1-(73/100) = (73/100) / (27/100) = 2.704

โอกาสที่บุคคลจะซื้อสินค้าหลังจากเห็นโฆษณาชิ้นที่สองสามารถคำนวณได้ดังนี้:

ราคาต่อรอง = P(ซื้อ) / 1 – P(ซื้อ) = (65/100) / 1-(65/10) = (65/100) / (35/100) = 1.857

ดังนั้น อัตราต่อรองสำหรับลูกค้าที่ซื้อสินค้าหลังจากเห็นโฆษณาแรกเทียบกับการซื้อหลังจากเห็นโฆษณาที่สอง สามารถคำนวณได้ดังนี้:

อัตราต่อรอง = 2.704 / 1.857 = 1.456

เราตีความสิ่งนี้หมายความว่าโอกาสที่บุคคลจะซื้อสินค้าหลังจากเห็นโฆษณาแรกคือ 1.456 เท่า ของโอกาส ที่ บุคคลจะซื้อสินค้าหลังจากเห็นโฆษณาที่สอง

กล่าวอีกนัยหนึ่ง โอกาสในการซื้อสินค้าเพิ่มขึ้น 45.6% จากการลงประกาศครั้งแรก

แหล่งข้อมูลเพิ่มเติม

วิธีการคำนวณอัตราส่วนอัตราต่อรองและความเสี่ยงสัมพัทธ์ใน Excel
วิธีตีความอัตราส่วนอัตราต่อรองที่น้อยกว่า 1
วิธีการตีความความเสี่ยงสัมพัทธ์