ถัวเฉลี่ยถ่วงน้ำหนัก
ที่นี่เราจะอธิบายว่าค่าเฉลี่ยถ่วงน้ำหนักคืออะไรและคำนวณอย่างไร คุณจะสามารถดูแบบฝึกหัดที่แก้ไขได้เกี่ยวกับวิธีการหาค่าเฉลี่ยถ่วงน้ำหนัก และยิ่งไปกว่านั้น คุณยังสามารถคำนวณค่าเฉลี่ยถ่วงน้ำหนักของชุดข้อมูลใดๆ ได้ด้วยเครื่องคิดเลขที่อยู่ตอนท้าย
ค่าเฉลี่ยถ่วงน้ำหนักคืออะไร?
ค่าเฉลี่ยถ่วงน้ำหนักเป็นการวัดความเป็นศูนย์กลางของสถิติเชิงพรรณนา ใน การคำนวณค่าเฉลี่ยถ่วงน้ำหนัก คุณต้องคูณข้อมูลทางสถิติแต่ละรายการด้วยน้ำหนัก (หรือน้ำหนัก) ก่อน จากนั้นจึงบวกผลคูณทั้งหมด และสุดท้ายหารผลรวมถ่วงน้ำหนักด้วยผลรวมของน้ำหนักทั้งหมด
กล่าวอีกนัยหนึ่ง สูตรสำหรับค่าเฉลี่ยถ่วงน้ำหนักมีดังนี้:

โดยที่ x i แสดงถึงตัวอย่างข้อมูลแต่ละตัวอย่าง และ มี น้ำหนักที่สอดคล้องกัน
ดังนั้น ยิ่งข้อมูลมีน้ำหนักมากเท่าใด ข้อมูลก็ยิ่งมีความสำคัญมากขึ้นในการคำนวณค่าเฉลี่ยถ่วงน้ำหนัก กล่าวอีกนัยหนึ่ง ยิ่งการถ่วงน้ำหนักของข้อมูลมีค่ามากเท่าใด ข้อมูลก็จะยิ่งส่งผลต่อผลลัพธ์ของค่าเฉลี่ยถ่วงน้ำหนักมากขึ้นเท่านั้น
ค่าเฉลี่ยถ่วงน้ำหนักมีประโยชน์อย่างยิ่งสำหรับการคำนวณเกรด เนื่องจากช่วยให้คุณสามารถประเมินแบบฝึกหัดหรือการสอบระหว่างหลักสูตรโดยมีความสำคัญต่างกัน ค่าเฉลี่ยถ่วงน้ำหนักยังใช้ในการคำนวณ CPI (ดัชนีราคาผู้บริโภค) ซึ่งเป็นตัวบ่งชี้ในการวัดราคาของประชากร
นอกจากค่าเฉลี่ยถ่วงน้ำหนักแล้ว ยังมีค่าเฉลี่ยประเภทอื่นๆ เช่น ค่าเฉลี่ยเรขาคณิต ค่าเฉลี่ยเลขคณิต ค่าเฉลี่ยกำลังสอง และค่าเฉลี่ยฮาร์มอนิก
วิธีการคำนวณถัวเฉลี่ยถ่วงน้ำหนัก
ในการคำนวณค่าเฉลี่ยถ่วงน้ำหนัก ต้องปฏิบัติตามขั้นตอนต่อไปนี้:
- คูณข้อมูลทางสถิติแต่ละรายการด้วยน้ำหนักที่สอดคล้องกัน
- เพิ่มผลิตภัณฑ์ทั้งหมดที่คำนวณในขั้นตอนก่อนหน้า
- หารผลรวมถ่วงน้ำหนักด้านบนด้วยผลรวมของน้ำหนักทั้งหมด
- ผลลัพธ์ที่ได้คือค่าเฉลี่ยถ่วงน้ำหนักของกลุ่มตัวอย่างทางสถิติ
👉 คุณสามารถใช้เครื่องคิดเลขด้านล่างเพื่อคำนวณค่าเฉลี่ยถ่วงน้ำหนักของชุดข้อมูลใดก็ได้
ตัวอย่างค่าเฉลี่ยถ่วงน้ำหนัก
เมื่อพิจารณาถึงคำจำกัดความของค่าเฉลี่ยถ่วงน้ำหนัก เราจะมาแก้แบบฝึกหัดเพื่อทำความเข้าใจอย่างถ่องแท้ว่าค่าเฉลี่ยถ่วงน้ำหนักได้มาจากชุดข้อมูลอย่างไร
- นักเรียนชั้นมัธยมศึกษาปีที่ 1 ได้เกรดต่อไปนี้ในวิชาคณิตศาสตร์: ข้อสอบบางส่วนได้ 7 คะแนนซึ่งคิดเป็น 30%, งานกลุ่มได้ 9 คะแนนซึ่งมีค่าเท่ากับ 20%, แบบฝึกหัดที่ให้ในชั้นเรียนได้ 6 คะแนนโดยมีการถ่วงน้ำหนัก 10% และ 8 ในการสอบปลายภาคซึ่งมีน้ำหนัก 40% เกรดสุดท้ายของคุณสำหรับวิชานี้คือเท่าไร?
ในการกำหนดคะแนนของนักเรียนคุณต้องค้นหาค่าเฉลี่ยถ่วงน้ำหนักด้วยค่าที่กำหนดโดยคำสั่ง ในการทำเช่นนี้ เราใช้สูตรถัวเฉลี่ยถ่วงน้ำหนัก:
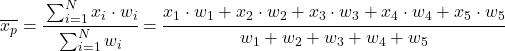
คะแนนของการส่งมอบแต่ละครั้งเป็นมูลค่าทางสถิติ และเปอร์เซ็นต์จะสอดคล้องกับน้ำหนักของมูลค่าดังกล่าว ดังนั้นเราจึงแทนที่ค่าและน้ำหนักลงในสูตรและทำการคำนวณถัวเฉลี่ยถ่วงน้ำหนัก:
![]()
ดังนั้นเกรดคณิตศาสตร์สุดท้ายของนักเรียนคนนี้จึงเท่ากับ 7.7 เพราะนี่คือผลลัพธ์ที่ได้จากค่าเฉลี่ยถ่วงน้ำหนัก
เครื่องคิดเลขถัวเฉลี่ยถ่วงน้ำหนัก
ป้อนข้อมูลจากตัวอย่างทางสถิติและน้ำหนักตามลำดับลงในเครื่องคิดเลขด้านล่างเพื่อคำนวณค่าเฉลี่ยถ่วงน้ำหนัก
ป้อนข้อมูลทางสถิติในช่องแรกและน้ำหนักตามลำดับในช่องที่สอง คุณต้องเขียนน้ำหนักตามลำดับเดียวกันกับข้อมูลและอยู่ในรูปแบบทศนิยม ตัวเลขทั้งหมดจะต้องคั่นด้วยช่องว่างและป้อนโดยใช้จุดเป็นตัวคั่นทศนิยม
ตุ้มน้ำหนักที่ได้มาตรฐาน
ดังที่เราได้เห็นแล้วว่าในค่าเฉลี่ยถ่วงน้ำหนักคือค่าที่มอบให้กับข้อมูลแต่ละชิ้นเพื่อให้ความสำคัญไม่มากก็น้อย ดังนั้นหากข้อมูลมีความสำคัญมากก็จะมีน้ำหนักที่สูงมาก แต่ถ้าข้อมูลไม่เกี่ยวข้องมากนักก็จะมีน้ำหนักที่น้อยมาก
น้ำหนักปกติคือการถ่วงน้ำหนักประเภทหนึ่งที่ใช้หาค่าเฉลี่ยถ่วงน้ำหนักโดยไม่ต้องหารใดๆ
น้ำหนักที่ทำให้เป็นมาตรฐาน คือน้ำหนักของรายการข้อมูลหารด้วยผลรวมของน้ำหนักทั้งหมด
![]()
ผลรวมของน้ำหนักมาตรฐานทั้งหมดจึงเท่ากับหนึ่ง:
![]()
ดังนั้น ใน การคำนวณค่าเฉลี่ยถ่วงน้ำหนักด้วยน้ำหนักที่ทำให้เป็นมาตรฐาน เพียงคูณแต่ละรายการข้อมูลด้วยน้ำหนักที่ทำให้เป็นมาตรฐาน:
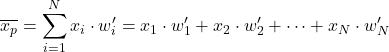
ตัวอย่างเช่น เรามีตัวอย่างทางสถิติซึ่งมีข้อมูลเป็น 24, 35, 17, 41 และน้ำหนักตามลำดับคือ 4, 9, 6, 3 หากต้องการค้นหาค่าเฉลี่ยถ่วงน้ำหนักของชุดข้อมูลนี้ อันดับแรกเราสามารถคำนวณน้ำหนักที่ทำให้เป็นมาตรฐานโดยการหาร แต่ละน้ำหนักด้วยผลรวมของน้ำหนักทั้งหมด:
![]()
![]()
![]()
![]()
และตอนนี้เพียงคูณแต่ละข้อมูลด้วยน้ำหนักปกติแล้วผลลัพธ์จะเป็นค่าเฉลี่ยถ่วงน้ำหนัก:
![]()
ความแตกต่างระหว่างค่าเฉลี่ยถ่วงน้ำหนักและค่าเฉลี่ยเลขคณิต
การคำนวณค่าเฉลี่ยถ่วงน้ำหนักและค่าเฉลี่ยเลขคณิตทำได้ในลักษณะเดียวกัน เนื่องจากจะต้องดำเนินการที่คล้ายกัน ในการเฉลี่ยถ่วงน้ำหนัก จุดข้อมูลแต่ละจุดจะคูณด้วยน้ำหนักและหารด้วยผลรวมของน้ำหนัก แต่ในการเฉลี่ยเลขคณิต ข้อมูลทั้งหมดจะถูกรวมเข้าด้วยกันและหารด้วยจำนวนจุดข้อมูลทั้งหมด
ความแตกต่างระหว่างค่าเฉลี่ยถ่วงน้ำหนักและค่าเฉลี่ยเลขคณิตนั้น อยู่ในแนวคิดของมัน เนื่องจากในค่าเฉลี่ยเลขคณิตถือว่าข้อมูลทั้งหมดมีค่าเท่ากัน อย่างไรก็ตาม ในค่าเฉลี่ยถ่วงน้ำหนัก แต่ละข้อมูลจะมีน้ำหนักต่างกัน
โปรดทราบว่าหากน้ำหนักทั้งหมดเท่ากัน ค่าเฉลี่ยถ่วงน้ำหนักจะเท่ากับค่าเฉลี่ยเลขคณิต คุณสามารถดูการพิสูจน์ทางคณิตศาสตร์ด้านล่าง:
![Rendered by QuickLaTeX.com \begin{aligned}\overline{x_p}&=\cfrac{x_1\cdot w+x_2\cdot w+x_3\cdot w+\dots+x_N\cdot w}{w+w+w+\dots +w}\\[2ex]&= \cfrac{w\cdot (x_1+x_2+\dots+x_N)}{N\cdot w}=\\[2ex] &= \cfrac{x_1+x_2+\dots+x_N}{N}=\overline{x}\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-16b06cfb0813f7f4fd755ea7bbf1bf00_l3.png)