วิธีทำการทดสอบ chow ใน python
การทดสอบ Chow ใช้เพื่อทดสอบว่าค่าสัมประสิทธิ์ของแบบจำลองการถดถอยที่แตกต่างกันสองชุดในชุดข้อมูลที่ต่างกันเท่ากันหรือไม่
โดยทั่วไปการทดสอบนี้จะใช้ในด้านเศรษฐมิติด้วยข้อมูลอนุกรมเวลาเพื่อพิจารณาว่าข้อมูลมีการแบ่งแยกทางโครงสร้าง ณ จุดใดเวลาหนึ่งหรือไม่
ตัวอย่างทีละขั้นตอนต่อไปนี้แสดงวิธีดำเนินการทดสอบ Chow ใน Python
ขั้นตอนที่ 1: สร้างข้อมูล
ขั้นแรก เราจะสร้างข้อมูลปลอม:
import pandas as pd #createDataFrame df = pd. DataFrame ({' x ': [1, 1, 2, 3, 4, 4, 5, 5, 6, 7, 7, 8, 8, 9, 10, 10, 11, 12, 12, 13, 14, 15, 15, 16, 17, 18, 18, 19, 20, 20], ' y ': [3, 5, 6, 10, 13, 15, 17, 14, 20, 23, 25, 27, 30, 30, 31, 33, 32, 32, 30, 32, 34, 34, 37, 35, 34, 36, 34, 37, 38, 36]}) #view first five rows of DataFrame df. head () x y 0 1 3 1 1 5 2 2 6 3 3 10 4 4 13
ขั้นตอนที่ 2: แสดงภาพข้อมูล
ต่อไป เราจะสร้าง Scatterplot แบบง่ายๆ เพื่อแสดงข้อมูลเป็นภาพ:
import matplotlib. pyplot as plt
#create scatterplot
plt. plot (df. x , df. y , ' o ')
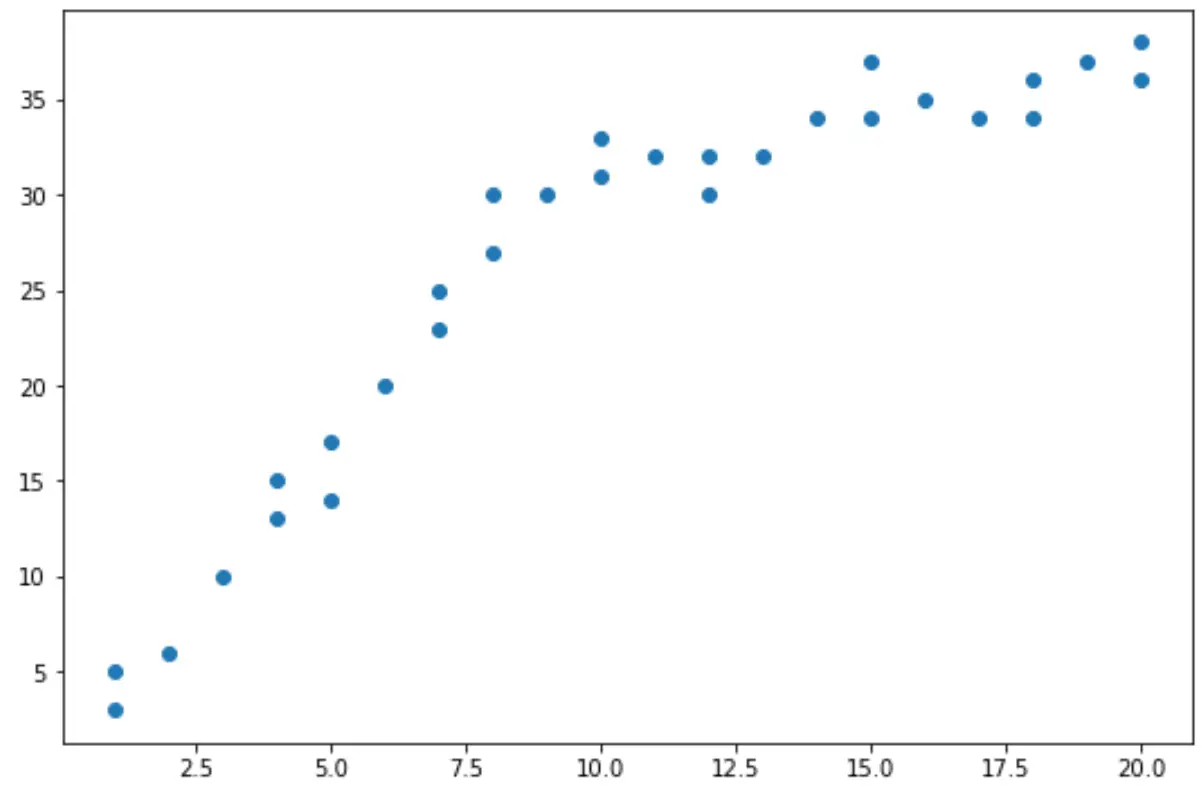
จากแผนภาพกระจาย เราจะเห็นว่าแนวโน้มของข้อมูลมีการเปลี่ยนแปลงที่ x = 10
ดังนั้นเราจึงสามารถทำการทดสอบ Chow เพื่อพิจารณาว่ามีจุดพักเชิงโครงสร้างในข้อมูลที่ x = 10 หรือไม่
ขั้นตอนที่ 3: ทำการทดสอบ Chow
เราสามารถใช้ฟังก์ชัน chowtest ของแพ็คเกจ chowtest ใน Python เพื่อทำการทดสอบ Chow
ก่อนอื่น เราต้องติดตั้งแพ็คเกจนี้โดยใช้ pip:
pip install chowtest
จากนั้นเราสามารถใช้ไวยากรณ์ต่อไปนี้เพื่อทำการทดสอบ Chow:
from chow_test import chowtest chowtest ( y=df[[' y ']], last_index_in_model_1= 15 , first_index_in_model_2= 16 , significance_level= .05 ) ************************************************** ********************************* Reject the null hypothesis of equality of regression coefficients in the 2 periods. ************************************************** ********************************* Chow Statistic: 118.14097335479373 p value: 0.0 ************************************************** ********************************* (118.14097335479373, 1.1102230246251565e-16)
ต่อไปนี้คือความหมายของแต่ละอาร์กิวเมนต์ในฟังก์ชัน chowtest() :
- y : ตัวแปรตอบสนองใน DataFrame
- x : ตัวแปรทำนายใน DataFrame
- Last_index_in_model_1 : ค่าดัชนีของจุดสุดท้ายก่อนการแตกโครงสร้าง
- first_index_in_model_2 : ค่าดัชนีสำหรับจุดแรกหลังจากการแตกโครงสร้าง
- นัยสำคัญ_ระดับ : ระดับนัยสำคัญที่จะใช้สำหรับการทดสอบสมมติฐาน
จากผลการทดสอบเราจะเห็นได้ว่า:
- สถิติ การทดสอบ F : 118.14
- ค่า p: <.0000
เนื่องจากค่า p น้อยกว่า 0.05 เราจึงสามารถปฏิเสธสมมติฐานว่างของการทดสอบได้ ซึ่งหมายความว่าเรามีหลักฐานเพียงพอที่จะบอกว่ามีเบรกพอยต์เชิงโครงสร้างอยู่ในข้อมูล
กล่าวอีกนัยหนึ่ง เส้นการถดถอยสองเส้นสามารถใส่แบบจำลองในข้อมูลได้อย่างมีประสิทธิภาพมากกว่าเส้นการถดถอยเส้นเดียว
แหล่งข้อมูลเพิ่มเติม
บทช่วยสอนต่อไปนี้จะอธิบายวิธีดำเนินการทดสอบทั่วไปอื่นๆ ใน Python:
วิธีการทดสอบ Granger Causality ใน Python
วิธีทำการทดสอบ Breusch-Pagan ใน Python
วิธีทำการทดสอบของ White ใน Python