วิธีทำให้ข้อมูลเป็นมาตรฐานใน excel

หากต้องการ “ทำให้เป็นมาตรฐาน” ชุดของค่าข้อมูลหมายถึงการปรับขนาดค่าดังกล่าวโดยค่าเฉลี่ยของค่าทั้งหมดคือ 0 และค่าเบี่ยงเบนมาตรฐานคือ 1

บทช่วยสอนนี้จะอธิบายวิธีการทำให้ข้อมูลเป็นมาตรฐานใน Excel

ตัวอย่าง: วิธีทำให้ข้อมูลเป็นมาตรฐานใน Excel

สมมติว่าเรามีชุดข้อมูลต่อไปนี้ใน Excel:

ทำตามขั้นตอนต่อไปนี้เพื่อทำให้ชุดข้อมูลนี้เป็นมาตรฐาน

ขั้นตอนที่ 1: ค้นหาค่าเฉลี่ย

ขั้นแรก เราจะใช้ฟังก์ชัน =AVERAGE(ช่วงของค่า) เพื่อค้นหาค่าเฉลี่ยของชุดข้อมูล

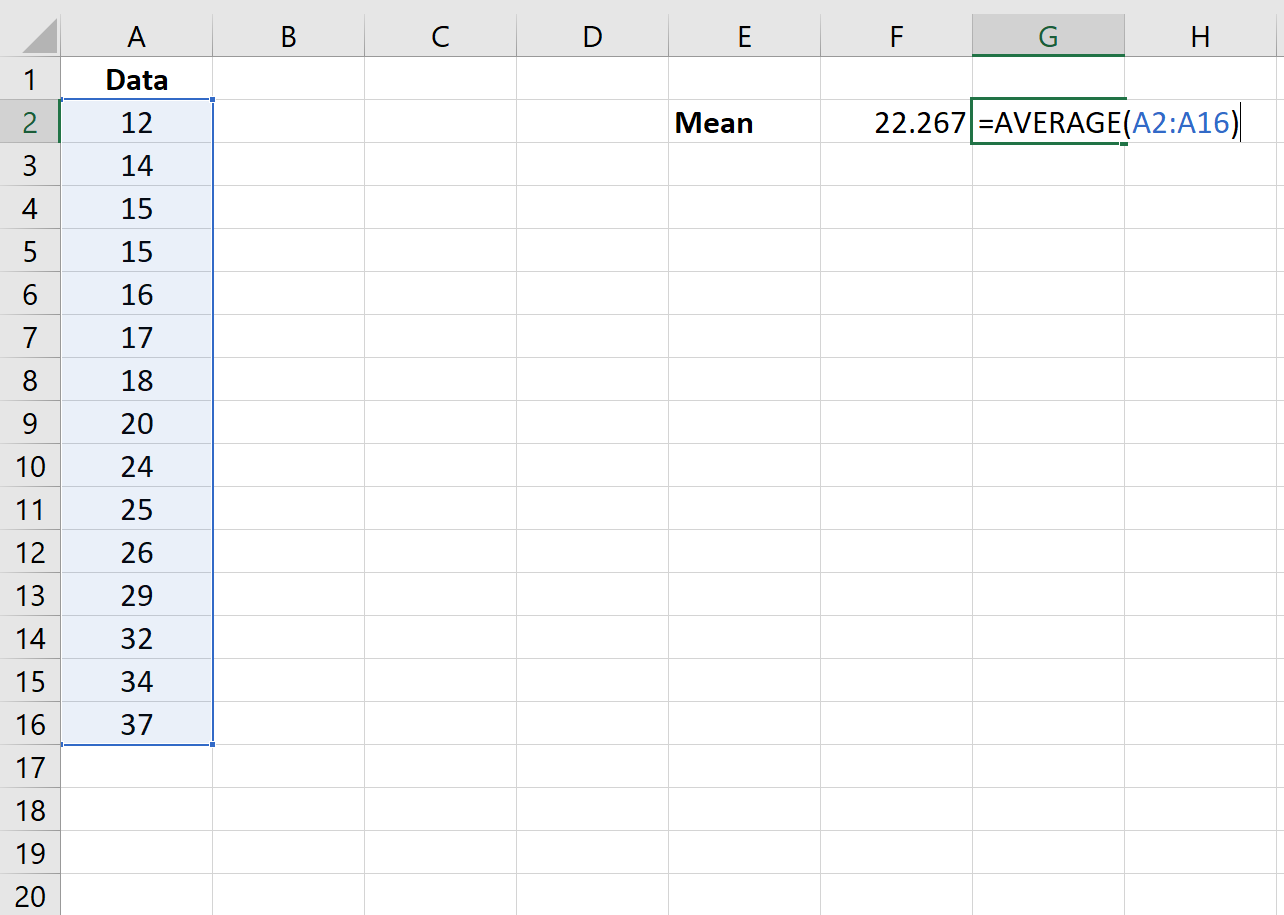
ขั้นตอนที่ 2: ค้นหาส่วนเบี่ยงเบนมาตรฐาน

ต่อไป เราจะใช้ฟังก์ชัน =STDEV (ช่วงของค่า) เพื่อค้นหาค่าเบี่ยงเบนมาตรฐานของชุดข้อมูล

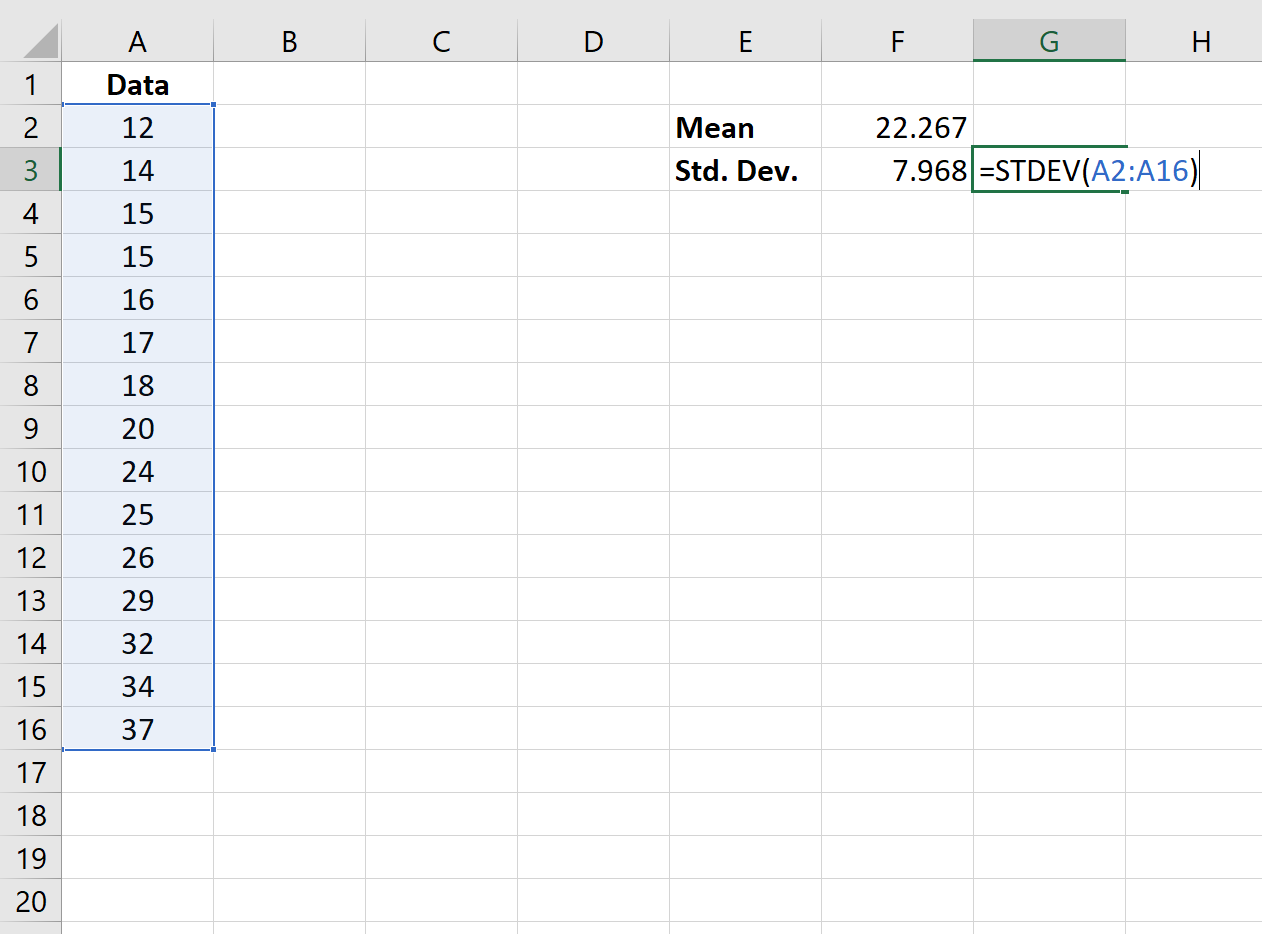
ขั้นตอนที่ 3: ทำให้ค่าเป็นมาตรฐาน

สุดท้ายนี้ เราจะใช้ฟังก์ชัน STANDARDIZE(x, Mean, standard_dev) เพื่อทำให้ค่าแต่ละค่าในชุดข้อมูลเป็นมาตรฐาน

บันทึก:

ฟังก์ชัน STANDARDIZE ใช้สูตรต่อไปนี้เพื่อทำให้ค่าข้อมูลที่กำหนดเป็นมาตรฐาน:

ค่าปกติ = (x – x ) / s

ทอง:

• x = ค่าข้อมูล
• x = ค่าเฉลี่ยของชุดข้อมูล
• s = ส่วนเบี่ยงเบนมาตรฐานของชุดข้อมูล

รูปภาพต่อไปนี้แสดงสูตรที่ใช้ในการทำให้ค่าแรกในชุดข้อมูลเป็นมาตรฐาน:

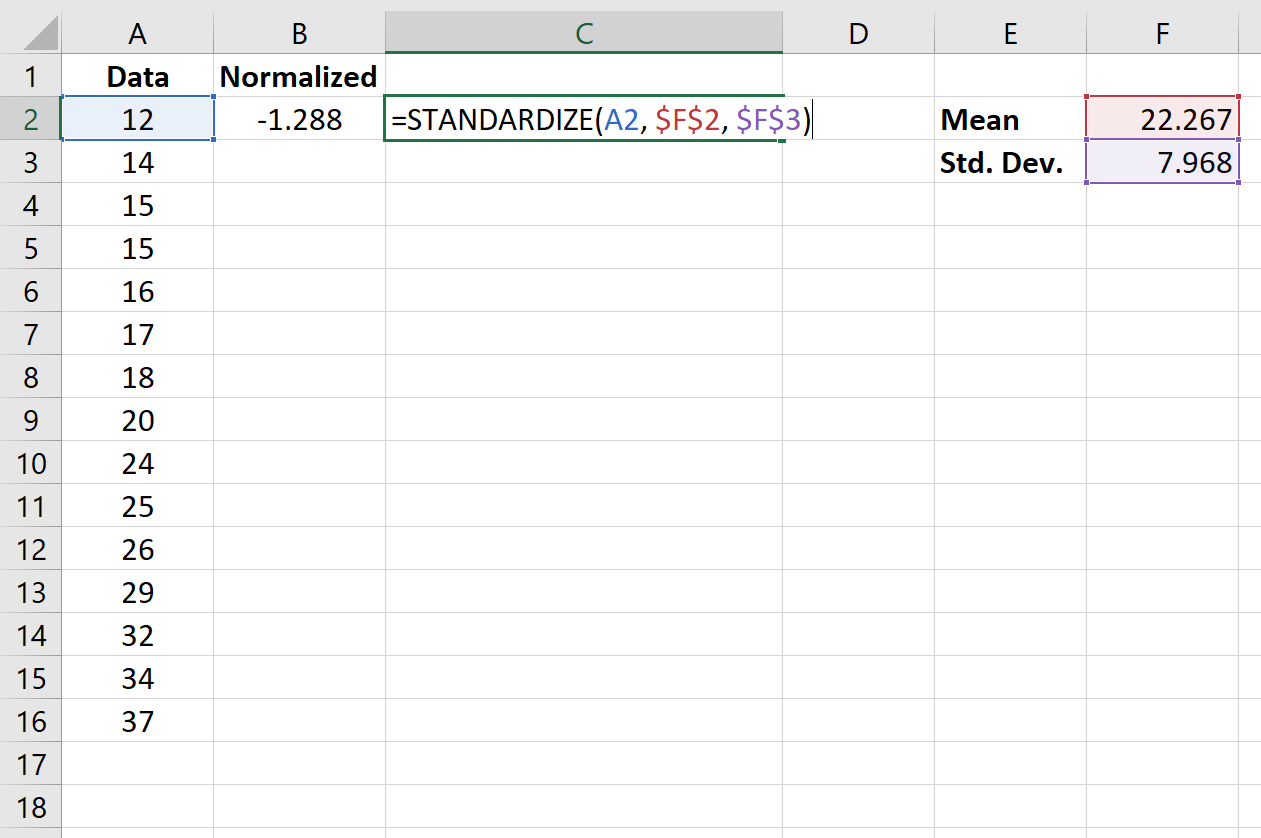
เมื่อเราทำให้ค่าแรกในเซลล์ B2 เป็นมาตรฐานแล้ว เราก็สามารถเลื่อนเมาส์ไปที่มุมขวาล่างของเซลล์ B2 จนกระทั่งเครื่องหมาย + เล็กปรากฏขึ้น ดับเบิลคลิก + เพื่อคัดลอกสูตรไปยังเซลล์ที่เหลือ:

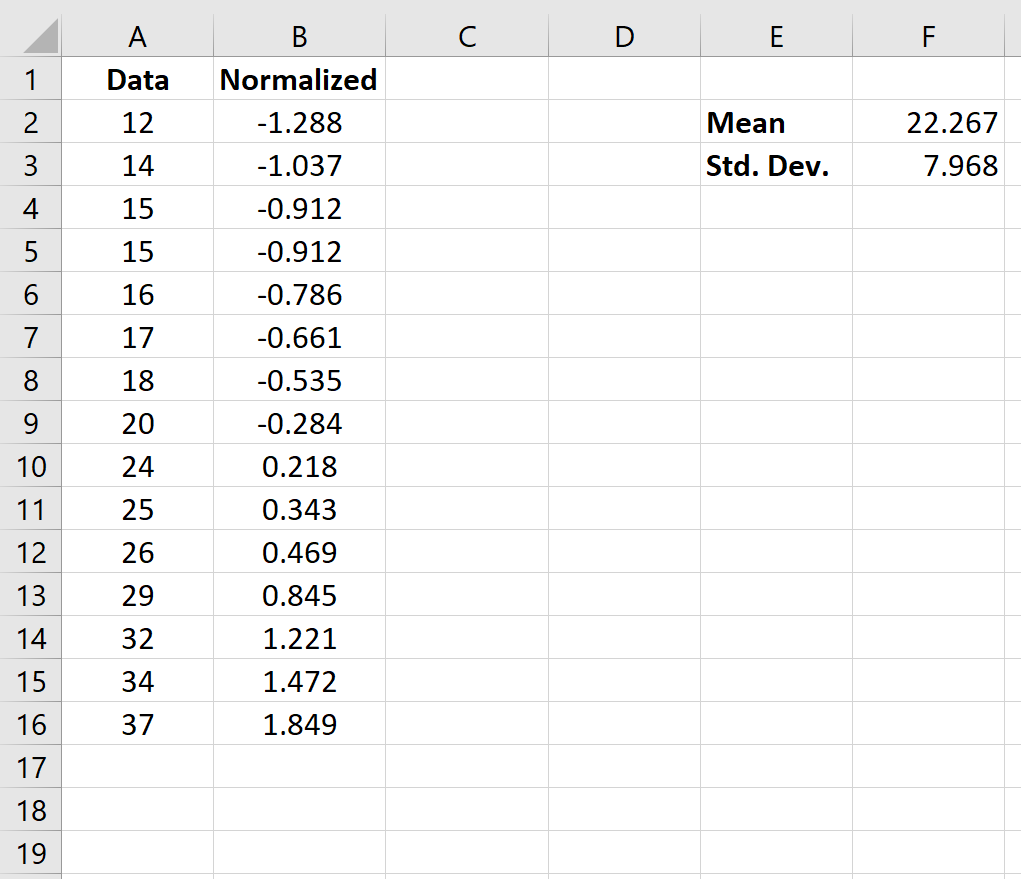
ตอนนี้ทุกค่าในชุดข้อมูลจะถูกทำให้เป็นมาตรฐาน

วิธีการตีความข้อมูลที่ทำให้เป็นมาตรฐาน

สูตรที่เราใช้เพื่อทำให้ค่าข้อมูลที่กำหนด x เป็นมาตรฐานคือ:

ค่าปกติ = (x – x ) / s

ทอง:

• x = ค่าข้อมูล
• x = ค่าเฉลี่ยของชุดข้อมูล
• s = ส่วนเบี่ยงเบนมาตรฐานของชุดข้อมูล

หากจุดข้อมูลใดจุดหนึ่งมีค่าที่ทำให้เป็นมาตรฐานมากกว่า 0 แสดงว่าจุดข้อมูลนั้นสูงกว่าค่าเฉลี่ย ในทางกลับกัน ค่าที่ทำให้เป็นมาตรฐานที่น้อยกว่า 0 บ่งชี้ว่าจุดข้อมูลต่ำกว่าค่าเฉลี่ย

โดยเฉพาะอย่างยิ่ง ค่าที่ทำให้เป็นมาตรฐานจะบอกเราว่าจุดข้อมูลเดิมนั้นมีค่าเบี่ยงเบนมาตรฐานเป็นจำนวนเท่าใดจากค่าเฉลี่ย ตัวอย่างเช่น พิจารณาจุดข้อมูล “12” ในชุดข้อมูลดั้งเดิมของเรา:

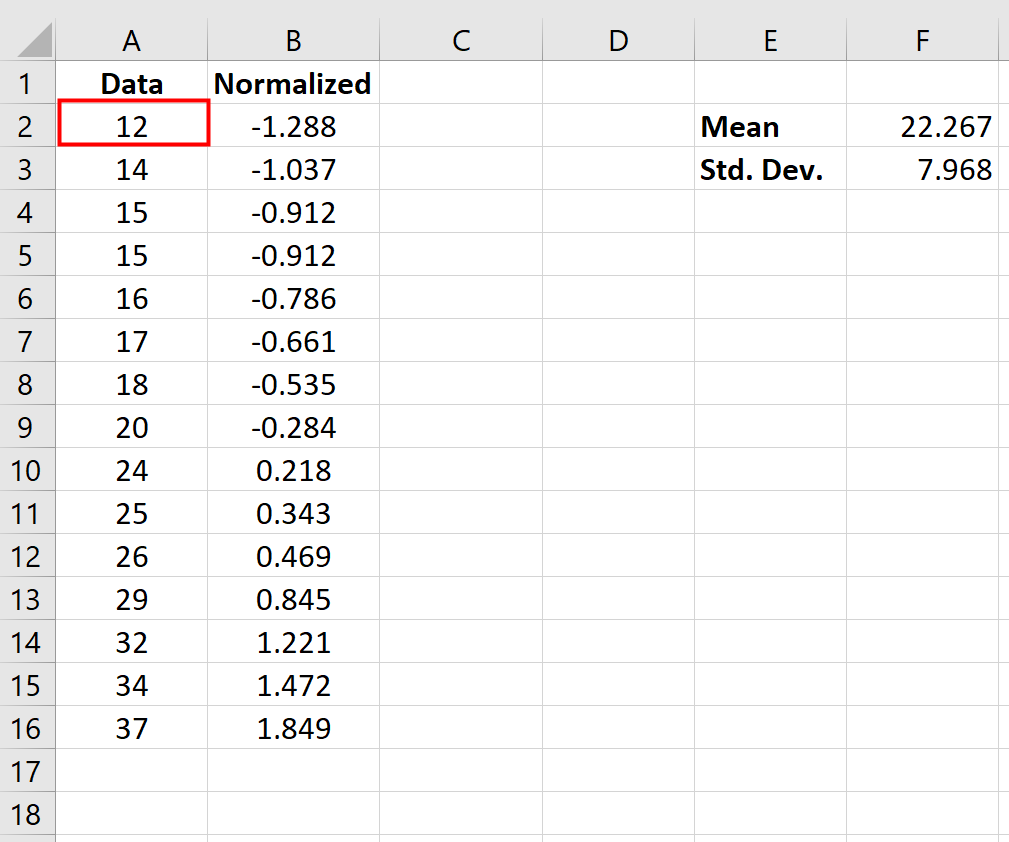
ค่าปกติของ “12” กลายเป็น -1.288 ซึ่งคำนวณได้ดังนี้:

ค่าปกติ = (x – x ) / s = (12 – 22.267) / 7.968 = -1.288

สิ่งนี้บอกเราว่าค่า “12” คือ ค่าเบี่ยงเบนมาตรฐาน 1.288 ซึ่งต่ำกว่าค่าเฉลี่ย ของชุดข้อมูลดั้งเดิม

ค่ามาตรฐานแต่ละค่าในชุดข้อมูลสามารถช่วยให้เราเข้าใจว่าค่าข้อมูลเฉพาะนั้นอยู่ห่างจากค่าเฉลี่ยมากน้อยเพียงใด ค่าที่ทำให้เป็นมาตรฐานเล็กน้อยบ่งชี้ว่าค่านั้นใกล้เคียงกับค่าเฉลี่ย ในขณะที่ค่าที่ทำให้เป็นมาตรฐานขนาดใหญ่บ่งชี้ว่าค่านั้นอยู่ไกลจากค่าเฉลี่ย