บทนำโดยย่อเกี่ยวกับการตรวจสอบความถูกต้องแบบ cross-one-out (loocv)

ในการประเมินประสิทธิภาพของแบบจำลองในชุดข้อมูล เราจำเป็นต้องวัดว่าการคาดการณ์ที่ทำโดยแบบจำลองนั้นตรงกับข้อมูลที่สังเกตได้ดีเพียงใด

วิธีที่พบบ่อยที่สุดในการวัดนี้คือการใช้ค่าคลาดเคลื่อนกำลังสองเฉลี่ย (MSE) ซึ่งคำนวณได้ดังนี้:

MSE = (1/n)*Σ(y _i – f(x _i )) ²

ทอง:

• n: จำนวนการสังเกตทั้งหมด
• y _i : ค่าตอบสนองของการสังเกต ^{ครั้งที่ 3}
• f(x _i ): ค่าตอบสนองที่คาดการณ์ไว้ของการสังเกต ^{ครั้ง} ที่ i

ยิ่งการคาดการณ์แบบจำลองใกล้กับการสังเกตมากเท่าไร MSE ก็จะยิ่งต่ำลงเท่านั้น

ในทางปฏิบัติ เราใช้กระบวนการต่อไปนี้ในการคำนวณ MSE ของแบบจำลองที่กำหนด:

1. แบ่งชุดข้อมูลออกเป็นชุดการฝึกและชุดทดสอบ

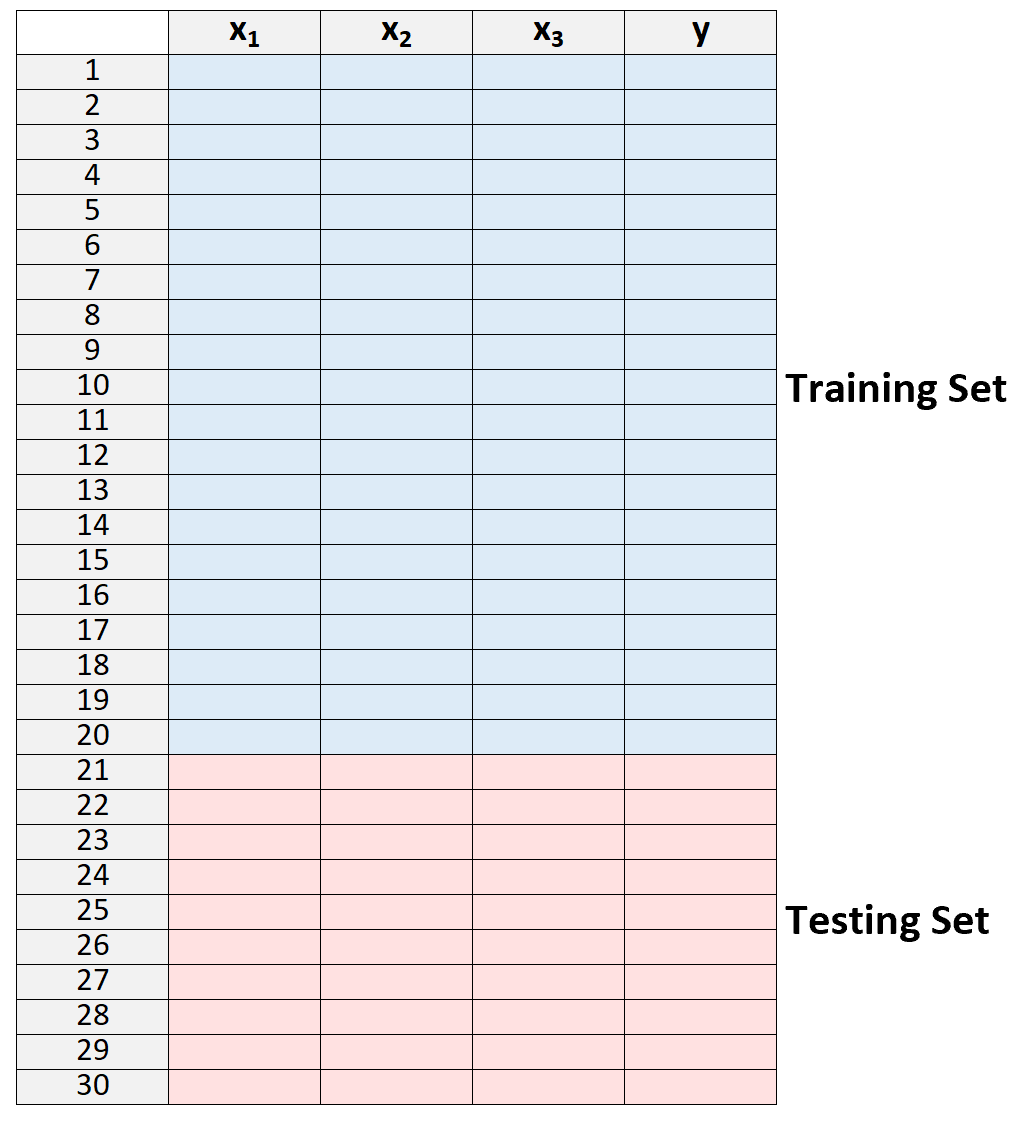
2. สร้างแบบจำลองโดยใช้ข้อมูลจากชุดการฝึกเท่านั้น

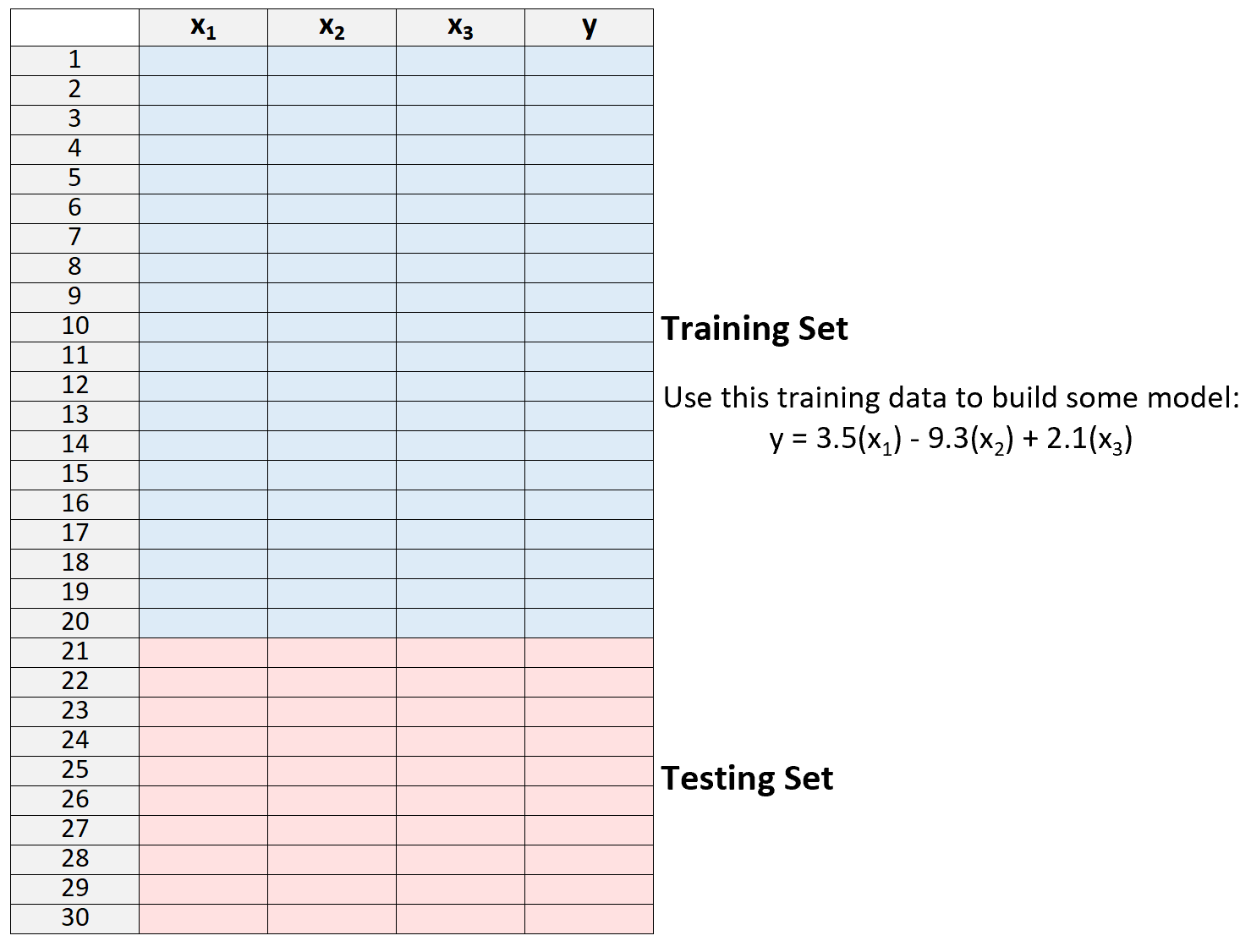
3. ใช้แบบจำลองเพื่อคาดการณ์เกี่ยวกับชุดทดสอบและวัด MSE ซึ่งเรียกว่า test MSE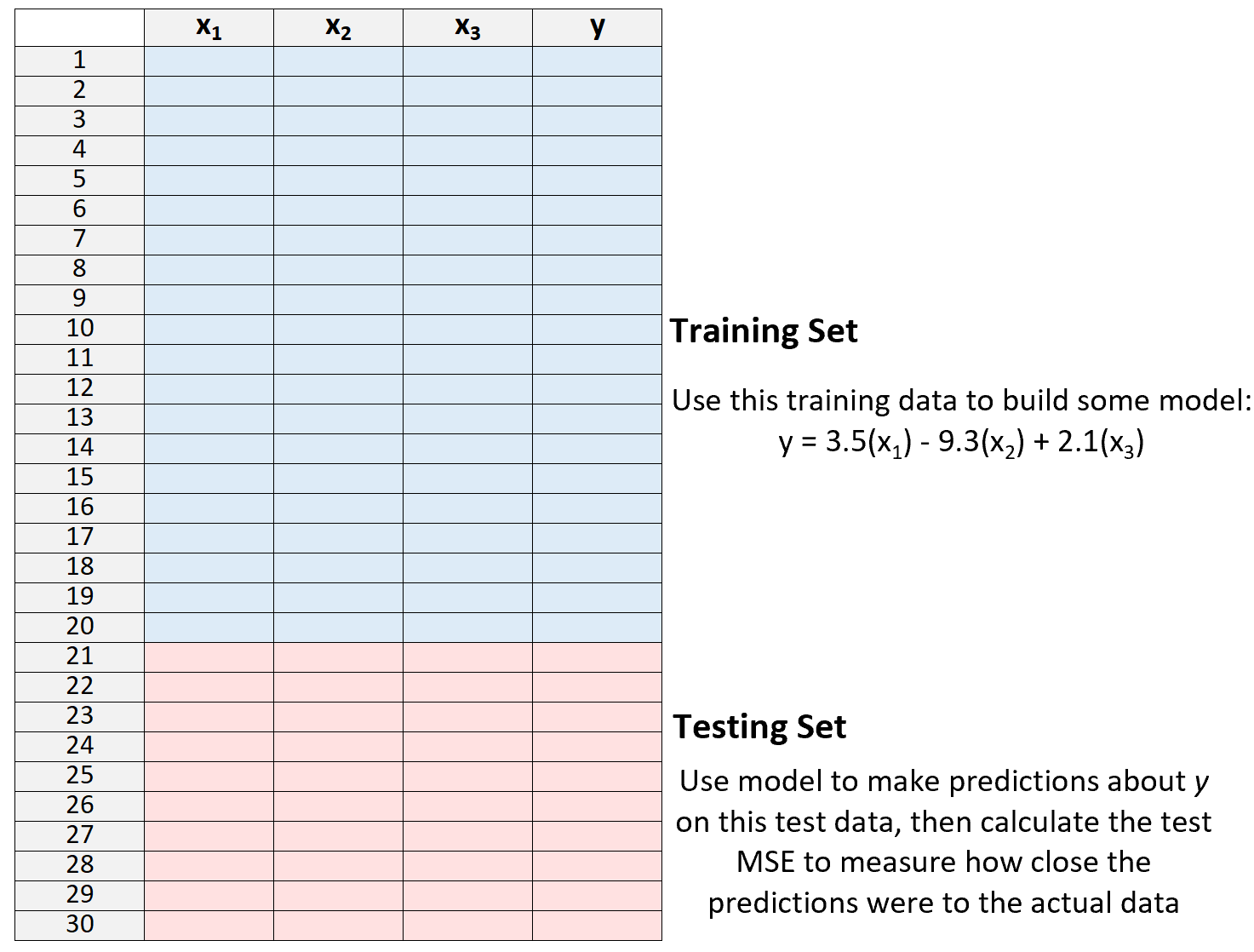

การทดสอบ MSE ช่วยให้เราทราบว่าโมเดลทำงานได้ดีเพียงใดกับข้อมูลที่ไม่เคยเห็นมาก่อน ซึ่งก็คือข้อมูลที่ยังไม่เคยใช้ในการ “ฝึก” โมเดล

อย่างไรก็ตาม ข้อเสียของการใช้ชุดทดสอบชุดเดียวก็คือ การทดสอบ MSE อาจแตกต่างกันอย่างมาก ขึ้นอยู่กับข้อสังเกตที่ใช้ในชุดการฝึกและชุดทดสอบ

เป็นไปได้ว่าหากเราใช้ชุดการสังเกตที่แตกต่างกันสำหรับชุดการฝึกและชุดการทดสอบ การทดสอบ MSE ของเราอาจมีขนาดใหญ่กว่าหรือเล็กกว่ามาก

วิธีหนึ่งในการหลีกเลี่ยงปัญหานี้คือการปรับโมเดลให้เหมาะสมหลายครั้งโดยใช้ชุดการฝึกและการทดสอบที่แตกต่างกันในแต่ละครั้ง จากนั้นคำนวณ MSE การทดสอบเป็นค่าเฉลี่ยของ MSE การทดสอบทั้งหมด

วิธีการทั่วไปนี้เรียกว่าการตรวจสอบความถูกต้องแบบข้าม และรูปแบบเฉพาะเรียกว่า การตรวจสอบความถูกต้องแบบข้ามแบบออกครั้งเดียว

การตรวจสอบข้ามแบบลาออกครั้งเดียว

การตรวจสอบความถูกต้องข้ามแบบละเว้น ใช้วิธีการต่อไปนี้เพื่อประเมินแบบจำลอง:

1. แบ่งชุดข้อมูลออกเป็นชุดการฝึกและชุดทดสอบ โดยใช้การสังเกตทั้งหมดยกเว้นชุดเดียวเป็นส่วนหนึ่งของชุดการฝึก:

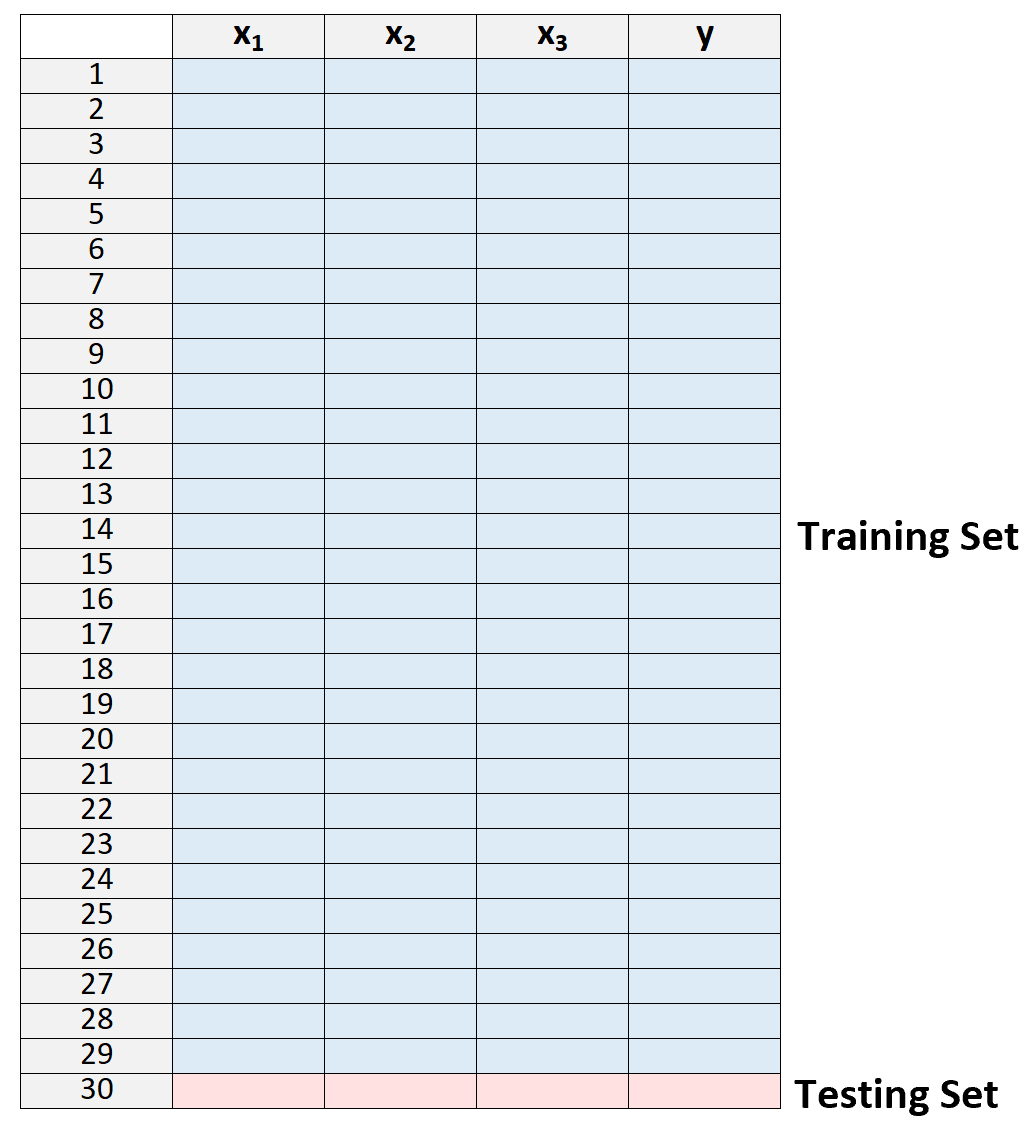
โปรดทราบว่าเราจะทิ้งข้อสังเกตไว้เพียง “นอก” ชุดการฝึกเท่านั้น นี่คือที่วิธีการได้รับชื่อการตรวจสอบข้ามแบบ “leave-one-out”

2. สร้างแบบจำลองโดยใช้ข้อมูลจากชุดการฝึกเท่านั้น

3. ใช้แบบจำลองเพื่อทำนายค่าการตอบสนองของการสังเกตเดี่ยวที่ไม่รวมอยู่ในแบบจำลองและคำนวณ MSE

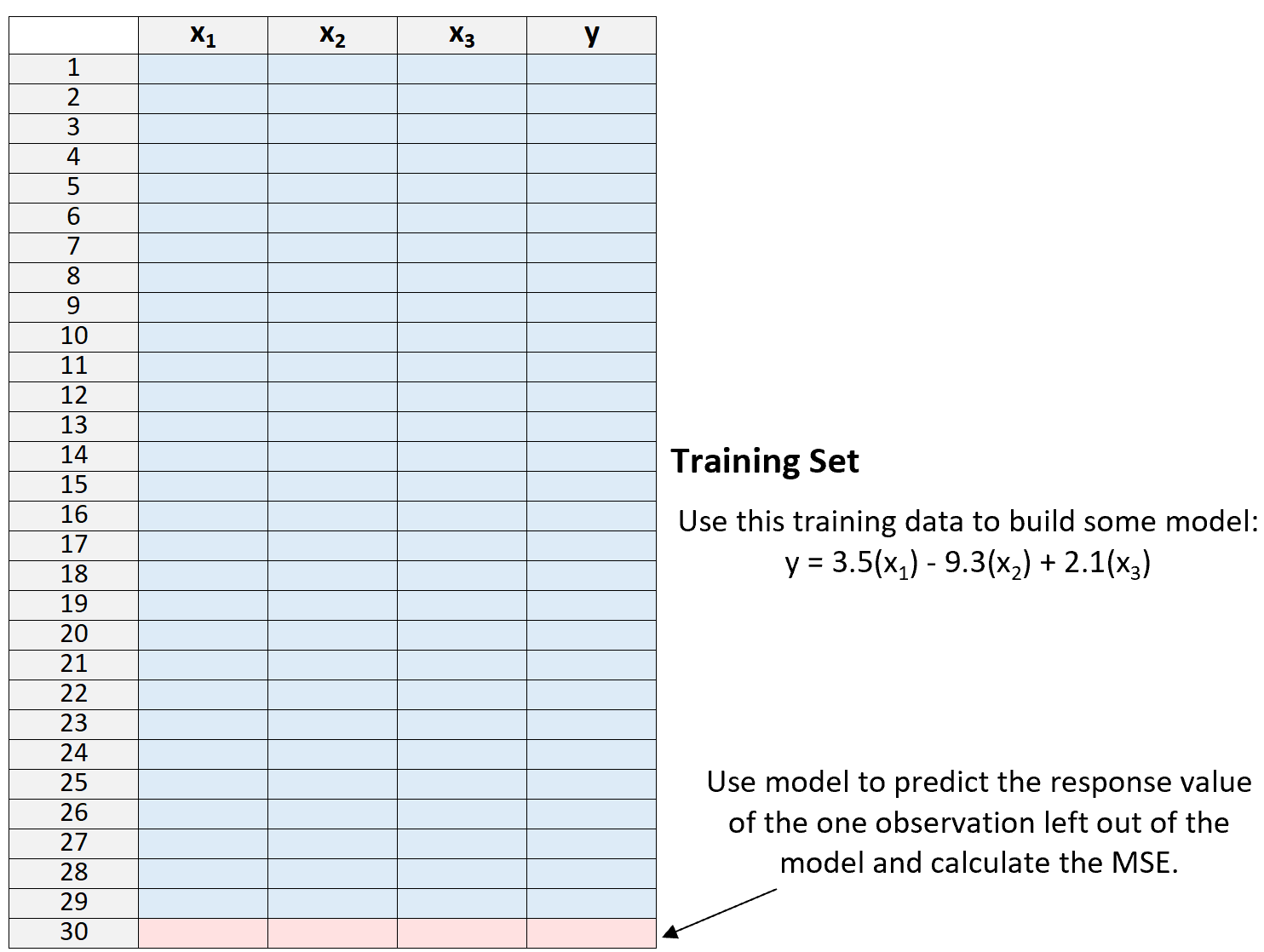
4. ทำซ้ำขั้นตอนนี้ n ครั้ง

สุดท้าย เราทำซ้ำขั้นตอนนี้ n ครั้ง (โดยที่ n คือจำนวนการสังเกตทั้งหมดในชุดข้อมูล) โดยละเว้นการสังเกตที่แตกต่างจากชุดการฝึกในแต่ละครั้ง

จากนั้นเราจะคำนวณ MSE ทดสอบเป็นค่าเฉลี่ยของ MSE ทดสอบทั้งหมด:

การทดสอบ MSE = (1/n)*ΣMSE _i

ทอง:

• n: จำนวนการสังเกตทั้งหมดในชุดข้อมูล
• MSEi: การทดสอบ MSE ระหว่างช่วงระยะเวลาการลองโมเดล ^{ที่ 3}

ข้อดีและข้อเสียของ LOOCV

การตรวจสอบความถูกต้องข้ามแบบละเว้นจะให้ ประโยชน์ ดังต่อไปนี้:

• ซึ่งให้การวัดการทดสอบ MSE ที่มีอคติน้อยกว่ามากเมื่อเทียบกับการใช้ชุดการทดสอบเดียว เนื่องจากเราปรับแบบจำลองให้เข้ากับชุดข้อมูลที่มีการสังเกต n-1 ซ้ำๆ
• มีแนวโน้มที่จะไม่ประเมินค่า MSE ของการทดสอบสูงเกินไป เมื่อเทียบกับการใช้ชุดทดสอบชุดเดียว

อย่างไรก็ตาม การตรวจสอบข้ามแบบแฮนด์ออฟมี ข้อเสียดังต่อไปนี้:

• การใช้กระบวนการนี้อาจใช้เวลานานเมื่อ n มีขนาดใหญ่
• นอกจากนี้ยังอาจใช้เวลานานหากโมเดลมีความซับซ้อนเป็นพิเศษและใช้เวลานานในการติดตั้งชุดข้อมูล
• อาจมีราคาแพงในการคำนวณ

โชคดีที่คอมพิวเตอร์ยุคใหม่มีประสิทธิภาพในด้านส่วนใหญ่จนทำให้ LOOCV เป็นวิธีการใช้งานที่สมเหตุสมผลมากกว่าเมื่อหลายปีก่อนมาก

โปรดทราบว่า LOOCV สามารถใช้ในบริบท การถดถอยและการจำแนก ประเภทได้ สำหรับปัญหาการถดถอย ระบบจะคำนวณการทดสอบ MSE เป็นค่าความแตกต่างรากกำลังสองเฉลี่ยระหว่างการทำนายและการสังเกต ในขณะที่ปัญหาการจำแนกประเภท จะคำนวณการทดสอบ MSE เป็นเปอร์เซ็นต์ของการสังเกตที่จำแนกอย่างถูกต้องในการปรับเปลี่ยนแบบจำลองซ้ำ n ครั้ง

วิธีรัน LOOCV ใน R & Python

บทช่วยสอนต่อไปนี้ให้ตัวอย่างทีละขั้นตอนเกี่ยวกับวิธีการรัน LOOCV สำหรับโมเดลที่กำหนดใน R และ Python:

การตรวจสอบความถูกต้องแบบ Cross-One-Out ใน R
การตรวจสอบความถูกต้องแบบ Cross-One-Out ใน Python