พล็อตกระจาย

บทความนี้จะอธิบายว่าแผนกระจายคืออะไร ดังนั้น คุณจะค้นพบว่า Point Cloud ใช้ทำอะไร วิธีสร้าง Point Cloud วิธีตีความ และตัวอย่าง Point Cloud

พอยต์คลาวด์คืออะไร?

Scatterplot หรือ Scatterplot เป็นแผนภาพทางสถิติประเภทหนึ่งซึ่งชุดข้อมูลของตัวแปรสองตัวจะถูกสร้างกราฟบนแกนพิกัดคาร์ทีเซียนสองแกน

ดังนั้นจึงใช้แผนกระจายเพื่อวิเคราะห์ความสัมพันธ์ระหว่างตัวแปรทางสถิติสองตัว

Scatterplot มีชื่อที่แตกต่างกันหลายชื่อ เช่น แผนภาพสหสัมพันธ์ หรือ Scatterplot

ควรสังเกตว่าแผนภาพกระจายถือเป็นหนึ่งในเครื่องมือพื้นฐานของการควบคุมคุณภาพ เช่นเดียวกับแผนภูมิ Pareto แผนภาพสาเหตุและผลกระทบ ผังงาน ฯลฯ

วิธีสร้างพล็อตกระจาย

หากต้องการ สร้างแผนภูมิกระจาย คุณต้องทำตามขั้นตอนต่อไปนี้:

1. รวบรวมข้อมูลทางสถิติจากตัวอย่างที่คุณต้องการวิเคราะห์ โปรดทราบว่าในการสร้างแผนภูมิกระจาย ต้องมีตัวแปรเชิงปริมาณอย่างน้อยสองตัว
2. พล็อตสองแกนของพล็อตกระจาย
3. กำหนดตัวแปรทางสถิติสองตัวที่จะนำมาสร้างเป็นกราฟ
4. ปรับเทียบมาตราส่วนของแต่ละแกนของกราฟ ในการดำเนินการนี้ ขอแนะนำให้ค้นหาค่าต่ำสุดและค่าสูงสุดของตัวแปรแต่ละตัวก่อน แล้วจึงปรับขนาดแต่ละแกนตามค่าเหล่านี้
5. แทนข้อมูลแต่ละคู่บนแผนภาพกระจายด้วยจุด
6. วิเคราะห์และตีความแผนภาพกระจายที่ได้รับ

ตัวอย่างแผนภูมิกระจาย

หลังจากได้เห็นคำจำกัดความของแผนภาพกระจายและทฤษฎีการสร้างแล้ว ในส่วนนี้จะนำเสนอแผนภาพประเภทนี้เป็นตัวอย่าง

• ในตารางความถี่ต่อไปนี้ จะรวบรวมคะแนนคณิตศาสตร์และสถิติของกลุ่มตัวอย่างนักเรียน 20 คนเป็นข้อมูล พล็อตชุดข้อมูลบน Scatterplot แล้ววิเคราะห์

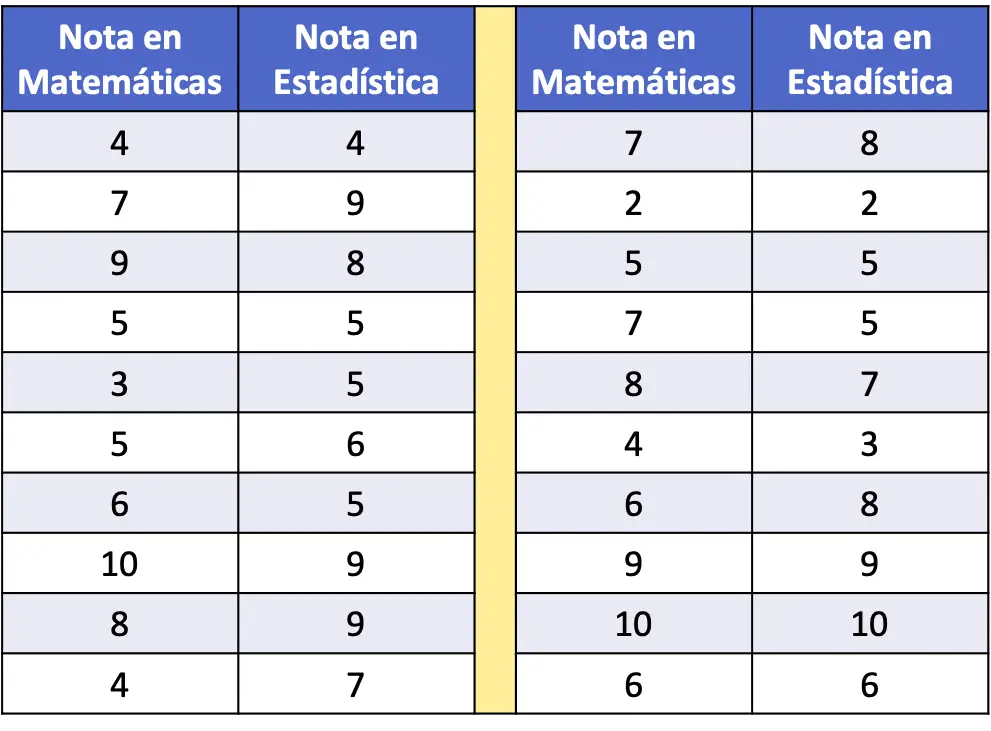
ในการแสดงชุดข้อมูลในรูปแบบกระจาย เราเพียงแค่ต้องพล็อตสองแกน ปรับเทียบแกนเหล่านั้น และพล็อตจุดบนกราฟสำหรับข้อมูลแต่ละคู่ โปรดจำไว้ว่าจุดบนกราฟจะถูกวางไว้ที่จุดตัดของเส้นจินตภาพซึ่งสอดคล้องกับค่าแต่ละค่าของมัน

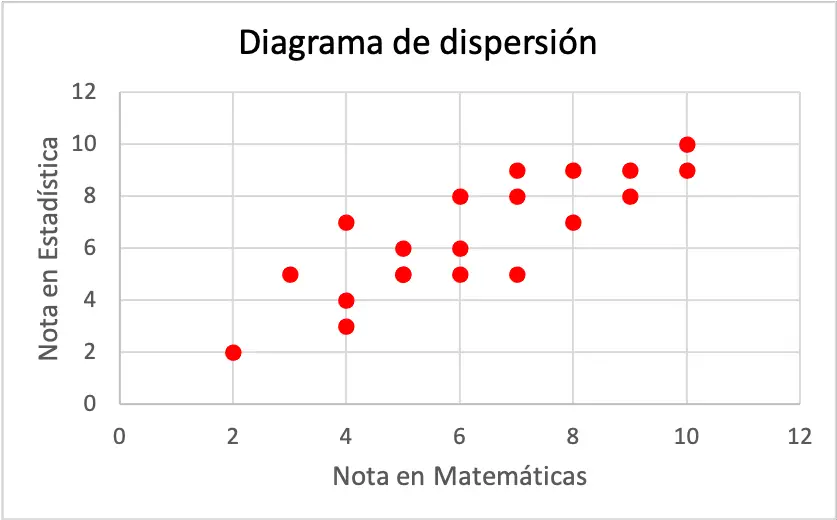
แต่ละแกนของแผนภูมิกระจายแสดงถึงตัวแปร แม่นยำยิ่งขึ้นแกนนอนเป็นของเกรดที่ได้รับในวิชาคณิตศาสตร์และในทางกลับกันแกนตั้งนั้นสอดคล้องกับเกรดที่ได้รับในสถิติ

ดังที่คุณเห็นจากแผนภาพกระจาย ตัวแปรทั้งสองมีความสัมพันธ์เชิงบวก เนื่องจากตัวแปรตัวหนึ่งเพิ่มขึ้นเมื่อตัวแปรอีกตัวหนึ่งเพิ่มขึ้นเช่นกัน ดังนั้นจึงสรุปได้ว่าหากนักเรียนได้เกรดดีขึ้นในวิชาคณิตศาสตร์ ก็มีแนวโน้มว่าเขาหรือเธอจะได้เกรดดีขึ้นในวิชาสถิติด้วย และในทางกลับกัน

อย่างไรก็ตาม ข้อสรุปก่อนหน้านี้ไม่ได้หมายความว่าตัวแปรตัวหนึ่งเป็นสาเหตุของอีกตัวแปรหนึ่ง เนื่องจากการได้เกรดดีในวิชาคณิตศาสตร์ไม่ได้รับประกันว่าจะได้เกรดดีในวิชาสถิติโดยอัตโนมัติโดยไม่ต้องทำอะไรเลย แต่ควรเรียนทั้งสองวิชามากกว่า ในส่วนถัดไป เราจะอธิบายรายละเอียดเพิ่มเติมเกี่ยวกับแนวคิดนี้

โครงเรื่องกระจายและความสัมพันธ์

จากแผนภาพกระจาย สามารถระบุประเภทของความสัมพันธ์ระหว่างตัวแปรสองตัวได้:

• ความสัมพันธ์โดยตรง (หรือความสัมพันธ์เชิงบวก) : ตัวแปรหนึ่งจะเพิ่มขึ้นเมื่ออีกตัวแปรหนึ่งเพิ่มขึ้นเช่นกัน
• ความสัมพันธ์แบบผกผัน (หรือความสัมพันธ์เชิงลบ) : เมื่อตัวแปรตัวหนึ่งเพิ่มขึ้น อีกตัวหนึ่งก็จะลดลง และในทางกลับกัน หากตัวแปรตัวหนึ่งลดลง อีกตัวก็จะเพิ่มขึ้น
• Zero correlation (No correlation) : ไม่มีความสัมพันธ์ระหว่างตัวแปรทั้งสอง

ในทำนองเดียวกัน ไม่ว่าความสัมพันธ์ระหว่างตัวแปรทั้งสองจะเป็นแบบตรงหรือแบบผกผัน ความสัมพันธ์ก็สามารถจำแนกตามจุดแข็งหรือจุดอ่อนของความสัมพันธ์ระหว่างตัวแปรทั้งสองได้

• ความสัมพันธ์ที่แข็งแกร่ง: ตัวแปรทั้งสองมีความเชื่อมโยงกันอย่างใกล้ชิด จุดต่างๆ จะถูกนำมารวมกันบนพอยต์คลาวด์ ทำให้ระบุความสัมพันธ์ระหว่างตัวแปรได้ง่ายขึ้น
• ความสัมพันธ์ต่ำ : มีความสัมพันธ์ระหว่างตัวแปรทั้งสอง แต่ยากที่จะระบุ จุดต่างๆ อยู่ไกลกันบนพอยต์คลาวด์

ในทางกลับกัน ความสัมพันธ์ยังสามารถคำนวณเป็นตัวเลขได้โดยใช้สูตร ซึ่งช่วยให้คุณทราบทางคณิตศาสตร์ได้ว่าตัวแปรสองตัวที่ต่างกันมีความสัมพันธ์กันอย่างใกล้ชิดเพียงใด หากต้องการดูวิธีการทำงาน คลิกลิงก์ต่อไปนี้:

โปรดทราบว่าแม้ว่าจะมีความสัมพันธ์กันระหว่างตัวแปรสองตัว แต่ก็ไม่ได้หมายความว่ามีสาเหตุระหว่างตัวแปรทั้งสอง กล่าวคือ ความสัมพันธ์ระหว่างตัวแปรสองตัวไม่ได้หมายความว่าการเปลี่ยนแปลงในตัวแปรตัวหนึ่งเป็นสาเหตุของการเปลี่ยนแปลงในตัวแปรอีกตัวหนึ่ง ตัวแปร.

ดังนั้น เช่นเดียวกับแผนภูมิกระจายในส่วนที่แล้ว แม้ว่าจะมีความสัมพันธ์เชิงบวกระหว่างเกรดคณิตศาสตร์และเกรดสถิติ แต่การได้เกรดที่ดีในวิชาคณิตศาสตร์ไม่ได้หมายความว่าจะได้เกรดที่ดีในวิชาสถิติ เพราะถ้าคุณเรียนแต่วิชาคณิตศาสตร์เท่านั้น คุณจะล้มเหลวอย่างแน่นอน ในสถิติ ดังนั้นตัวแปรทั้งสองจึงมีความสัมพันธ์กันแต่ไม่ใช่เหตุและผล

หากต้องการข้อมูลเพิ่มเติม คุณสามารถดำเนินการต่อในโพสต์ต่อไปนี้:

ข้อดีและข้อเสียของพอยต์คลาวด์

เนื่องจากลักษณะของแผนภูมิกระจาย แผนภูมิสถิติประเภทนี้จึงมีข้อดีและข้อเสีย

ข้อได้เปรียบ:

• มันค่อนข้างง่ายที่จะแสดงชุดข้อมูลบนแผนภูมิกระจาย
• แผนภูมิกระจายช่วยให้คุณวิเคราะห์ความสัมพันธ์ระหว่างตัวแปร 2 ตัวด้วยภาพได้ ทำให้สรุปผลได้ง่ายขึ้น
• Scatterplots สามารถใช้ในการศึกษาทางสถิติเชิงลึกเป็นการสำรวจข้อมูลเบื้องต้นได้

ข้อเสีย:

• ไดอะแกรมประเภทนี้ไม่มีประโยชน์ในการแสดงตัวแปรเชิงคุณภาพ
• การตีความแผนภาพกระจายสามารถนำไปสู่การสรุปสาเหตุและผลกระทบที่ผิดพลาดระหว่างตัวแปรสองตัวได้
• Scatterplots ไม่อนุญาตให้คุณวิเคราะห์ความสัมพันธ์ระหว่างตัวแปรมากกว่าสองตัว