วิธีการคำนวณช่วงระหว่างควอไทล์ (iqr) ใน excel
บทช่วยสอนนี้จะอธิบายวิธีคำนวณ ช่วงระหว่างควอไทล์ ของชุดข้อมูลใน Excel
พิสัยระหว่างควอไทล์คืออะไร?
ช่วง ระหว่างควอไทล์ หรือที่มักเรียกว่า IQR เป็นวิธีการวัดการกระจายตัวของชุดข้อมูลที่อยู่ตรงกลาง 50% โดยคำนวณเป็นความแตกต่างระหว่างควอไทล์แรก* (Q1) และควอไทล์ที่สาม (Q3) ของชุดข้อมูล
*ควอไทล์เป็นเพียงค่าที่แบ่งชุดข้อมูลออกเป็นสี่ส่วนเท่าๆ กัน
ตัวอย่างเช่น สมมติว่าเรามีชุดข้อมูลต่อไปนี้:
[58, 66, 71, 73, 74, 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98]
ควอไทล์ที่สามกลายเป็น 91 และควอไทล์แรกคือ 75.5 ดังนั้น ช่วงระหว่างควอไทล์ (IQR) สำหรับชุดข้อมูลนี้คือ 91 – 75.5 = 15 สิ่งนี้บอกเราถึงการกระจายของค่าตรงกลาง 50% ในชุดข้อมูลนี้
วิธีการคำนวณช่วงระหว่างควอไทล์ใน Excel
Microsoft Excel ไม่มีฟังก์ชันในตัวสำหรับคำนวณ IQR ของชุดข้อมูล แต่เราสามารถค้นหาได้อย่างง่ายดายโดยใช้ฟังก์ชัน QUARTILE() ซึ่งรับอาร์กิวเมนต์ต่อไปนี้:
QUARTILE(อาร์เรย์, ไตรมาส)
- array: อาร์เรย์ข้อมูลที่คุณสนใจ
- ควอร์ต: ควอร์ไทล์ที่คุณต้องการคำนวณ
ตัวอย่าง: การค้นหา IQR ใน Excel
สมมติว่าเราต้องการค้นหา IQR สำหรับชุดข้อมูลต่อไปนี้:
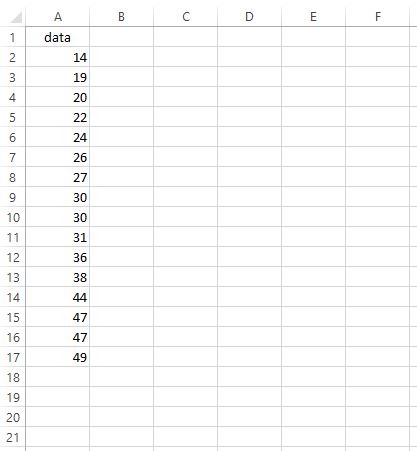
หากต้องการค้นหา IQR เราสามารถทำตามขั้นตอนต่อไปนี้:
ขั้นตอนที่ 1: ค้นหา Q1
หากต้องการค้นหาควอไทล์แรก เพียงพิมพ์ =QUARTILE(A2:A17, 1) ลงในเซลล์ใดก็ได้ที่เราต้องการ:
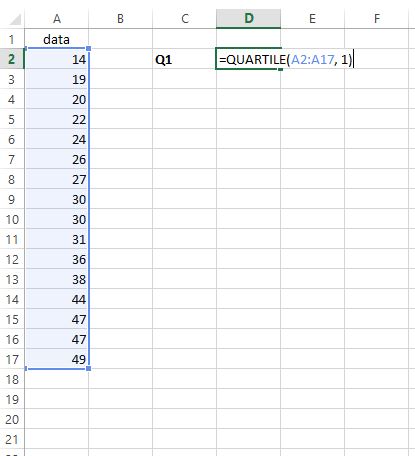
ขั้นตอนที่ 2: ค้นหา Q3
หากต้องการค้นหาควอไทล์ที่สาม ให้พิมพ์ =QUARTILE(A2:A17, 3) ในเซลล์ใดก็ได้ที่เราต้องการ:
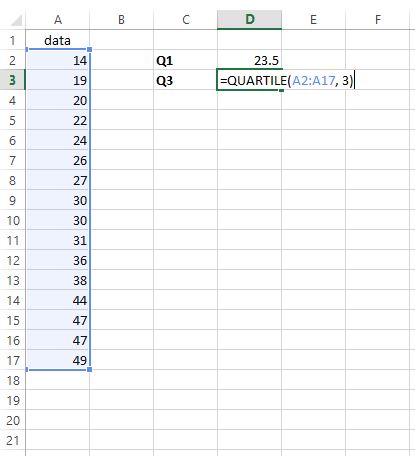
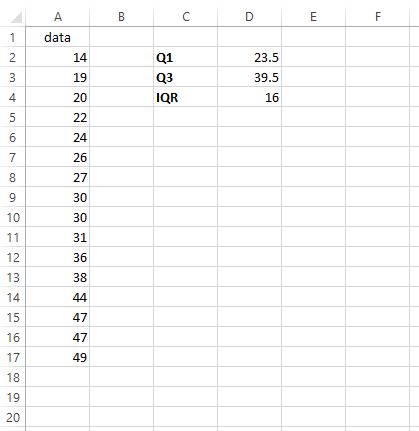
ขั้นตอนที่ 3: ค้นหา IQR
ในการหาพิสัยระหว่างควอไทล์ (IQR) เราเพียงลบ Q1 ออกจาก Q3:
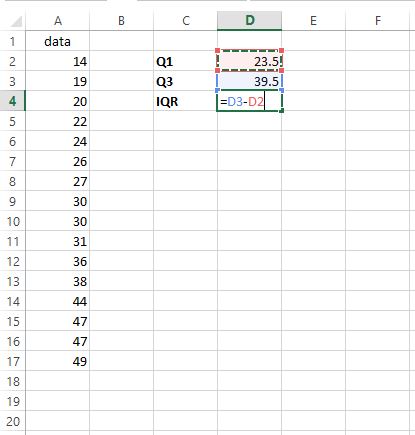
IQR กลายเป็น 39.5 – 23.5 = 16 สิ่งนี้บอกเราว่าค่ากลาง 50% กระจายอยู่ในชุดข้อมูลนี้อย่างไร
แนวทางที่สั้นกว่า
โปรดทราบว่าเราอาจพบช่วงระหว่างควอไทล์ของชุดข้อมูลในตัวอย่างก่อนหน้านี้โดยใช้สูตร:
=ควอไทล์(A2:A17, 3) – ควอไทล์(A2:A17, 1)
สิ่งนี้จะให้ค่า 16 ด้วย
บทสรุป
ช่วงระหว่างควอไทล์เป็นเพียงวิธีหนึ่งในการวัด “การแพร่กระจาย” ของชุดข้อมูล วิธีอื่นๆ ในการวัดค่าสเปรดคือ ช่วง ค่าเบี่ยงเบนมาตรฐาน และความแปรปรวน
ข้อดีของการใช้ IQR เพื่อวัดค่าสเปรดคือ มีความทนทานต่อค่าผิดปกติ เนื่องจากมันบอกเราเพียงการกระจายของชุดข้อมูลตรงกลาง 50% เท่านั้น จึงไม่ได้รับผลกระทบจากค่าผิดปกติที่เล็กหรือใหญ่ผิดปกติ
วิธีนี้ทำให้เป็นวิธีที่ดีกว่าในการวัดการกระจายตัวเมื่อเทียบกับช่วงแบบเมตริก ซึ่งเพียงบอกเราถึงความแตกต่างระหว่างค่าที่ใหญ่ที่สุดและน้อยที่สุดในชุดข้อมูล
ที่เกี่ยวข้อง: วิธีการคำนวณระดับกลางใน Excel