วิธีคำนวณค่าคาดหวังของ x^3
สำหรับ ตัวแปรสุ่ม ซึ่งแสดงด้วย X คุณสามารถใช้สูตรต่อไปนี้เพื่อคำนวณค่าที่คาดหวังของ X 3 :
E(X 3 ) = Σx 3 * พี(x)
ทอง:
- Σ : สัญลักษณ์ที่หมายถึง “ผลรวม”
- x : ค่าของตัวแปรสุ่ม
- p(x) : ความน่าจะเป็นที่ตัวแปรสุ่มรับค่าที่กำหนด
ตัวอย่างต่อไปนี้แสดงวิธีการใช้สูตรนี้ในทางปฏิบัติ
ตัวอย่าง: การคำนวณค่าที่คาดหวังของ X 3
สมมติว่าเรามีตารางการแจกแจงความน่าจะเป็นต่อไปนี้ซึ่งอธิบายความน่าจะเป็นที่ตัวแปรสุ่ม
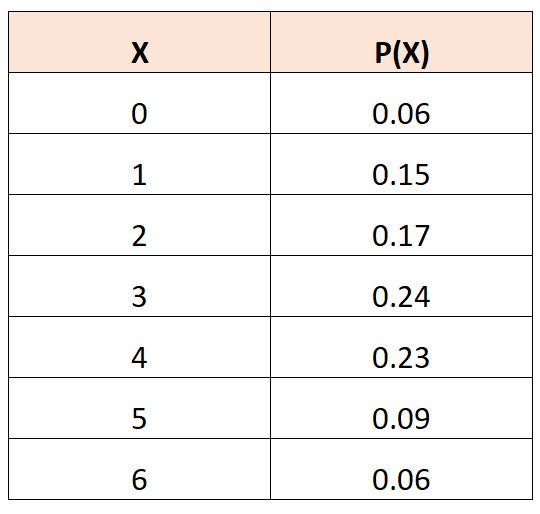
ในการคำนวณค่าที่คาดหวังของ X 3 เราสามารถใช้สูตรต่อไปนี้:
E(X 3 ) = Σx 3 * พี(x)
อี(X 3 ) = (0) 3 *.06 + (1) 3 *.15 + (2) 3 *.17 + (3) 3 *.24 + (4) 3 *.23 + (5) 3 *.09 + (6) 3 *.06
อี(X 3 ) = 0 + 0.15 + 0.1.36 + 6.48 + 14.72 + 11.25 + 12.96
อี(X 3 ) = 45.596
ค่าคาดหวังของ X 3 คือ 45,596
โปรดทราบว่าตัวแปรสุ่มนี้เป็น ตัวแปรสุ่มแบบไม่ต่อเนื่อง ซึ่งหมายความว่าตัวแปรสุ่มสามารถรับค่าได้เพียงจำนวนจำกัดเท่านั้น
ถ้า X เป็น ตัวแปรสุ่มต่อเนื่อง เราต้องใช้สูตรต่อไปนี้เพื่อคำนวณค่าที่คาดหวังของ X 3 :
E(X 3 ) = ∫ x 3 f(x)dx
ทอง:
- ∫: สัญลักษณ์ที่หมายถึง “บูรณาการ”
- f(x) : ไฟล์ pdf ดำเนินต่อไปสำหรับตัวแปรสุ่ม
เมื่อคำนวณมูลค่าที่คาดหวัง ของ
แหล่งข้อมูลเพิ่มเติม
บทช่วยสอนต่อไปนี้จะอธิบายวิธีการทำงานทั่วไปอื่นๆ ในสถิติ:
วิธีค้นหาค่าเฉลี่ยของการแจกแจงความน่าจะเป็น
วิธีค้นหาค่าเบี่ยงเบนมาตรฐานของการแจกแจงความน่าจะเป็น
วิธีค้นหาความแปรปรวนของการแจกแจงความน่าจะเป็น