ลอเรนซ์โค้ง

บทความนี้จะอธิบายว่าเส้นโค้ง Lorenz คืออะไร และใช้เพื่ออะไร คุณจะค้นพบวิธีสร้างเส้นโค้ง Lorenz ของประชากร และนอกจากนี้ คุณจะสามารถดูแบบฝึกหัดที่ได้รับการแก้ไขทีละขั้นตอน ในที่สุด คุณสมบัติของเส้นโค้ง Lorenz และความสัมพันธ์กับดัชนี Gini จะถูกนำเสนอ

เส้นโค้ง Lorenz คืออะไร?

เส้นโค้งลอเรนซ์ คือการแสดงภาพกราฟิกของความไม่เท่าเทียมกันทางเศรษฐกิจของประชากรในดินแดนหนึ่งๆ กล่าวอีกนัยหนึ่ง เส้นโค้งลอเรนซ์เป็นเส้นโค้งที่ช่วยให้เราสามารถวิเคราะห์ความไม่เท่าเทียมกันในการกระจายรายได้เหนืออาณาเขต

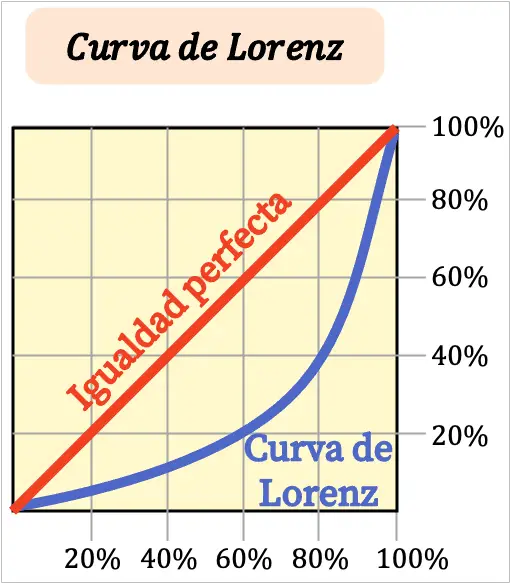
ยิ่งเส้นโค้งลอเรนซ์ตรงเท่าไร รายได้ของดินแดนก็จะยิ่งมีความเท่าเทียมมากขึ้นเท่านั้น ในทางกลับกัน ยิ่งเส้นโค้ง Lorenz โค้งมากเท่าไร การกระจายรายได้ก็จะยิ่งไม่เท่ากันมากขึ้นเท่านั้น

โดยปกติแล้ว แกนของเส้นโค้ง Lorenz จะแสดงเป็นเปอร์เซ็นต์ แกน X ของกราฟแสดงถึงเปอร์เซ็นต์ของประชากร ในทางกลับกัน แกน Y จะแสดงเปอร์เซ็นต์รายได้

เส้นโค้งลอเรนซ์ถูกประดิษฐ์ขึ้นในปี 1905 โดยแม็กซ์ ออตโต ลอเรนซ์ นักเศรษฐศาสตร์ชาวอเมริกันคนสำคัญมากแห่งศตวรรษที่ 20

วิธีการคำนวณเส้นโค้งลอเรนซ์

เมื่อเราทราบคำจำกัดความของเส้นโค้งลอเรนซ์แล้ว เราจะมาดูกันว่าเส้นโค้งทางสถิตินี้คำนวณอย่างไร ควรสังเกตว่ามีสูตรสำหรับกำหนดเส้นโค้ง Lorenz แต่ในทางปฏิบัติโดยทั่วไปไม่ได้ใช้ นั่นเป็นเหตุผลที่เราจะแก้ตัวอย่างทีละขั้นตอนเพื่อให้คุณเห็นว่ามันเสร็จสิ้นอย่างไร

• แสดงถึงเส้นโค้ง Lorenz ของประชากรที่มีรายได้แสดงในตารางต่อไปนี้:

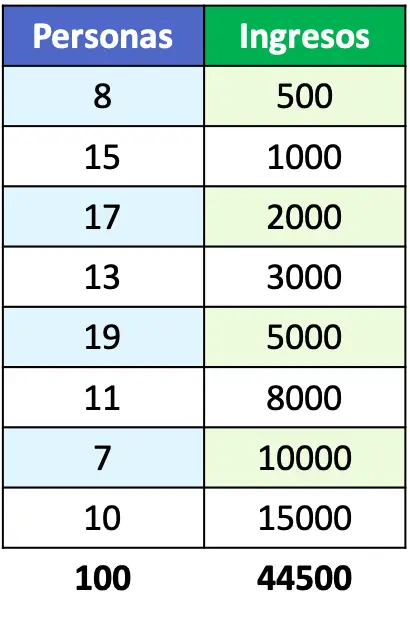
หากข้อความปัญหาให้ตัวอย่างฟังก์ชันเส้นโค้งลอเรนซ์ เราก็สามารถแสดงฟังก์ชันบนกราฟได้โดยตรง แต่ในกรณีนี้ มันบอกแค่รายได้ประชากร เราจึงต้องคำนวณเปอร์เซ็นต์ของคนแต่ละกลุ่ม

ดังนั้น เพื่อกำหนดเปอร์เซ็นต์ของจำนวนคนและรายได้ เราต้องเพิ่มสองคอลัมน์ลงในตารางสำหรับตัวแปรประชากร:

• คอลัมน์ที่มีความถี่สัมบูรณ์สะสม (F _i )
• คอลัมน์ที่สองซึ่งสอดคล้องกับเปอร์เซ็นต์สะสม ซึ่งคำนวณโดยการหารความถี่สัมบูรณ์สะสมด้วยจำนวนคนทั้งหมด

ในทางกลับกัน เราต้องเพิ่มสามคอลัมน์สำหรับตัวแปรรายได้:

• คอลัมน์ที่ใช้คำนวณรายได้รวม เท่ากับผลคูณของจำนวนคนด้วยรายได้ที่แต่ละคนได้รับ
• วินาทีที่มีความถี่สัมบูรณ์สะสม (F _i ) ของรายได้ทั้งหมด
• คอลัมน์ที่สามซึ่งรวมถึงเปอร์เซ็นต์สะสม ซึ่งกำหนดโดยการหารคอลัมน์ก่อนหน้าด้วยรายได้รวมของประชากร

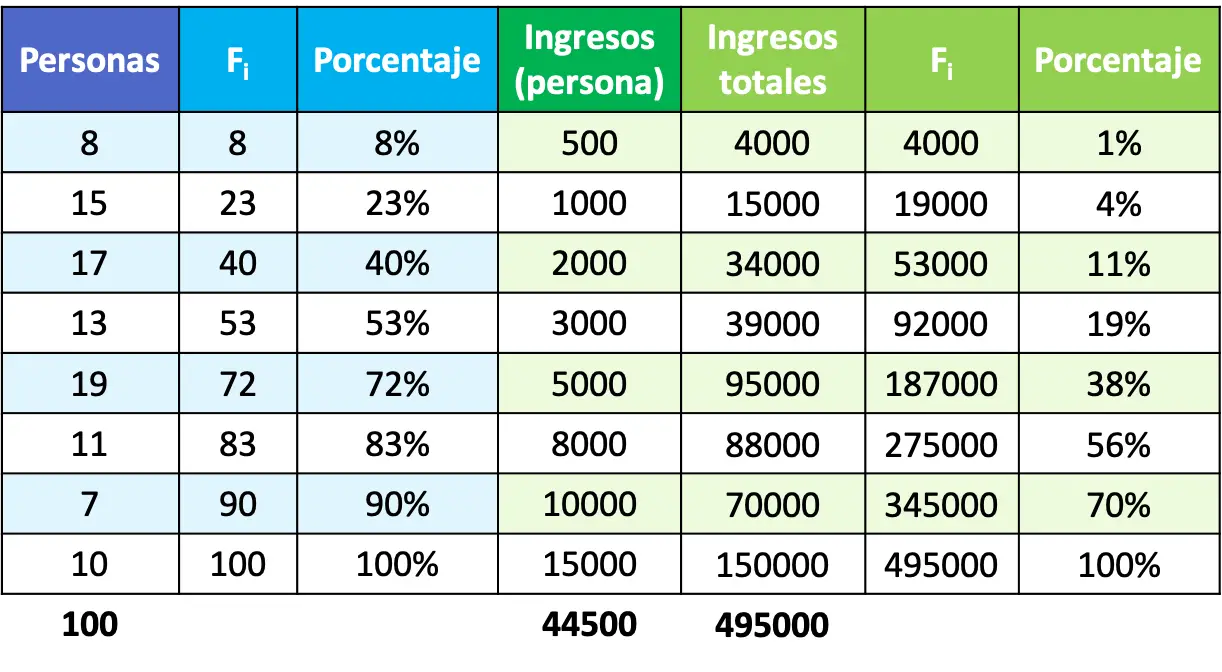
สุดท้ายนี้ หลังจากที่เราได้คำนวณเปอร์เซ็นต์แล้ว เหลือเพียงการพล็อตจุดบนกราฟและนำมารวมกันเพื่อสร้างเส้นโค้งลอเรนซ์ โปรดจำไว้ว่าแกน X คือเปอร์เซ็นต์ของประชากร และแกน Y คือเปอร์เซ็นต์ของรายได้

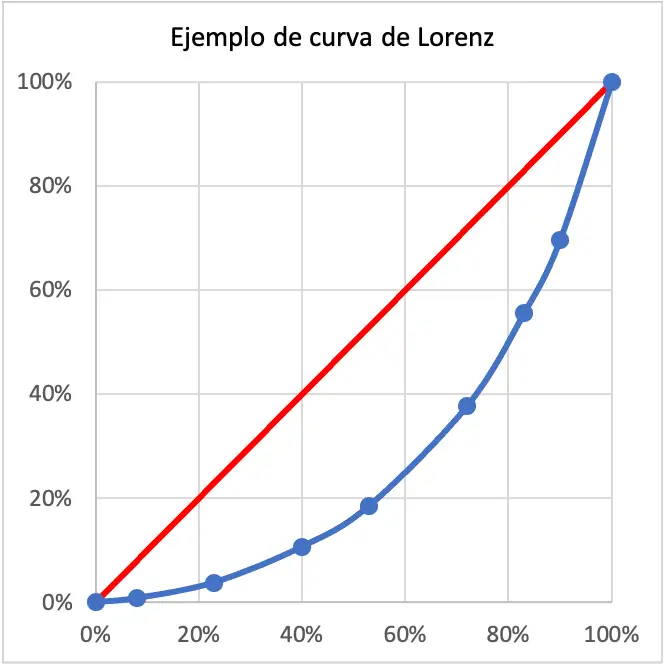
ในกรณีนี้ รายได้ของประชากรที่ศึกษาไม่เท่ากันอย่างมาก เนื่องจากเส้นโค้งลอเรนซ์กว้างมาก ในความเป็นจริง เส้นโค้งลอเรนซ์อยู่ไกลจากเส้นสีแดงซึ่งแสดงถึงความเท่าเทียมกันที่สมบูรณ์แบบ

การตีความเส้นโค้งลอเรนซ์

ในส่วนนี้จะอธิบายวิธีตีความเส้นโค้งลอเรนซ์ของประชากร เนื่องจากนอกจากจะรู้วิธีสร้างกราฟแล้ว คุณยังต้องเข้าใจว่ามันหมายถึงอะไรด้วย

เส้นโค้ง Lorenz ระบุเปอร์เซ็นต์ของประชากรที่เป็นเจ้าของเปอร์เซ็นต์ของรายได้รวมของดินแดน ตัวอย่างเช่น ในตัวอย่างกราฟ Lorenz ที่แสดงด้านบน 40% ของประชากรมีรายได้เท่ากับ 11% ของรายได้ของประชากรทั้งหมด มันจึงเป็นอาณาเขตที่ไม่เรียบมาก

ดังนั้น เส้นโค้งลอเรนซ์จึงแสดงถึงความเท่าเทียมกันหรือความไม่เท่าเทียมกันของรายได้ ระหว่างผู้อยู่อาศัยในประเทศหรือดินแดนหนึ่งๆ ยิ่งเราเคลื่อนห่างจากเส้นที่แสดงถึงความเท่าเทียมกันอย่างสมบูรณ์มากเท่าไร ก็ยิ่งหมายความว่ารายได้ของประชากรไม่เท่าเทียมกันมากขึ้นเท่านั้น ในทางกลับกัน ยิ่งเส้นโค้ง Lorenz ชิดขวามากเท่าไร ก็ยิ่งแสดงว่ารายได้ของประชากรได้รับการกระจายอย่างเท่าเทียมกันมากขึ้นเท่านั้น

นอกจากนี้ หากเส้นโค้งลอเรนซ์เส้นหนึ่งอยู่เหนือเส้นโค้งลอเรนซ์อีกเส้นหนึ่งตลอดทั้งกราฟ นั่นหมายความว่ารายได้ของประชากรกลุ่มแรกมากกว่ารายได้ของประชากรกลุ่มที่สอง

เส้นโค้งลอเรนซ์และสัมประสิทธิ์จินี

ตามที่อธิบายไว้ตลอดทั้งบทความ กราฟ Lorenz แสดงให้เห็นอย่างชัดเจนว่ารายได้ของอาณาเขตมีการกระจายอย่างไร และอาณาเขตมีความไม่เท่ากันเพียงใด

ในทางกลับกัน ค่าสัมประสิทธิ์จินี หรือที่เรียกว่าดัชนีจินี บ่งชี้ถึงความไม่เท่าเทียมกันทางเศรษฐกิจของดินแดนเป็นตัวเลข

เส้นโค้งลอเรนซ์และสัมประสิทธิ์จินีจึงเชื่อมโยงกัน อันที่จริง ค่าสัมประสิทธิ์จินีของประเทศสามารถคำนวณได้จากเส้นโค้งลอเรนซ์ ในบทความต่อไปนี้ คุณสามารถดูวิธีดำเนินการนี้ได้:

คุณสมบัติของเส้นโค้งลอเรนซ์

เส้นโค้ง Lorenz มีคุณสมบัติดังต่อไปนี้:

• เส้น Lorenz เริ่มต้นที่จุด (0,0) และสิ้นสุดที่ (100,100) เสมอ
• ไม่สามารถกำหนดเส้นโค้งลอเรนซ์ได้หากค่าเฉลี่ยตัวอย่างเป็นศูนย์
• เส้นโค้ง Lorenz ไม่สามารถปรากฏบนกราฟเหนือเส้นที่มีความเท่าเทียมกันอย่างสมบูรณ์
• สมมติว่ารายได้ไม่สามารถติดลบได้ เส้น Lorenz จะเพิ่มขึ้นเสมอ