วิธีสร้าง roc curve ใน sas

การถดถอยแบบลอจิสติก เป็นวิธีการที่เราสามารถใช้เพื่อให้พอดีกับแบบจำลองการถดถอยเมื่อตัวแปรตอบสนองเป็นไบนารี

เพื่อประเมินว่าแบบจำลองการถดถอยโลจิสติกเหมาะสมกับชุดข้อมูลได้ดีเพียงใด เราสามารถดูตัวชี้วัดสองตัวต่อไปนี้:

• ความไว: ความน่าจะเป็นที่แบบจำลองคาดการณ์ผลลัพธ์ที่เป็นบวกสำหรับการสังเกต เมื่อผลลัพธ์เป็นบวกจริงๆ สิ่งนี้เรียกอีกอย่างว่า “อัตราบวกที่แท้จริง”
• ความจำเพาะ: ความน่าจะเป็นที่แบบจำลองทำนายผลลัพธ์ที่เป็นลบสำหรับการสังเกต เมื่อผลลัพธ์เป็นลบจริงๆ สิ่งนี้เรียกอีกอย่างว่า “อัตราติดลบที่แท้จริง”

วิธีหนึ่งในการแสดงภาพการวัดทั้งสองนี้คือการสร้าง เส้นโค้ง ROC ซึ่งย่อมาจากเส้นโค้ง “ลักษณะการทำงานของตัวรับ” นี่คือกราฟที่แสดงความไวและความเฉพาะเจาะจงของแบบจำลองการถดถอยลอจิสติก

ตัวอย่างทีละขั้นตอนต่อไปนี้แสดงวิธีสร้างและตีความเส้นโค้ง ROC ใน SAS

ขั้นตอนที่ 1: สร้างชุดข้อมูล

ขั้นแรก เราจะสร้างชุดข้อมูลที่ประกอบด้วยข้อมูลเกี่ยวกับตัวแปรต่อไปนี้สำหรับนักเรียน 18 คน:

• การรับเข้าเรียนในวิทยาลัยบางแห่ง (1 = ใช่, 0 = ไม่ใช่)
• เกรดเฉลี่ย (ระดับ 1 ถึง 4)
• คะแนน ACT (ระดับ 1 ถึง 36)

 /*create dataset*/
data my_data;
    input acceptance gpa act;
    datalines ;
1 3 30
0 1 21
0 2 26
0 1 24
1 3 29
1 3 34
0 3 31
1 2 29
0 1 21
1 2 21
0 1 15
1 3 32
1 4 31
1 4 29
0 1 24
1 4 29
1 3 21
1 4 34
;
run ;

ขั้นตอนที่ 2: ปรับโมเดลการถดถอยโลจิสติกและสร้างเส้นโค้ง ROC

ต่อไป เราจะใช้ proc Logistics เพื่อให้เหมาะสมกับโมเดลการถดถอยโลจิสติก โดยใช้ “การยอมรับ” เป็นตัวแปรตอบสนอง และใช้ “gpa” และ “act” เป็นตัวแปรทำนาย

เราจะระบุ การลดลง เพื่อให้ SAS รู้วิธีทำนายความน่าจะเป็นที่ตัวแปรตอบสนองจะใช้ค่า 1

นอกจากนี้เรายังจะใช้ plots(only)=roc เพื่อสร้างเส้นโค้ง ROC สำหรับโมเดล:

 /*fit logistic regression model & create ROC curve*/
proc logistic data =my_data descending plots ( only )=roc;
  model acceptance = gpa act;
run ;

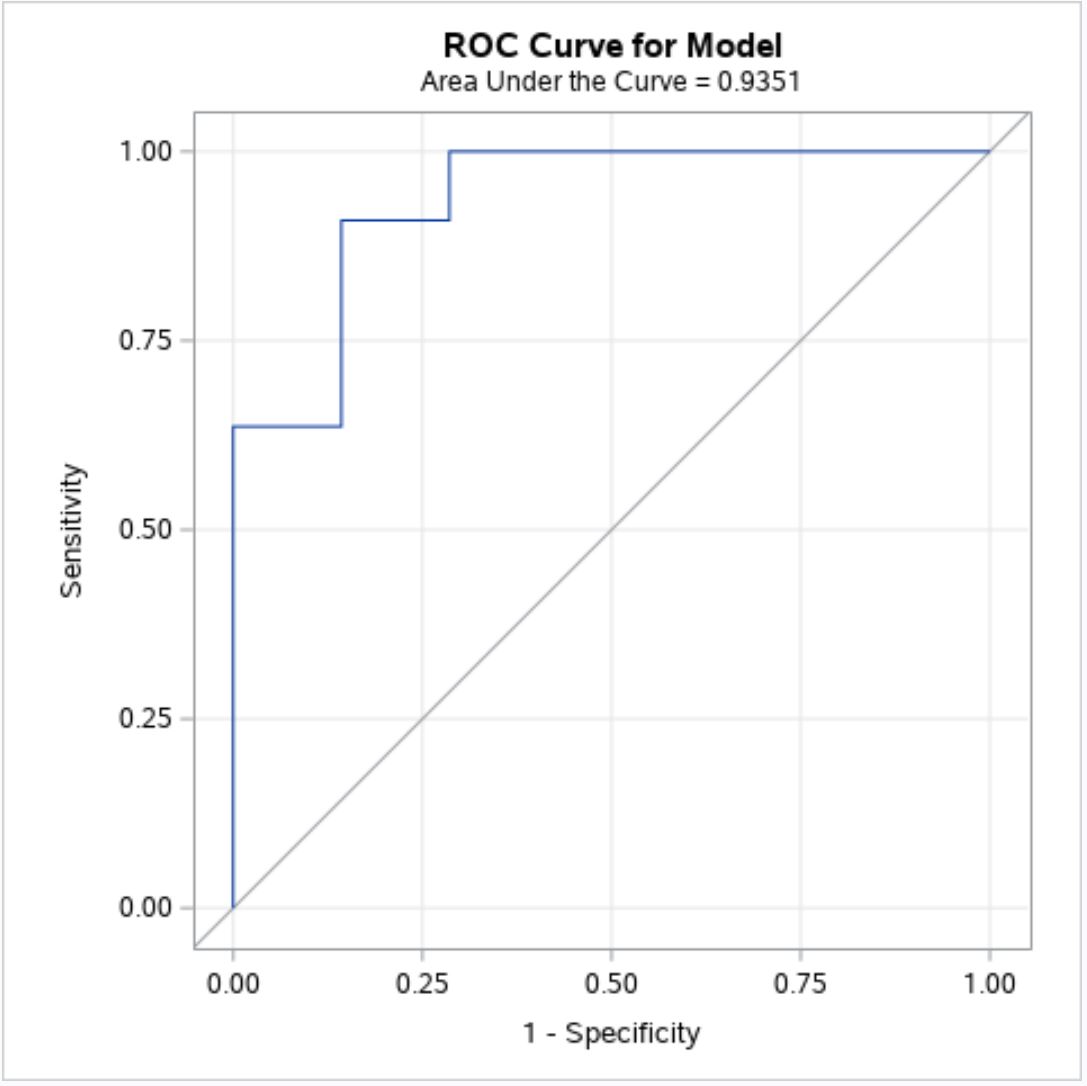
ขั้นตอนที่ 3: ตีความเส้นโค้ง ROC

ยิ่งเส้นโค้ง ROC พอดีกับมุมซ้ายบนของโครงเรื่องมากเท่าใด โมเดลก็จะคาดการณ์ค่าของค่าตอบสนองในชุดข้อมูลได้ดีขึ้นเท่านั้น

จากกราฟด้านบน เราจะเห็นว่าเส้นโค้ง ROC สีน้ำเงินมีแนวโน้มที่จะโอบมุมซ้ายบน ซึ่งบ่งชี้ว่าแบบจำลองการถดถอยโลจิสติกทำงานได้ดีในการทำนายค่าของค่าตอบสนอง

ในการหาปริมาณว่าแบบจำลองการถดถอยโลจิสติกเหมาะสมกับข้อมูลมากน้อยเพียงใด เราสามารถคำนวณ AUC ซึ่งเป็นพื้นที่ใต้เส้นโค้ง ซึ่งจะบอกเราว่าโครงเรื่องอยู่ใต้เส้นโค้งเป็นจำนวนเท่าใด

ยิ่ง AUC ใกล้ 1 มากเท่าใด โมเดลก็ยิ่งดีเท่านั้น โมเดลที่มี AUC เท่ากับ 0.5 ไม่ได้ดีไปกว่าโมเดลที่มีการจำแนกแบบสุ่ม

ใต้ชื่อกราฟด้านบน เราจะเห็นว่า AUC ของรุ่นนี้คือ 0.9351

เนื่องจากค่านี้อยู่ใกล้หนึ่งจึงเป็นการยืนยันว่าโมเดลทำนายค่าของค่าตอบสนองได้ดี

นอกจากนี้เรายังสามารถใช้ค่า AUC เพื่อเปรียบเทียบความเหมาะสมของแบบจำลองการถดถอยโลจิสติกต่างๆ

ตัวอย่างเช่น สมมติว่าเราใส่โมเดลการถดถอยโลจิสติกที่แตกต่างกันสองแบบ และคำนวณค่า AUC สำหรับแต่ละโมเดล:

• AUC ของโมเดล 1: 0.9351
• AUC ของโมเดล 2: 0.8140

เนื่องจาก AUC ของโมเดล 1 มีขนาดใหญ่ จึงบอกเราว่าโมเดล 1 ทำงานได้ดีกว่าในการปรับข้อมูลให้เหมาะสมกว่าโมเดล 2

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้จะอธิบายวิธีดำเนินการทั่วไปอื่นๆ ใน SAS:

วิธีดำเนินการถดถอยเชิงเส้นอย่างง่ายใน SAS
วิธีดำเนินการถดถอยเชิงเส้นพหุคูณใน SAS
วิธีดำเนินการถดถอยโลจิสติกใน SAS