วิธีใช้ตาราง z (พร้อมตัวอย่าง)
ตาราง az คือตารางที่บอกคุณว่าเปอร์เซ็นต์ของค่าที่อยู่ต่ำกว่าคะแนน z ที่กำหนดในการแจกแจงแบบปกติมาตรฐาน
คะแนน z เพียงบอกคุณว่าค่าข้อมูลแต่ละรายการตกไปจากค่าเฉลี่ยเป็นจำนวนเท่าใด มีการคำนวณดังนี้:
คะแนน z = (x – μ) / σ
ทอง:
- x: ค่าข้อมูลแต่ละรายการ
- μ: ค่าเฉลี่ยประชากร
- σ: ส่วนเบี่ยงเบนมาตรฐานประชากร
บทช่วยสอนนี้แสดงตัวอย่างต่างๆ ของการใช้ตาราง z
ตัวอย่างที่ 1
โดยทั่วไปคะแนนในการสอบเข้าวิทยาลัยบางแห่งจะแจกแจงโดยมีค่าเฉลี่ย μ = 82 และส่วนเบี่ยงเบนมาตรฐาน σ = 8 นักเรียนมีคะแนนต่ำกว่า 84 ในการสอบประมาณกี่เปอร์เซ็นต์
ขั้นตอนที่ 1: ค้นหาคะแนน z
อันดับแรก เราจะหาคะแนน z ที่เกี่ยวข้องกับคะแนนสอบ 84:
คะแนน z = (x – μ) / σ = (84 – 82) / 8 = 2/8 = 0.25
ขั้นตอนที่ 2: ใช้แผนภูมิ z เพื่อค้นหาเปอร์เซ็นต์ที่สอดคล้องกับคะแนน z
ต่อไปเราจะค้นหาค่า 0.25 ในตาราง z:

นักเรียนประมาณ 59.87% มีคะแนนต่ำกว่า 84 ในการสอบนี้
ตัวอย่างที่ 2
ความสูงของต้นไม้ในสวนบางแห่งโดยปกติจะกระจายโดยมีค่าเฉลี่ย μ = 26.5 นิ้ว และค่าเบี่ยงเบนมาตรฐาน σ = 2.5 นิ้ว ต้นไม้สูงเกิน 26 นิ้วมีประมาณกี่เปอร์เซ็นต์?
ขั้นตอนที่ 1: ค้นหาคะแนน z
อันดับแรก เราจะหาคะแนน z ที่เกี่ยวข้องกับส่วนสูง 26 นิ้ว
คะแนน z = (x – μ) / σ = (26 – 26.5) / 2.5 = -0.5 / 2.5 = -0.2
ขั้นตอนที่ 2: ใช้แผนภูมิ z เพื่อค้นหาเปอร์เซ็นต์ที่สอดคล้องกับคะแนน z
ต่อไปเราจะค้นหาค่า -0.2 ในตาราง z:
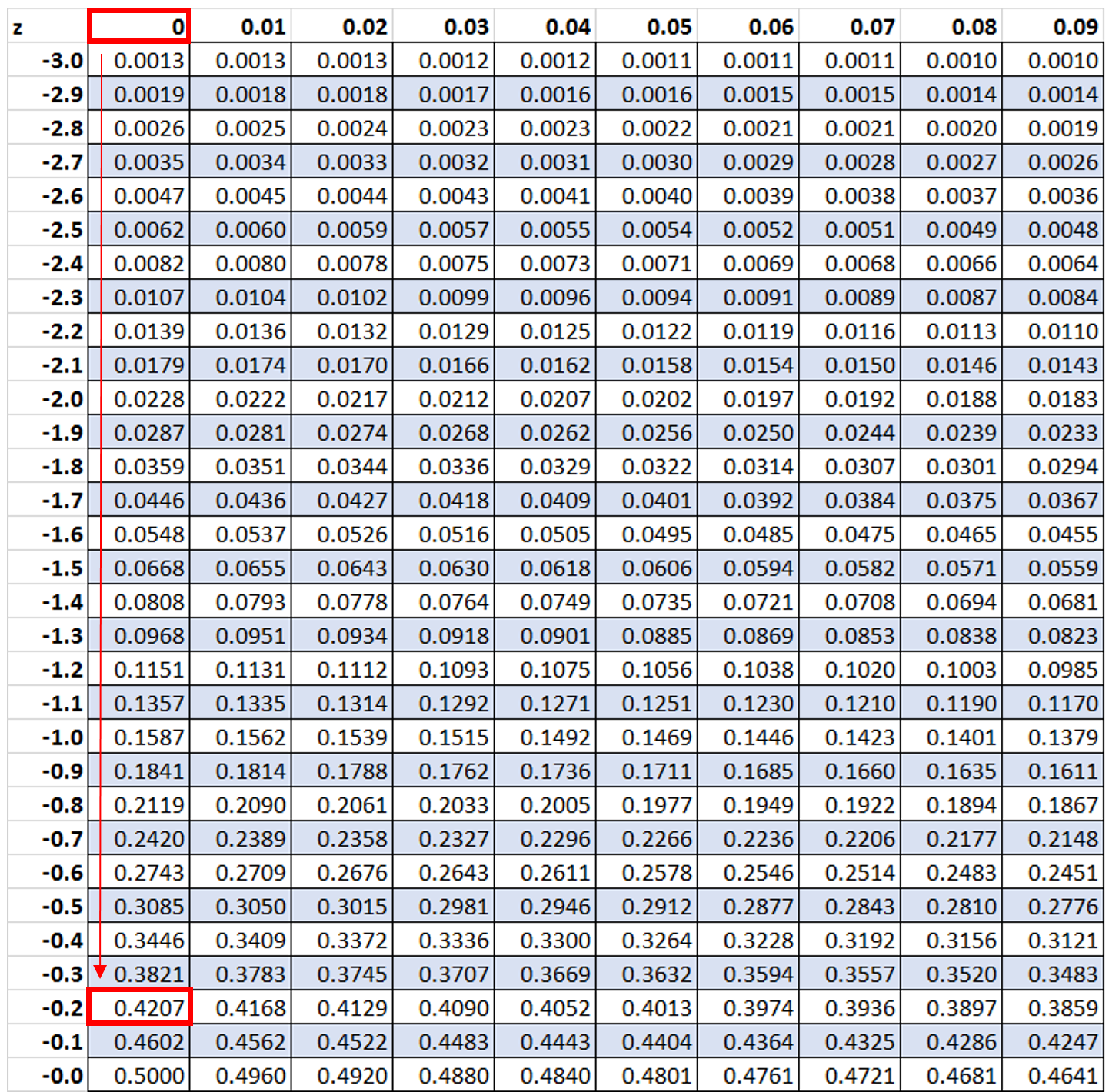
เราพบว่า 42.07% ของค่าอยู่ต่ำกว่าคะแนน z ที่ -0.2 อย่างไรก็ตาม ในตัวอย่างนี้ เราต้องการทราบว่าค่าที่ มากกว่า -0.2 เปอร์เซ็นต์เป็นเท่าใด ซึ่งเราสามารถหาได้จากสูตร 100% – 42.07% = 57.93%
ดังนั้นประมาณ 59.87% ของพืชในสวนแห่งนี้จึงสูงเกิน 26 นิ้ว
ตัวอย่างที่ 3
โดยปกติน้ำหนักของโลมาบางชนิดจะกระจายโดยมีค่าเฉลี่ย μ = 400 ปอนด์ และค่าเบี่ยงเบนมาตรฐานที่ σ = 25 ปอนด์ โลมามีน้ำหนักระหว่าง 410 ถึง 425 ปอนด์ประมาณกี่เปอร์เซ็นต์
ขั้นตอนที่ 1: ค้นหาคะแนน z
ขั้นแรก เราจะค้นหาคะแนน z ที่เกี่ยวข้องกับหนังสือ 410 เล่มและหนังสือ 425 เล่ม
คะแนน z ของ 410 = (x – μ) / σ = (410 – 400) / 25 = 10/25 = 0.4
คะแนน z ของ 425 = (x – μ) / σ = (425 – 400) / 25 = 25 / 25 = 1
ขั้นตอนที่ 2: ใช้แผนภูมิ z เพื่อค้นหาเปอร์เซ็นต์ที่สอดคล้องกับคะแนน z แต่ละรายการ
ก่อนอื่น เราจะหาค่า 0.4 ในตาราง z:

ต่อไปเราจะหาค่า 1 ในตาราง z:

สุดท้าย เราจะลบค่าที่น้อยที่สุดออกจากค่าที่ใหญ่ที่สุด: 0.8413 – 0.6554 = 0.1859
ดังนั้นโลมาประมาณ 18.59% มีน้ำหนักระหว่าง 410 ถึง 425 ปอนด์
แหล่งข้อมูลเพิ่มเติม
ความรู้เบื้องต้นเกี่ยวกับการแจกแจงแบบปกติ
เครื่องคำนวณพื้นที่การแจกแจงแบบปกติ
เครื่องคิดเลขคะแนน Z