สถิติการทดสอบมาตรฐานคืออะไร?

สมมติฐานทางสถิติ คือ สมมติฐานเกี่ยวกับ พารามิเตอร์ประชากร ตัวอย่างเช่น เราสามารถสรุปได้ว่าความสูงเฉลี่ยของผู้ชายในสหรัฐอเมริกาคือ 70 นิ้ว สมมติฐานเกี่ยวกับความสูงเป็น สมมติฐานทางสถิติ และความสูงเฉลี่ยที่แท้จริงของผู้ชายในสหรัฐอเมริกาคือ พารามิเตอร์ประชากร

การทดสอบสมมติฐาน คือการทดสอบทางสถิติอย่างเป็นทางการที่เราใช้เพื่อปฏิเสธหรือไม่ปฏิเสธสมมติฐานทางสถิติ

กระบวนการพื้นฐานในการดำเนินการทดสอบสมมติฐานมีดังนี้

1. รวบรวมข้อมูลตัวอย่าง

2. คำนวณสถิติการทดสอบมาตรฐานสำหรับข้อมูลตัวอย่าง

3. เปรียบเทียบสถิติการทดสอบมาตรฐานกับค่าวิกฤต ถ้ามันสุดขั้วมากกว่าค่าวิกฤติ ให้ปฏิเสธสมมติฐานว่าง มิฉะนั้น อย่าปฏิเสธการทดสอบสมมติฐานว่าง

สูตรที่เราใช้ในการคำนวณ สถิติการทดสอบที่เป็นมาตรฐาน จะแตกต่างกันไปขึ้นอยู่กับประเภทของการทดสอบสมมติฐานที่เรากำลังดำเนินการ

ตารางต่อไปนี้แสดงสูตรที่จะใช้คำนวณสถิติการทดสอบมาตรฐานสำหรับการทดสอบสมมติฐานหลักแต่ละประเภทจากสี่ประเภท:

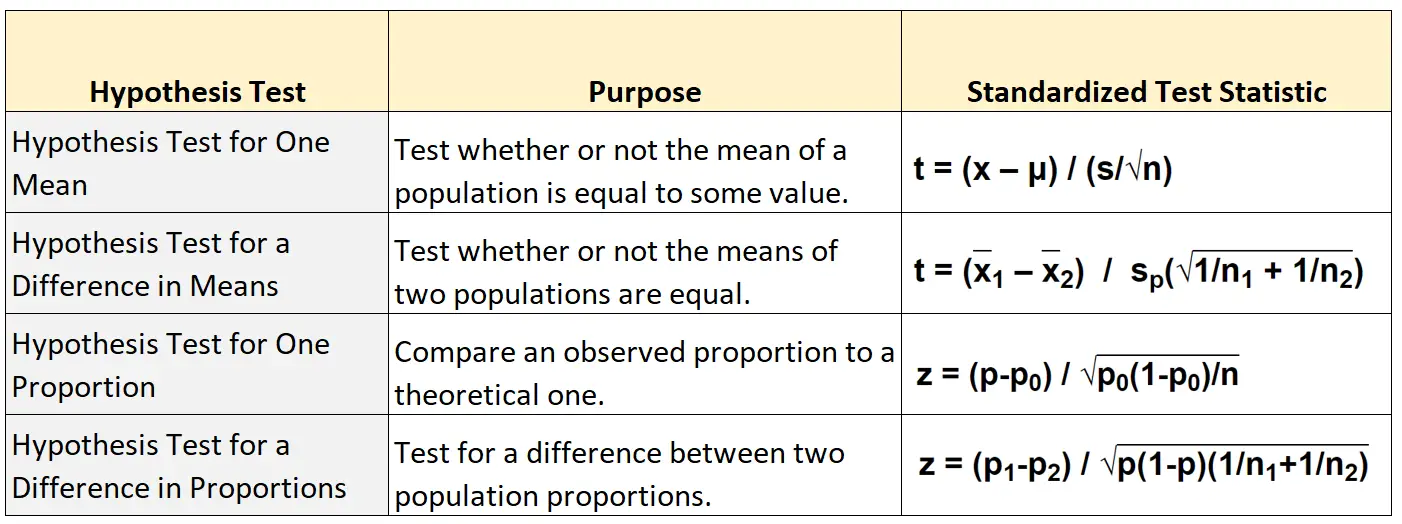
การทดสอบสมมุติฐานโดยเฉลี่ย

การทดสอบทีแบบตัวอย่างเดียว ใช้เพื่อทดสอบว่าค่าเฉลี่ยของประชากรเท่ากับค่าที่กำหนดหรือไม่

สถิติการทดสอบมาตรฐานสำหรับการทดสอบประเภทนี้มีการคำนวณดังนี้:

เสื้อ = ( X – μ) / (s/√n)

ทอง:

• x: ค่าเฉลี่ยตัวอย่าง
• μ ₀ : ค่าเฉลี่ยประชากรสมมุติ
• s: ค่าเบี่ยงเบนมาตรฐานตัวอย่าง
• n: ขนาดตัวอย่าง

ดู บทช่วยสอนนี้ เพื่อดูตัวอย่างการคำนวณสถิติการทดสอบมาตรฐานนี้

การทดสอบสมมติฐานเพื่อหาความแตกต่างในค่าเฉลี่ย

การทดสอบทีแบบสองตัวอย่าง ใช้เพื่อทดสอบว่าค่าเฉลี่ยของประชากรทั้งสองเท่ากันหรือไม่

สถิติการทดสอบมาตรฐานสำหรับการทดสอบประเภทนี้มีการคำนวณดังนี้:

เสื้อ = ( X ₁ – X ₂ ) / _sp (√ 1/n ₁ + 1/n ₂ )

โดยที่ x ₁ และ x ₂ เป็นค่าเฉลี่ยตัวอย่าง n ₁ และ n ₂ คือขนาดตัวอย่าง และโดยที่ s _p คำนวณได้ดังนี้

_sp = √ (n ₁ -1)s ₁ ² + (n ₂ -1)s ₂ ² / (n ₁ +n ₂ -2)

โดยที่ s ₁ ² และ s ₂ ² คือความแปรปรวนตัวอย่าง

ดู บทช่วยสอนนี้ เพื่อดูตัวอย่างการคำนวณสถิติการทดสอบมาตรฐานนี้

การทดสอบสมมติฐานสำหรับสัดส่วน

การทดสอบค่า z แบบสัดส่วนเดียว ใช้เพื่อเปรียบเทียบสัดส่วนที่สังเกตได้กับสัดส่วนทางทฤษฎี

สถิติการทดสอบมาตรฐานสำหรับการทดสอบประเภทนี้มีการคำนวณดังนี้:

z = (หน้า ₀ ) / √ p ₀ (1-p ₀ )/n

ทอง:

• p: สัดส่วนตัวอย่างที่สังเกตได้
• p ₀ : สัดส่วนสมมุติฐานของประชากร
• n: ขนาดตัวอย่าง

ดู บทช่วยสอนนี้ เพื่อดูตัวอย่างการคำนวณสถิติการทดสอบมาตรฐานนี้

การทดสอบสมมติฐานเพื่อหาความแตกต่างในสัดส่วน

การทดสอบค่า z แบบสองสัดส่วน ใช้เพื่อทดสอบความแตกต่างระหว่างสัดส่วนประชากรสองสัดส่วน

สถิติการทดสอบมาตรฐานสำหรับการทดสอบประเภทนี้มีการคำนวณดังนี้:

z = (p ₁ -p ₂ ) / √ p(1-p)(1/n ₁ +1/n ₂ )

โดยที่ p ₁ และ p ₂ คือสัดส่วนตัวอย่าง n ₁ และ n ₂ คือขนาดตัวอย่าง และโดยที่ p คือสัดส่วนรวมรวมที่คำนวณได้ดังนี้:

พี = (พี ₁ n ₁ + พี ₂ n ₂ )/( n ₁ + n ₂ )

ดู บทช่วยสอนนี้ เพื่อดูตัวอย่างการคำนวณสถิติการทดสอบมาตรฐานนี้