วิธีทดสอบความเป็นปกติใน stata

การทดสอบทางสถิติจำนวนมากกำหนดให้มี การกระจายตัวแปรตั้งแต่หนึ่งตัวขึ้นไปตามปกติ เพื่อให้ผลการทดสอบเชื่อถือได้

บทช่วยสอนนี้จะอธิบายวิธีการต่างๆ ที่คุณสามารถใช้เพื่อทดสอบความเป็นปกติระหว่างตัวแปรใน Stata

สำหรับแต่ละวิธีเหล่านี้ เราจะใช้ชุดข้อมูล Stata ในตัวที่เรียกว่า auto คุณสามารถโหลดชุดข้อมูลนี้โดยใช้คำสั่งต่อไปนี้:

การใช้งานระบบอัตโนมัติ

วิธีที่ 1: ฮิสโตแกรม

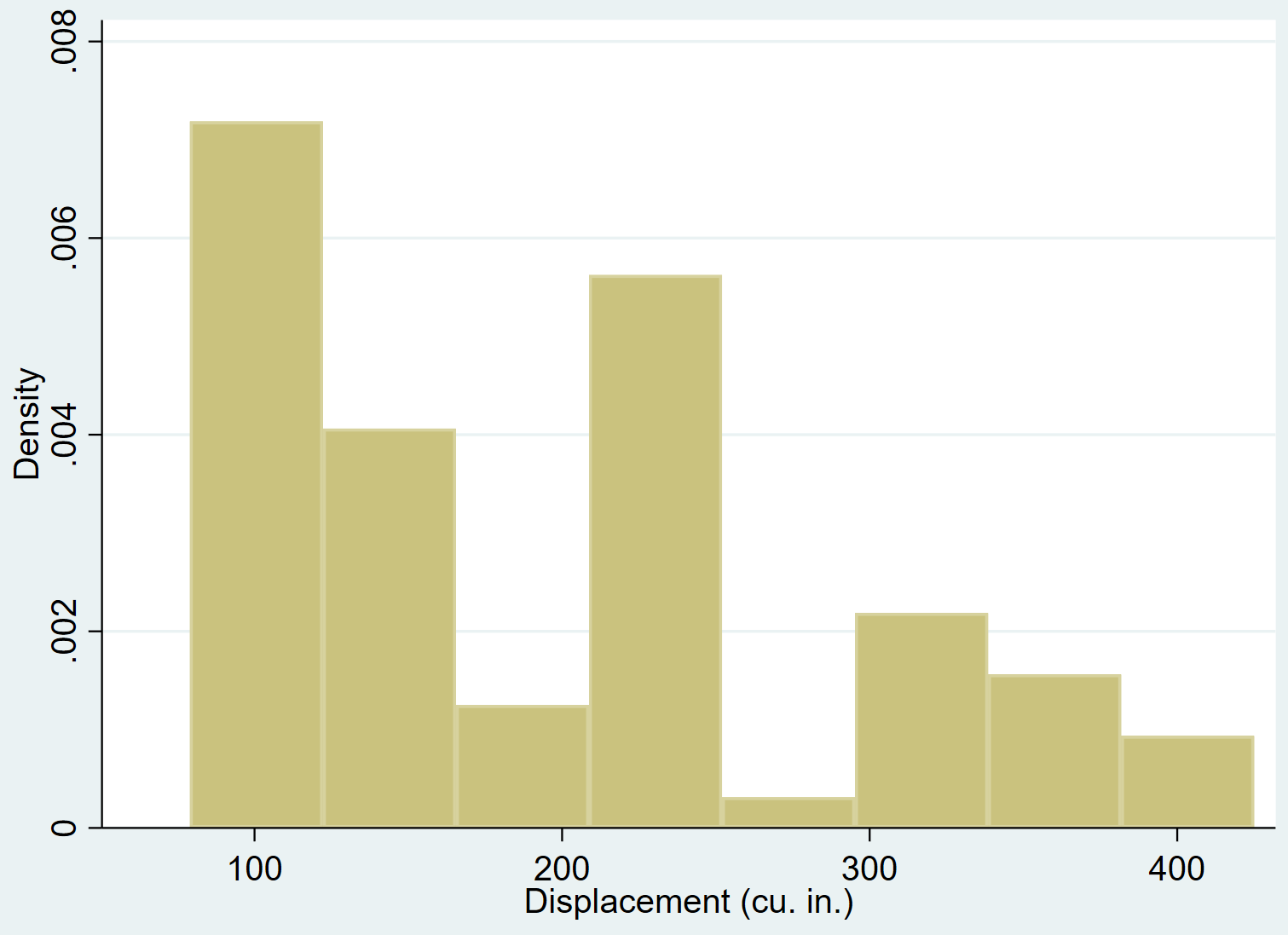
วิธีที่ไม่เป็นทางการเพื่อดูว่าตัวแปรมีการกระจายตามปกติหรือไม่คือการสร้าง ฮิสโตแกรม เพื่อแสดงการกระจายของตัวแปร

หาก มี การกระจายตัวแปรตามปกติ ฮิสโตแกรมควรอยู่ในรูป “ระฆัง” โดยมีค่ามากกว่าตรงกลางและค่าน้อยกว่าอยู่ที่ส่วนท้าย

เราสามารถใช้คำสั่ง hist เพื่อสร้างฮิสโตแกรมสำหรับ การกระจัด ของตัวแปร :

ประวัติศาสตร์ที่เคลื่อนไหว

เราสามารถเพิ่ม เส้นโค้งความหนาแน่น ปกติให้กับฮิสโตแกรมได้โดยใช้คำสั่ง ปกติ :

ย้ายประวัติปกติ

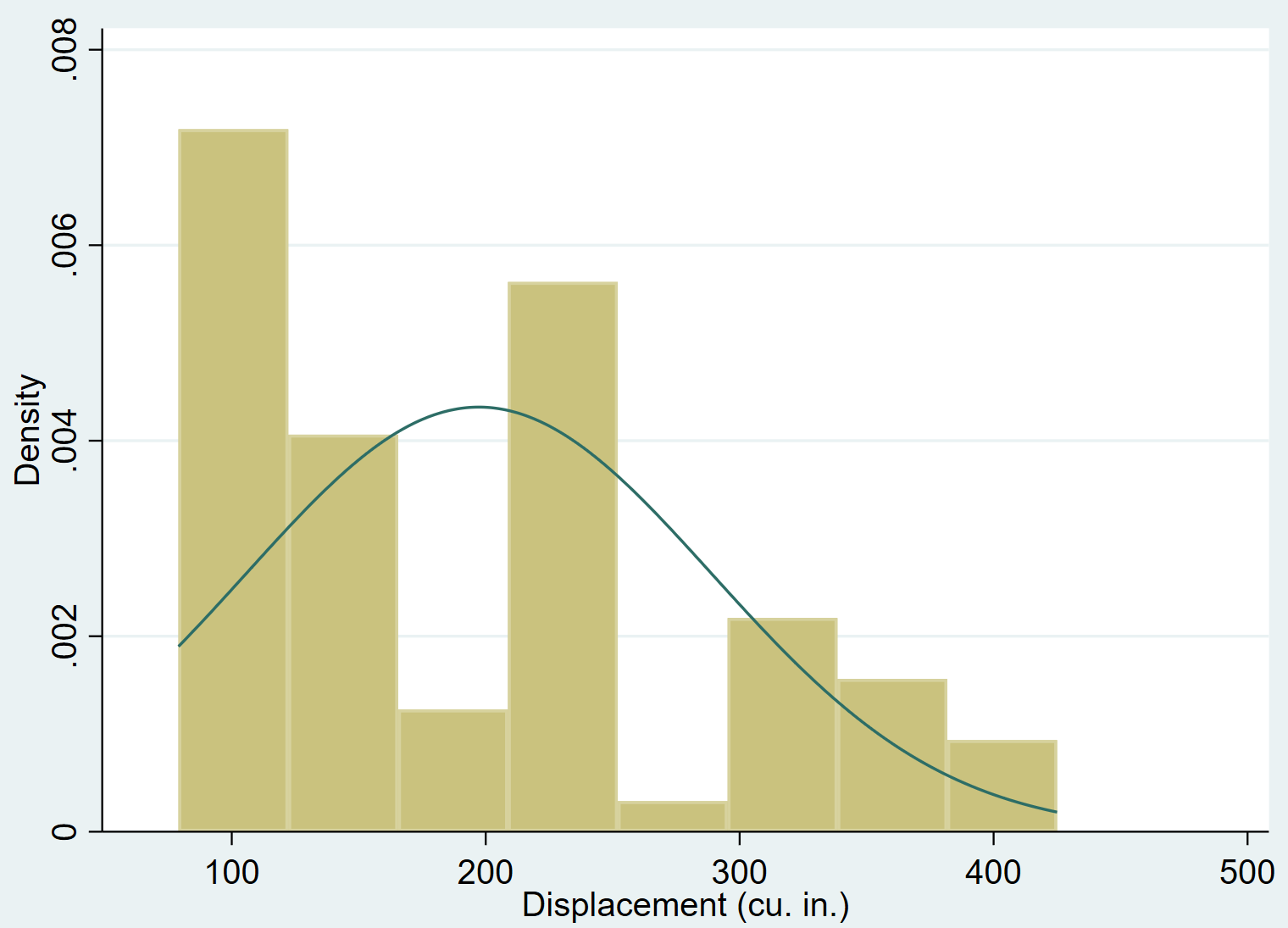
เห็นได้ชัดว่าการเปลี่ยนแปลงของ ตัวแปรเอียง ไปทางขวา (เช่น ค่าส่วนใหญ่จะเน้นไปทางซ้าย และค่า “หาง” ยาวจะขยายไปทางขวา) และไม่เป็นไปตามการแจกแจงแบบปกติ

ที่เกี่ยวข้อง: การแจกแจงแบบเบ้ซ้ายและขวา

วิธีที่ 2: การทดสอบชาปิโร-วิลค์

วิธีทดสอบความเป็นปกติอย่างเป็นทางการคือการใช้ การทดสอบชาปิโร-วิลค์

สมมติฐานว่างสำหรับการทดสอบนี้คือตัวแปรมีการกระจายตามปกติ หาก ค่า p ของการทดสอบต่ำกว่าระดับนัยสำคัญที่กำหนด (ตัวเลือกทั่วไป ได้แก่ 0.01, 0.05 และ 0.10) เราก็สามารถปฏิเสธสมมติฐานว่างและสรุปว่ามีหลักฐานเพียงพอที่จะยืนยันว่าตัวแปรนั้นไม่มีการกระจายตามปกติ .

*การทดสอบนี้สามารถใช้ได้เมื่อจำนวนการสังเกตทั้งหมดอยู่ระหว่าง 4 ถึง 2,000 ครั้ง

เราสามารถใช้คำสั่ง swilk เพื่อทำการทดสอบ Shapiro-Wilk เกี่ยวกับ การกระจัด ของตัวแปร :

การเคลื่อนไหวที่ราบรื่น

ต่อไปนี้เป็นวิธีการตีความผลการทดสอบ:

Obs: 74 นี่คือจำนวนข้อสังเกตที่ใช้ในการทดสอบ

ว: 0.92542. นี่คือสถิติการทดสอบสำหรับการทดสอบ

ปัญหา>z: 0.00031 นี่คือค่า p ที่เกี่ยวข้องกับสถิติการทดสอบ

เนื่องจากค่า p น้อยกว่า 0.05 เราจึงสามารถปฏิเสธสมมติฐานว่างของการทดสอบได้ เรามีหลักฐานเพียงพอที่จะบอกว่า การกระจัดของ ตัวแปรนั้นไม่มีการกระจายตามปกติ

นอกจากนี้เรายังสามารถทำการทดสอบ Shapiro-Wilk กับตัวแปรหลายตัวพร้อมกันได้โดยการแสดงรายการตัวแปรหลายตัวหลังคำสั่ง swilk :

ความยาว mpg แทนที่ swilk

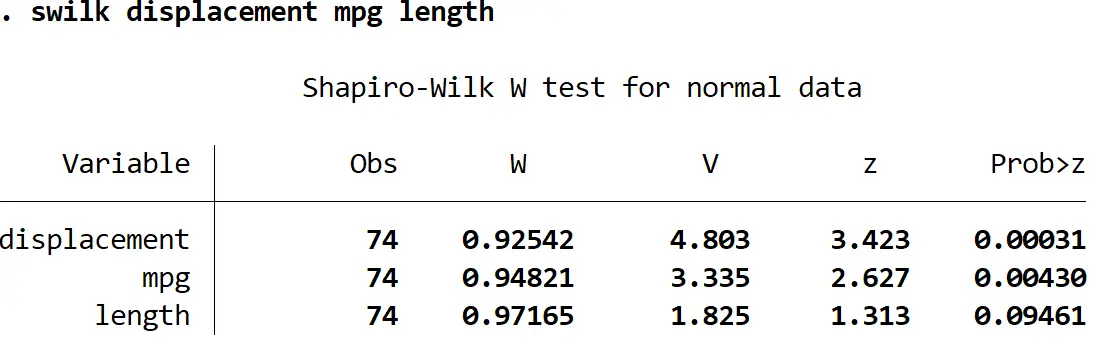
เมื่อใช้ระดับนัยสำคัญที่ 0.05 เราจะสรุปได้ว่า การกระจัด และ MPG ไม่ได้กระจายตามปกติ แต่เราไม่มีหลักฐานเพียงพอที่จะบอกว่าความ ยาว ไม่ได้กระจายตามปกติ

วิธีที่ 3: การทดสอบชาปิโร-ฟรานเซีย

อีกวิธีอย่างเป็นทางการในการทดสอบความเป็นปกติคือใช้ การทดสอบชาปิโร-ฟรานเซีย

สมมติฐานว่างสำหรับการทดสอบนี้คือตัวแปรมีการกระจายตามปกติ หากค่า p ของการทดสอบต่ำกว่าระดับนัยสำคัญที่กำหนด เราก็สามารถปฏิเสธสมมติฐานว่างและสรุปได้ว่ามีหลักฐานเพียงพอที่จะบอกว่าตัวแปรนั้นไม่ได้มีการแจกแจงแบบปกติ

*การทดสอบนี้สามารถใช้ได้เมื่อจำนวนการสังเกตทั้งหมดอยู่ระหว่าง 10 ถึง 5,000 ครั้ง

เราสามารถใช้คำสั่ง sfrancia เพื่อทำการทดสอบ Shapiro-Wilk กับ การกระจัด ของตัวแปร :

ย้ายสฟรานเซีย

ต่อไปนี้เป็นวิธีการตีความผลการทดสอบ:

Obs: 74 นี่คือจำนวนข้อสังเกตที่ใช้ในการทดสอบ

W’: 0.93011. นี่คือสถิติการทดสอบสำหรับการทดสอบ

ปัญหา>z: 0.00094 นี่คือค่า p ที่เกี่ยวข้องกับสถิติการทดสอบ

เนื่องจากค่า p น้อยกว่า 0.05 เราจึงสามารถปฏิเสธสมมติฐานว่างของการทดสอบได้ เรามีหลักฐานเพียงพอที่จะบอกว่า การกระจัดของ ตัวแปรนั้นไม่มีการกระจายตามปกติ

เช่นเดียวกับการทดสอบ Shapiro-Wilk คุณสามารถทำการทดสอบ Shapiro-Francia กับตัวแปรหลายตัวพร้อมกันได้โดยการแสดงรายการตัวแปรหลายตัวหลังคำสั่ง sfrancia

วิธีที่ 4: การทดสอบความเบ้และความโด่ง

อีกวิธีหนึ่งในการทดสอบความเป็นปกติคือการใช้ การทดสอบความเบ้และความโด่ง ซึ่งจะกำหนดว่าความเบ้และความโด่งของตัวแปรนั้นสอดคล้องกับการแจกแจงแบบปกติหรือไม่

สมมติฐานว่างสำหรับการทดสอบนี้คือตัวแปรมีการกระจายตามปกติ หากค่า p ของการทดสอบต่ำกว่าระดับนัยสำคัญที่กำหนด เราก็สามารถปฏิเสธสมมติฐานว่างและสรุปได้ว่ามีหลักฐานเพียงพอที่จะบอกว่าตัวแปรนั้นไม่ได้มีการแจกแจงแบบปกติ

*การทดสอบนี้ต้องใช้การสังเกตอย่างน้อย 8 ครั้ง

เราสามารถใช้คำสั่ง sktest เพื่อทำการทดสอบความเบ้และความโด่งกับ การกระจัด ของตัวแปร :

ย้ายการทดสอบ

ต่อไปนี้เป็นวิธีการตีความผลการทดสอบ:

Obs: 74 นี่คือจำนวนข้อสังเกตที่ใช้ในการทดสอบ

คำวิเศษณ์ไค(2): 5.81 นี่คือสถิติการทดสอบไคสแควร์สำหรับการทดสอบ

Prob>chi2: 0.0547 นี่คือค่า p ที่เกี่ยวข้องกับสถิติการทดสอบ

เนื่องจากค่า p ไม่น้อยกว่า 0.05 เราจึงไม่สามารถปฏิเสธสมมติฐานว่างของการทดสอบได้ เราไม่มีหลักฐานเพียงพอที่จะบอกว่า การเคลื่อนไหว ไม่กระจายตามปกติ

เช่นเดียวกับการทดสอบภาวะปกติอื่นๆ คุณสามารถทำการทดสอบความเบ้และความโด่งกับตัวแปรหลายตัวพร้อมกันได้โดยการแสดงรายการตัวแปรหลายตัวหลังคำสั่ง sktest