คู่มือฉบับสมบูรณ์: วิธีตรวจสอบสมมติฐาน manova

MANOVA (การวิเคราะห์ความแปรปรวนหลายตัวแปร) ใช้เพื่อวิเคราะห์ว่าตัวแปรปัจจัยตั้งแต่หนึ่งตัวขึ้นไปส่งผลต่อตัวแปรตอบสนองหลายตัวอย่างไร

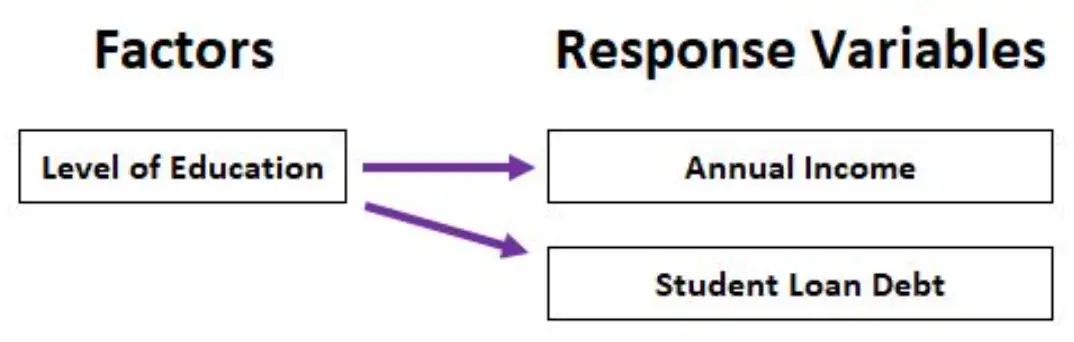
ตัวอย่างเช่น เราสามารถใช้ MANOVA เพื่อวิเคราะห์ว่าระดับการศึกษา (อนุปริญญามัธยมศึกษาตอนปลาย อนุปริญญา ปริญญาตรี ปริญญาโท) ส่งผลต่อรายได้ต่อปีและหนี้เงินกู้นักเรียนทั้งหมดอย่างไร

ที่เกี่ยวข้อง: ความแตกต่างระหว่าง ANOVA, ANCOVA, MANOVA และ MANCOVA

ทุกครั้งที่เราทำ MANOVA เราต้องตรวจสอบว่าเป็นไปตามสมมติฐานต่อไปนี้:

1. ภาวะปกติหลายตัวแปร – ตัวแปรตอบสนองจะกระจายตามปกติหลายตัวแปรภายในแต่ละกลุ่มของตัวแปรปัจจัย

2. ความเป็นอิสระ – การสังเกตแต่ละครั้งจะถูกสุ่มตัวอย่างและสุ่มตัวอย่างอย่างอิสระจากประชากร

3. ความแปรปรวนเท่ากัน – เมทริกซ์ความแปรปรวนร่วมของประชากรแต่ละกลุ่มเท่ากัน

4. ไม่มีค่าผิดปกติหลายตัวแปร – ไม่มีค่าผิดปกติหลายตัวแปรที่รุนแรง

ในบทความนี้ เราจะให้คำอธิบายของแต่ละสมมติฐาน รวมถึงวิธีพิจารณาว่าเป็นไปตามสมมติฐานหรือไม่

สมมติฐานที่ 1: ภาวะปกติหลายตัวแปร

MANOVA ถือว่าตัวแปรตอบสนองมีการกระจายหลายตัวแปรตามปกติภายในแต่ละกลุ่มของตัวแปรตัวประกอบ

หากมีการสังเกตอย่างน้อย 20 รายการสำหรับแต่ละปัจจัย * การรวมกันของตัวแปรตอบสนอง เราสามารถสรุปได้ว่าเป็นไปตามสมมติฐานของภาวะปกติหลายตัวแปร

หากมีการสังเกตน้อยกว่า 20 ครั้งสำหรับแต่ละปัจจัย*การตอบสนอง ตัวแปรผสม เราสามารถสร้างเมทริกซ์ Scatterplot เพื่อแสดงภาพส่วนที่เหลือและตรวจสอบด้วยสายตาว่าเป็นไปตามสมมติฐานนี้หรือไม่

โชคดีที่เป็นที่ทราบกันดีว่า MANOVA สามารถทนต่อการเบี่ยงเบนจากภาวะปกติหลายตัวแปรได้ ดังนั้นการเบี่ยงเบนเล็กน้อยถึงปานกลางโดยทั่วไปจึงไม่เป็นปัญหา

สมมติฐานที่ 2: ความเป็นอิสระ

MANOVA ถือว่าการสังเกตแต่ละครั้งสุ่มตัวอย่างและสุ่มตัวอย่างอย่างอิสระจากประชากร

ตราบใดที่ใช้ วิธีการสุ่มตัวอย่างความน่าจะเป็น (สมาชิกแต่ละคนในประชากรมีความน่าจะเป็นเท่ากันในการเลือกให้อยู่ในกลุ่มตัวอย่าง) เพื่อรวบรวมข้อมูล เราสามารถสรุปได้ว่าการสังเกตแต่ละครั้งถูกสุ่มตัวอย่างในลักษณะสุ่มและเป็นอิสระ

ตัวอย่างวิธีการสุ่มตัวอย่างความน่าจะเป็น ได้แก่:

• การสุ่มตัวอย่างอย่างง่าย
• การสุ่มตัวอย่างแบบแบ่งชั้น
• การสุ่มตัวอย่างแบบคลัสเตอร์
• การสุ่มตัวอย่างอย่างเป็นระบบ

สมมติฐานที่ 3: ความแปรปรวนเท่ากัน

MANOVA จะถือว่าเมทริกซ์ความแปรปรวนร่วมประชากรของแต่ละกลุ่มเท่ากัน

วิธีที่ใช้กันทั่วไปในการทดสอบสมมติฐานนี้คือการใช้การทดสอบ M ของ Box เป็นที่ทราบกันว่าการทดสอบนี้ค่อนข้างเข้มงวด ซึ่งเป็นเหตุผลว่าทำไมเราจึงใช้ระดับนัยสำคัญที่ 0.001 เพื่อพิจารณาว่าเมทริกซ์ความแปรปรวนร่วมของประชากรเท่ากันหรือไม่

หากค่า p ของการทดสอบ M ของ Box มากกว่า 0.001 เราสามารถสรุปได้ว่าเป็นไปตามสมมติฐานนี้

โชคดีที่แม้ว่าค่า p ของการทดสอบจะน้อยกว่า 0.001 แต่ MANOVA ก็มีแนวโน้มที่จะทนทานต่อการเบี่ยงเบนไปจากสมมติฐานนี้

เพื่อให้เมทริกซ์ความแปรปรวนร่วมไม่เท่ากันเป็นปัญหา ความแตกต่างระหว่างเมทริกซ์ความแปรปรวนร่วมจะต้องค่อนข้างรุนแรง

สมมติฐานที่ 4: ไม่มีค่าผิดปกติหลายตัวแปร

MANOVA ถือว่าไม่มีค่าผิดปกติหลายตัวแปรที่รุนแรงในข้อมูลที่อาจส่งผลต่อผลลัพธ์อย่างมีนัยสำคัญ

วิธีที่ใช้กันทั่วไปในการตรวจสอบสมมติฐานนี้คือการคำนวณระยะทางมหาลาโนบิสสำหรับการสังเกตแต่ละครั้ง ซึ่งแสดงถึงระยะห่างระหว่างจุดสองจุดในพื้นที่หลายตัวแปร

หากค่า p ที่สอดคล้องกันสำหรับระยะห่างของมาฮาลาโนบิสของการสังเกตน้อยกว่า 0.001 โดยทั่วไปเราจะประกาศว่าการสังเกตนั้นมีค่าผิดปกติอย่างมาก

ดูบทช่วยสอนต่อไปนี้เพื่อดูวิธีคำนวณระยะทางมหาลาโนบิสในซอฟต์แวร์ทางสถิติต่างๆ:

• วิธีการคำนวณระยะทาง Mahalanobis ใน R
• วิธีการคำนวณระยะทาง Mahalanobis ใน SPSS
• วิธีการคำนวณระยะทาง Mahalanobis ใน Python

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้จะอธิบายวิธีดำเนินการ MANOVA ในซอฟต์แวร์ทางสถิติต่างๆ:

วิธีดำเนินการ MANOVA ใน R
วิธีการดำเนินการ MANOVA ใน SPSS
วิธีดำเนินการ MANOVA ใน Stata