สหสัมพันธ์กับการถดถอย: อะไรคือความแตกต่าง?

สหสัมพันธ์ และ การถดถอย เป็นสองเงื่อนไขที่เกี่ยวข้องกัน แต่ไม่เหมือนกันทั้งหมดในแง่สถิติ

ในบทช่วยสอนนี้ เราจะให้คำอธิบายโดยย่อของคำศัพท์ทั้งสองและอธิบายว่าคำทั้งสองมีความเหมือนและแตกต่างกันอย่างไร

ความสัมพันธ์คืออะไร?

สหสัมพันธ์ จะวัดความสัมพันธ์เชิงเส้นระหว่างตัวแปรสองตัว คือ x และ y มีค่าระหว่าง -1 ถึง 1 โดยที่:

• -1 บ่งชี้ถึงความสัมพันธ์เชิงเส้นเชิงลบอย่างสมบูรณ์ระหว่างตัวแปรสองตัว
• 0 บ่งชี้ว่าไม่มีความสัมพันธ์เชิงเส้นระหว่างตัวแปรสองตัว
• 1 บ่งชี้ความสัมพันธ์เชิงเส้นเชิงบวกอย่างสมบูรณ์ระหว่างตัวแปรสองตัว

ตัวอย่างเช่น สมมติว่าเรามีชุดข้อมูลต่อไปนี้ที่มีตัวแปรสองตัว: (1) ชั่วโมงที่เรียน และ (2) คะแนนสอบที่ได้รับสำหรับนักเรียน 20 คน:

หากเราสร้างแผนภูมิกระจายของชั่วโมงเรียนเทียบกับผลการสอบ หน้าตาจะเป็นอย่างไร:

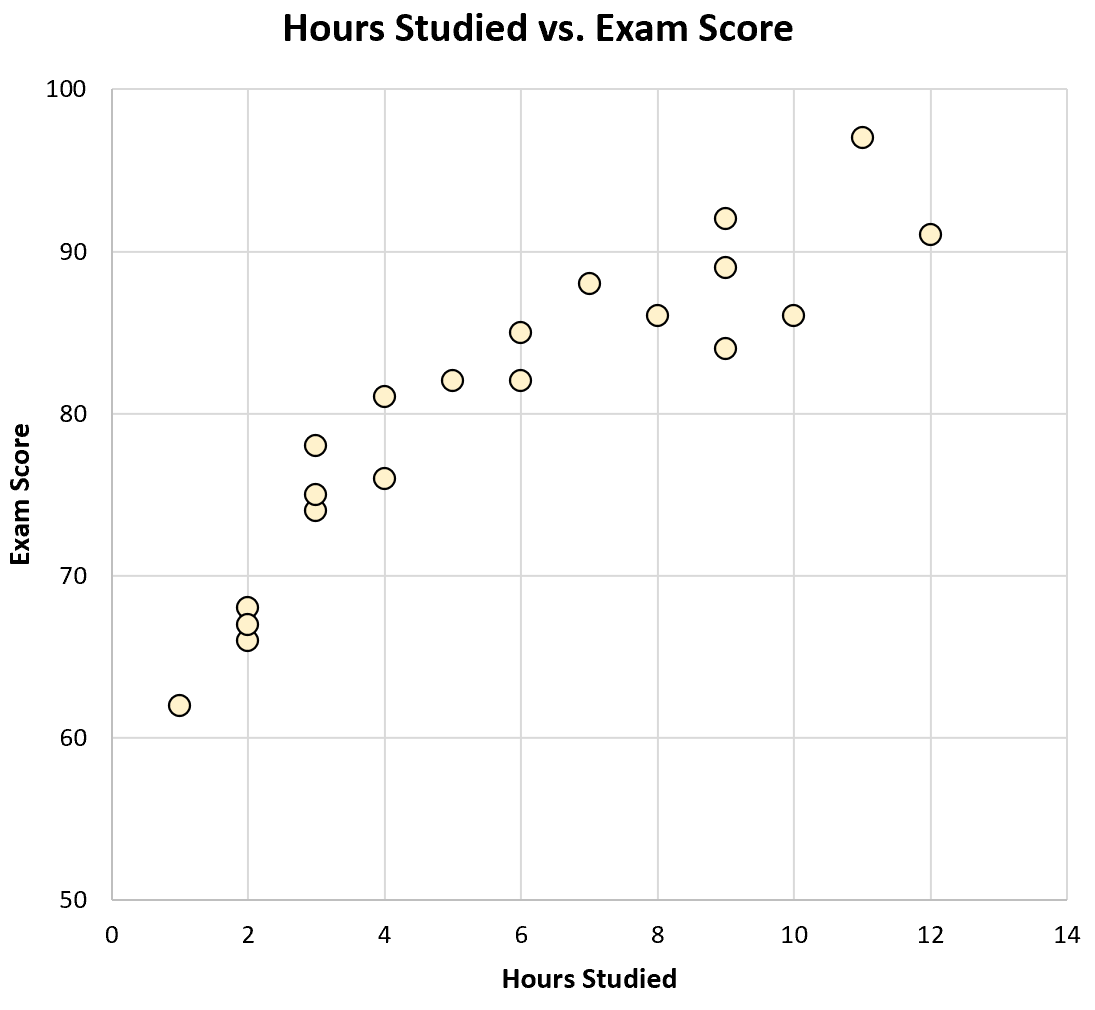
แค่ดูกราฟก็พบว่านักเรียนที่เรียนมากกว่ามักจะทำข้อสอบได้ดีขึ้น กล่าวอีกนัยหนึ่ง เราจะเห็นได้อย่างชัดเจนว่ามี ความสัมพันธ์เชิงบวก ระหว่างตัวแปรทั้งสอง

จากการใช้เครื่องคิดเลข เราจะเห็นว่าความสัมพันธ์ระหว่างตัวแปรทั้งสองนี้คือ r = 0.915 ค่านี้ใกล้กับ 1 เป็นการยืนยันว่ามีความสัมพันธ์เชิงบวกที่แข็งแกร่งระหว่างตัวแปรทั้งสอง

การถดถอยคืออะไร?

การถดถอย เป็นวิธีการที่เราสามารถใช้เพื่อทำความเข้าใจว่าการเปลี่ยนแปลงค่าของตัวแปร x ส่งผลต่อค่าของตัวแปร y อย่างไร

โมเดลการถดถอยใช้ตัวแปรตัวหนึ่ง x เป็นตัวแปรทำนาย และอีกตัวแปร y เป็น ตัวแปรตอบสนอง จากนั้นจะค้นหาสมการในรูปแบบต่อไปนี้ที่อธิบายความสัมพันธ์ระหว่างตัวแปรทั้งสองได้ดีที่สุด:

ŷ = ข ₀ + ข ₁ x

ทอง:

• ŷ: ค่าที่ทำนายไว้ของตัวแปรตอบสนอง
• b ₀ : พิกัดที่จุดกำเนิด (ค่า y เมื่อ x เท่ากับศูนย์)
• b ₁ : ค่าสัมประสิทธิ์การถดถอย (ค่าเฉลี่ยเพิ่มขึ้นใน y สำหรับการเพิ่มขึ้นของ x หนึ่งหน่วย)
• x: ค่าของตัวแปรทำนาย

ตัวอย่างเช่น ลองพิจารณาชุดข้อมูลก่อนหน้าของเรา:

เมื่อใช้ เครื่องคำนวณการถดถอยเชิงเส้น เราพบว่าสมการต่อไปนี้อธิบายความสัมพันธ์ระหว่างตัวแปรทั้งสองนี้ได้ดีที่สุด:

คะแนนสอบที่คาดการณ์ = 65.47 + 2.58*(จำนวนชั่วโมงเรียน)

วิธีการตีความสมการนี้คือ:

• คะแนนสอบที่คาดการณ์ไว้สำหรับนักเรียนที่เรียนเป็นศูนย์ชั่วโมงคือ 65.47
• คะแนนสอบเฉลี่ยที่เพิ่มขึ้นที่เกี่ยวข้องกับชั่วโมงเรียนเพิ่มเติมคือ 2.58

นอกจากนี้เรายังสามารถใช้สมการนี้เพื่อทำนายคะแนนที่นักเรียนจะได้รับตามจำนวนชั่วโมงที่เรียน

เช่น นักเรียนที่เรียน 6 ชั่วโมง ควรได้เกรด 80.95 :

คะแนนสอบที่คาดการณ์ = 65.47 + 2.58*(6) = 80.95

นอกจากนี้เรายังสามารถพลอตสมการนี้เป็นเส้นบนแผนผังกระจายได้:

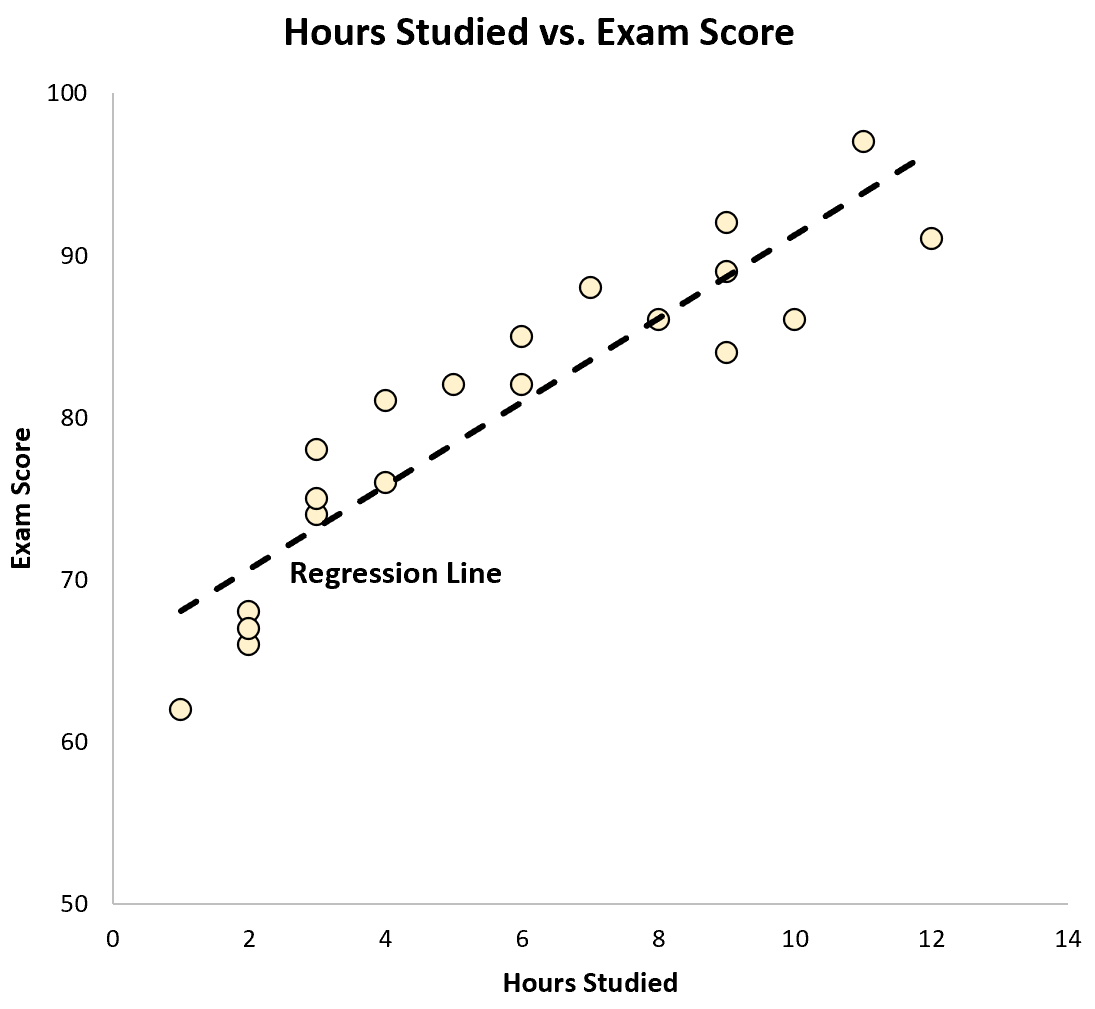
เราจะเห็นว่าเส้นการถดถอย “พอดี” กับข้อมูลค่อนข้างดี

จำได้ก่อนหน้านี้ว่าความสัมพันธ์ระหว่างตัวแปรทั้งสองนี้คือ r = 0.915 ปรากฎว่าเราสามารถยกกำลังสองค่านี้แล้วได้ตัวเลขที่เรียกว่า “r กำลังสอง” ซึ่งอธิบายสัดส่วนรวมของ ความแปรปรวน ในตัวแปรตอบสนองที่สามารถอธิบายได้ด้วยตัวแปรทำนาย

ในตัวอย่างนี้ r ² = 0.915 ² = 0.837 ซึ่งหมายความว่า 83.7% ของความแปรผันของคะแนนสอบสามารถอธิบายได้ด้วยจำนวนชั่วโมงที่เรียน

สหสัมพันธ์กับการถดถอย: ความเหมือนและความแตกต่าง

นี่คือบทสรุปของความเหมือนและความแตกต่างระหว่างสหสัมพันธ์และการถดถอย:

ความเหมือน:

• ทั้งสองวัดปริมาณทิศทางของความสัมพันธ์ระหว่างตัวแปรสองตัว
• ทั้งสองวัดปริมาณความแข็งแกร่งของความสัมพันธ์ระหว่างตัวแปรทั้งสอง

ความแตกต่าง:

• การถดถอยสามารถแสดงความสัมพันธ์ระหว่างเหตุและผลระหว่างตัวแปรสองตัวได้ ความสัมพันธ์ไม่ได้ทำอย่างนั้น
• การถดถอยสามารถใช้สมการเพื่อทำนายค่าของตัวแปรหนึ่ง โดยอิงจากค่าของตัวแปรอีกตัวหนึ่งได้ ความสัมพันธ์ไม่ได้ทำอย่างนั้น
• การถดถอยใช้สมการเพื่อหาปริมาณความสัมพันธ์ระหว่างตัวแปรสองตัว ความสัมพันธ์ใช้ตัวเลขตัวเดียว

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้นำเสนอคำอธิบายเชิงลึกเพิ่มเติมของหัวข้อที่กล่าวถึงในบทความนี้

ความรู้เบื้องต้นเกี่ยวกับสัมประสิทธิ์สหสัมพันธ์เพียร์สัน
ความรู้เบื้องต้นเกี่ยวกับการถดถอยเชิงเส้นอย่างง่าย
เครื่องคำนวณการถดถอยเชิงเส้นอย่างง่าย
ค่า R-กำลังสองที่ดีคืออะไร?