ส่วนเบี่ยงเบนมาตรฐานเสมือน

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 3, 2023 สถิติ 0 ความคิดเห็น

บทความนี้จะอธิบายว่าค่าเบี่ยงเบนมาตรฐานเสมือนในสถิติคืออะไร และวิธีการคำนวณ ดังนั้นคุณจะพบสูตรค่าเบี่ยงเบนมาตรฐานเสมือน แบบฝึกหัดแก้โจทย์ และนอกจากนี้ เครื่องคิดเลขออนไลน์สำหรับคำนวณค่าเบี่ยงเบนมาตรฐานเสมือนของชุดข้อมูลใดๆ

ค่าเบี่ยงเบนมาตรฐานเสมือนคืออะไร?

ในสถิติ ค่าเบี่ยงเบนมาตรฐานเสมือน เป็นหน่วยวัดการกระจายตัวที่บ่งบอกถึงความแปรปรวนของกลุ่มตัวอย่าง โดยเฉพาะอย่างยิ่ง ค่าเบี่ยงเบนมาตรฐานเสมือนเท่ากับรากที่สองของผลรวมของกำลังสองของการเบี่ยงเบนหารด้วยจำนวนจุดข้อมูลทั้งหมดลบด้วยหนึ่ง

สัญลักษณ์ของค่าเบี่ยงเบนมาตรฐานเสมือนคือ σ _n-1 os _n-1

ค่าเบี่ยงเบนมาตรฐานเสมือนอาจเรียกว่า ค่าเบี่ยงเบนมาตรฐานเสมือน และบางครั้งเรียกว่าค่าเบี่ยงเบนมาตรฐานตัวอย่าง เนื่องจากโดยปกติจะคำนวณโดยใช้ค่าจากตัวอย่างทางสถิติ ด้านล่างนี้เราจะลงรายละเอียดเกี่ยวกับความแตกต่างระหว่างค่าเบี่ยงเบนมาตรฐานและค่าเบี่ยงเบนมาตรฐาน

สูตรส่วนเบี่ยงเบนมาตรฐานเสมือน

ค่าเบี่ยงเบนมาตรฐานเสมือนเท่ากับรากที่สองของผลรวมของกำลังสองของการเบี่ยงเบนของชุดข้อมูล หารด้วยจำนวนการสังเกตทั้งหมดลบด้วยหนึ่ง ดังนั้น สูตรในการคำนวณค่าเบี่ยงเบนมาตรฐานเสมือน คือ:

สูตรค่าเบี่ยงเบนมาตรฐานเสมือน (หรือค่าเบี่ยงเบนมาตรฐานเสมือน)

ทอง:

$\sigma_{n-1}$

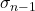
นี่คือค่าเบี่ยงเบนมาตรฐานเสมือน
$x_i$

คือค่าข้อมูล

$i$

.
$n$

คือจำนวนข้อมูลทั้งหมด
$\overline{x}$

คือค่าเฉลี่ยของชุดข้อมูล

👉 คุณสามารถใช้เครื่องคิดเลขด้านล่างเพื่อคำนวณค่าเบี่ยงเบนมาตรฐานเสมือนสำหรับชุดข้อมูลใดก็ได้

ตัวอย่างการคำนวณค่าเบี่ยงเบนมาตรฐานเสมือน

เมื่อพิจารณาคำจำกัดความของค่าเบี่ยงเบนมาตรฐาน คุณสามารถดูตัวอย่างง่ายๆ ของวิธีคำนวณค่าเบี่ยงเบนมาตรฐานของชุดข้อมูลได้ที่ด้านล่างนี้

งบประมาณของบริษัทสำหรับแผนกวิจัยและพัฒนามีความผันผวนมาก เนื่องจากขึ้นอยู่กับกำไรทางเศรษฐกิจที่บริษัทได้รับในปีที่แล้ว ดังนั้นงบประมาณสำหรับส่วนนี้ในช่วงห้าปีที่ผ่านมาคือ: 3, 6, 2, 9, 4 ล้านยูโร คำนวณค่าเบี่ยงเบนเสมือนมาตรฐานของชุดข้อมูลนี้

สิ่งแรกที่เราต้องทำเพื่อกำหนดค่าเบี่ยงเบนมาตรฐานเสมือนคือการคำนวณค่าเฉลี่ยเลขคณิตของกลุ่มตัวอย่าง ในการดำเนินการนี้ เราจะบวกข้อมูลทั้งหมดและหารด้วยจำนวนการสังเกตทั้งหมด ซึ่งก็คือ 5:

$\overline{x}=\cfrac{3+6+2+9+4}{5}=4,8$

ต่อไป เราใช้สูตรส่วนเบี่ยงเบนมาตรฐานกึ่ง:

$\displaystyle\sigma_{n-1}=\sqrt{\frac{\displaystyle\sum_{i=1}^n(x_i-\overline{x})^2}{n-1}}$

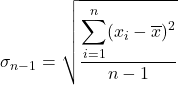
เราแทนที่ข้อมูลลงในสูตร:

$\displaystyle \sigma_{n-1}=\sqrt{\frac{(3-4,8)^2+(6-4,8)^2+(2-4,8)^2+(9-4,8)^2+(4-4,8)^2}{5-1}}$

และสุดท้าย เราก็คำนวณค่าเบี่ยงเบนมาตรฐานเสมือน:

$\begin{aligned}\displaystyle\sigma_{n-1} & = \sqrt{\frac{(-1,8)^2+1,2^2+(-2,8)^2+4,2^2+(-0,8)^2}{5-1}}\\[2ex]&=\sqrt{\frac{3,24+1,44+7,84+17,64+0,64}{4}}\\[2ex]&= \sqrt{\frac{30,8}{4}}=\sqrt{7,7}=2,77 \end{aligned}$

กล่าวโดยสรุป ค่าเบี่ยงเบนมาตรฐานเสมือนของกลุ่มตัวอย่างข้อมูลคือ 2.77 ล้าน

➤ ดู: Quasivariance

เครื่องคำนวณค่าเบี่ยงเบนมาตรฐานเสมือน

เสียบข้อมูลทางสถิติที่ตั้งค่าไว้ในเครื่องคิดเลขออนไลน์ด้านล่างเพื่อคำนวณค่าเบี่ยงเบนเสมือนมาตรฐาน ข้อมูลต้องคั่นด้วยช่องว่างและป้อนโดยใช้จุดเป็นตัวคั่นทศนิยม

ส่วนเบี่ยงเบนมาตรฐานเสมือนและส่วนเบี่ยงเบนมาตรฐาน

สุดท้ายนี้ เราจะเห็นว่าความแตกต่างระหว่างค่าเบี่ยงเบนมาตรฐานและค่าเบี่ยงเบนมาตรฐานคืออะไร เนื่องจากเป็นหน่วยวัดทางสถิติที่แตกต่างกันสองรายการที่มีชื่อคล้ายกันมากและคำนวณด้วยวิธีที่คล้ายกันมาก

ความแตกต่างระหว่างส่วนเบี่ยงเบนมาตรฐานเสมือนและส่วนเบี่ยงเบนมาตรฐาน คือตัวส่วนของสูตร ในการคำนวณค่าเบี่ยงเบนมาตรฐานเสมือน ให้หารด้วย n-1 แต่ค่าเบี่ยงเบนมาตรฐานคำนวณโดยการหารด้วย n

ดังนั้น ค่าเบี่ยงเบนมาตรฐานเสมือนและค่าเบี่ยงเบนมาตรฐานจึงมีความสัมพันธ์กันทางคณิตศาสตร์ เนื่องจากค่าเบี่ยงเบนมาตรฐานเสมือนเทียบเท่ากับค่าเบี่ยงเบนมาตรฐานคูณด้วยรากที่สองของ n (จำนวนจุดข้อมูลทั้งหมด) ส่วน n-1

$\displaystyle\sigma_{n-1}=\sqrt{\frac{n}{n-1}}\cdot \sigma$

จากสมการก่อนหน้านี้ เราสามารถสรุปได้ว่า สำหรับข้อมูลชุดเดียวกัน ค่าของส่วนเบี่ยงเบนมาตรฐานเสมือนจะมากกว่าค่าของส่วนเบี่ยงเบนมาตรฐานเสมอ

นอกจากนี้ สูตรค่าเบี่ยงเบนมาตรฐานเสมือนมักใช้ในการคำนวณค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่าง เนื่องจากจะขจัดอคติ ค่าเบี่ยงเบนมาตรฐานกึ่งจึงเป็นตัวประมาณที่ดีของค่าเบี่ยงเบนมาตรฐานของประชากร ด้วยเหตุนี้ เมื่อทำการอนุมานทางสถิติจากตัวอย่าง จึงเป็นเรื่องปกติที่จะบอกว่าค่าเบี่ยงเบนมาตรฐานถูกคำนวณ แต่ในความเป็นจริงแล้ว ค่าเบี่ยงเบนมาตรฐานถูกคำนวณ

➤ ดูที่: คุณสมบัติของส่วนเบี่ยงเบนมาตรฐาน

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม