การวิเคราะห์ความแปรปรวนแบบทางเดียว: คำจำกัดความ สูตร และตัวอย่าง
การวิเคราะห์ ความแปรปรวนแบบทางเดียว (“การวิเคราะห์ความแปรปรวน”) จะเปรียบเทียบค่าเฉลี่ยของกลุ่มอิสระตั้งแต่ 3 กลุ่มขึ้นไป เพื่อพิจารณาว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างค่าเฉลี่ยของประชากรที่เกี่ยวข้องหรือไม่
บทช่วยสอนนี้จะอธิบายสิ่งต่อไปนี้:
- แรงจูงใจในการดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียว
- สมมติฐานที่ต้องปฏิบัติตามเพื่อทำการวิเคราะห์ความแปรปรวนแบบทางเดียว
- กระบวนการดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียว
- ตัวอย่างวิธีดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียว
การวิเคราะห์ความแปรปรวนแบบทางเดียว: แรงจูงใจ
สมมติว่าเราต้องการทราบว่าโปรแกรมเตรียมสอบสามโปรแกรมที่แตกต่างกันนำไปสู่คะแนนเฉลี่ยที่แตกต่างกันในการสอบเข้าวิทยาลัยหรือไม่ เนื่องจากมีนักเรียนมัธยมปลายหลายล้านคนทั่วประเทศ จึงอาจใช้เวลานานและมีราคาแพงเกินไปที่จะให้นักเรียนทุกคนใช้โปรแกรมเตรียมสอบโปรแกรมใดโปรแกรมหนึ่ง
แต่เราสามารถเลือก สุ่มตัวอย่างสามตัวอย่าง จากนักเรียน 100 คนจากประชากร และอนุญาตให้แต่ละตัวอย่างใช้โปรแกรมเตรียมสอบหนึ่งในสามโปรแกรมเพื่อเตรียมตัวสำหรับการสอบ จากนั้นเราจะบันทึกคะแนนของนักเรียนแต่ละคนเมื่อทำข้อสอบได้
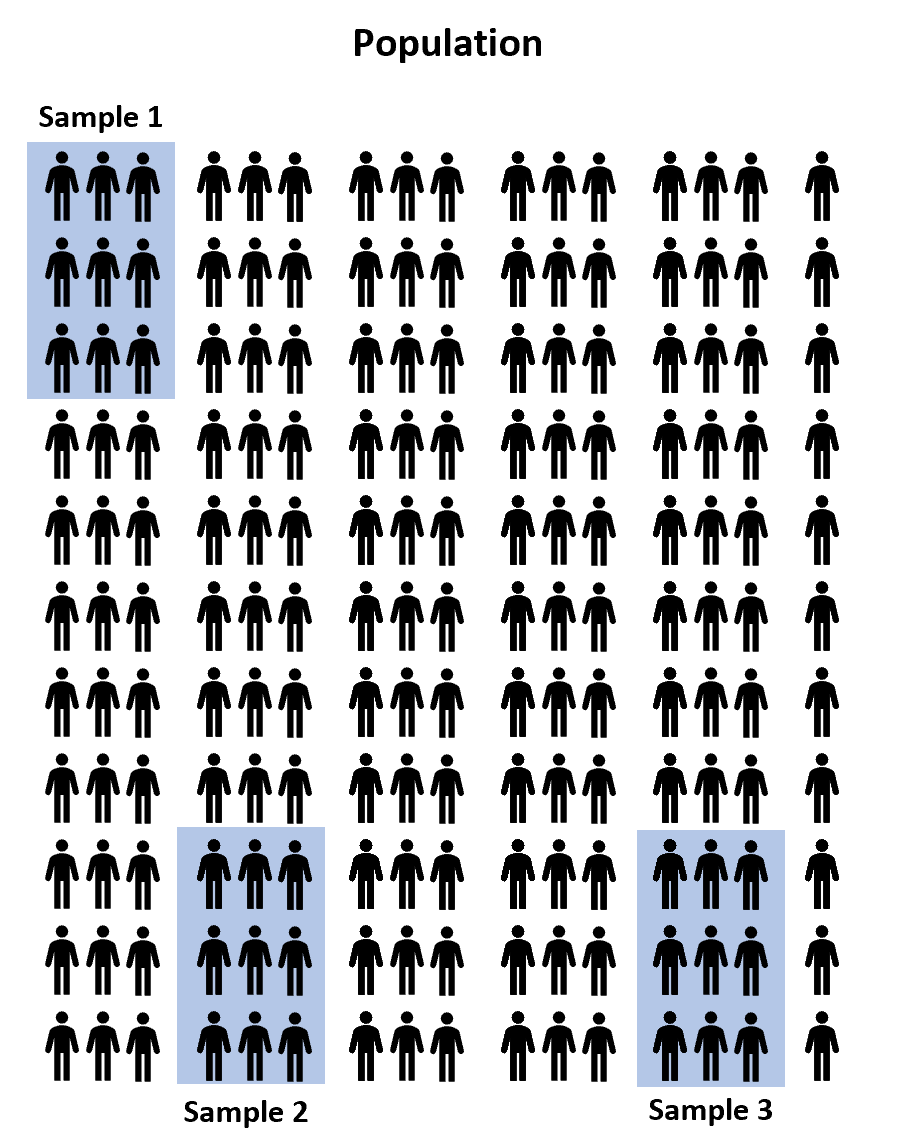
อย่างไรก็ตาม รับประกันได้เลยว่าคะแนนสอบเฉลี่ยระหว่างตัวอย่างทั้งสามจะแตกต่างกันเล็กน้อยเป็นอย่างน้อย คำถามคือความแตกต่างนี้มีนัยสำคัญทางสถิติหรือไม่ โชคดีที่การวิเคราะห์ความแปรปรวนแบบทางเดียวช่วยให้เราสามารถตอบคำถามนี้ได้
การวิเคราะห์ความแปรปรวนแบบทางเดียว: สมมติฐาน
เพื่อให้ผลลัพธ์ของการวิเคราะห์ความแปรปรวนแบบทางเดียวถูกต้อง ต้องเป็นไปตามสมมติฐานต่อไปนี้:
1. ความปกติ – แต่ละตัวอย่างดึงมาจากประชากรที่แจกแจงตามปกติ
2. ความแปรปรวนที่เท่ากัน – ความแปรปรวนของประชากรที่ใช้สุ่มตัวอย่างเท่ากัน คุณสามารถใช้ การทดสอบของ Bartlett เพื่อทดสอบสมมติฐานนี้ได้
3. ความเป็นอิสระ – การสังเกตภายในแต่ละกลุ่มมีความเป็นอิสระจากกันและการสังเกตภายในกลุ่มได้โดยการสุ่มตัวอย่าง
อ่าน บทความนี้ เพื่อดูรายละเอียดเพิ่มเติมเกี่ยวกับวิธีการตรวจสอบสมมติฐานเหล่านี้
การวิเคราะห์ความแปรปรวนแบบทางเดียว: กระบวนการ
การวิเคราะห์ความแปรปรวนทางเดียวใช้สมมติฐานว่างและทางเลือกต่อไปนี้:
- H 0 (สมมติฐานว่าง): μ 1 = μ 2 = μ 3 = … = μ k (ค่าเฉลี่ยประชากรทั้งหมดเท่ากัน)
- H 1 (สมมติฐานทางเลือก): ค่าเฉลี่ยประชากรอย่างน้อย 1 รายการแตกต่างกัน พักผ่อน
โดยทั่วไปคุณจะใช้ซอฟต์แวร์ทางสถิติบางอย่าง (เช่น R, Excel, Stata, SPSS เป็นต้น) เพื่อทำการวิเคราะห์ความแปรปรวนแบบทางเดียว เนื่องจากการดำเนินการด้วยตนเองนั้นน่าเบื่อ
ไม่ว่าคุณจะใช้ซอฟต์แวร์ใดก็ตาม คุณจะได้รับตารางต่อไปนี้เป็นเอาต์พุต:
| แหล่งที่มา | ผลรวมของกำลังสอง (SS) | df | ค่าเฉลี่ยกำลังสอง (MS) | เอฟ | พี |
|---|---|---|---|---|---|
| การรักษา | อาร์เอสเอส | df อาร์ | เอ็มเอสอาร์ | MSR/MSE | ฟ ฟ ร , df อี |
| ข้อผิดพลาด | เอสเอส | df อี | มสธ | ||
| ทั้งหมด | โอ้โฮ | df เสื้อ |
ทอง:
- SSR: ผลรวมของการถดถอยกำลังสอง
- SSE: ผลรวมของความคลาดเคลื่อนกำลังสอง
- SST: ผลรวมของกำลังสอง (SST = SSR + SSE)
- df r : องศาความเป็นอิสระของการถดถอย (df r = k-1)
- df e : องศาความคลาดเคลื่อนของเสรีภาพ (df e = nk)
- df t : องศาอิสระทั้งหมด (df t = n-1)
- k: จำนวนกลุ่มทั้งหมด
- n: การสังเกตทั้งหมด
- MSR: การถดถอยกำลังสองเฉลี่ย (MSR = SSR/df r )
- MSE: ค่าคลาดเคลื่อนกำลังสองเฉลี่ย (MSE = SSE/df e )
- F: สถิติการทดสอบ F (F = MSR/MSE)
- p: ค่า p ซึ่งสอดคล้องกับ F dfr, dfe
ถ้าค่า p น้อยกว่าระดับนัยสำคัญที่เลือก (เช่น 0.05) คุณสามารถปฏิเสธสมมติฐานว่างและสรุปได้ว่าค่าเฉลี่ยประชากรอย่างน้อยหนึ่งค่าแตกต่างจากค่าเฉลี่ยอื่นๆ
หมายเหตุ: ถ้าคุณปฏิเสธสมมติฐานว่าง แสดงว่าค่าเฉลี่ยประชากรอย่างน้อยหนึ่งค่าแตกต่างจากค่าอื่นๆ แต่ตาราง ANOVA ไม่ได้ระบุว่าค่าเฉลี่ยประชากร ใด แตกต่าง ในการระบุสิ่งนี้ คุณจะต้องทำการ ทดสอบหลังการทดสอบ หรือที่เรียกว่าการทดสอบ “การเปรียบเทียบหลายรายการ”
การวิเคราะห์ความแปรปรวนแบบทางเดียว: ตัวอย่าง
สมมติว่าเราต้องการทราบว่าโปรแกรมเตรียมสอบสามโปรแกรมที่แตกต่างกันนำไปสู่คะแนนเฉลี่ยที่แตกต่างกันในการสอบที่กำหนดหรือไม่ เพื่อทดสอบสิ่งนี้ เรารับสมัครนักเรียน 30 คนเพื่อเข้าร่วมในการศึกษาและแบ่งออกเป็นสามกลุ่ม
นักเรียนในแต่ละกลุ่มจะ ได้รับการสุ่มให้ ใช้โปรแกรมเตรียมสอบหนึ่งในสามโปรแกรมสำหรับสามสัปดาห์ต่อจากนี้เพื่อเตรียมตัวสอบ เมื่อสิ้นสุดสามสัปดาห์ นักเรียนทุกคนจะสอบแบบเดียวกัน
ผลการสอบของแต่ละกลุ่มมีดังต่อไปนี้:

หากต้องการดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวกับข้อมูลนี้ เราจะใช้ เครื่องคำนวณความแปรปรวนทางสถิติแบบทางเดียว พร้อมอินพุตต่อไปนี้:

จากตารางผลลัพธ์ เราจะเห็นว่าสถิติการทดสอบ F คือ 2.358 และค่า p ที่สอดคล้องกันคือ 0.11385

เนื่องจากค่า p นี้ไม่น้อยกว่า 0.05 เราจึงไม่สามารถปฏิเสธสมมติฐานว่างได้
ซึ่งหมายความว่า เราไม่มีหลักฐานเพียงพอที่จะบอกว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างคะแนนสอบเฉลี่ยของทั้งสามกลุ่ม
แหล่งข้อมูลเพิ่มเติม
บทความต่อไปนี้จะอธิบายวิธีดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวโดยใช้ซอฟต์แวร์ทางสถิติต่างๆ:
วิธีการดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวใน Excel
วิธีดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวใน R
วิธีการดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวใน Python
วิธีดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวใน SAS
วิธีการดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวใน SPSS
วิธีดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวใน Stata
วิธีดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวบนเครื่องคิดเลข TI-84
เครื่องคำนวณความแปรปรวนแบบทางเดียวออนไลน์