การเปรียบเทียบคะแนน z ของการแจกแจงแบบต่างๆ
คะแนน z จะบอกคุณว่าค่าข้อมูลแต่ละรายการตกจากค่าเฉลี่ยเป็นจำนวนเท่าใด มีการคำนวณดังนี้:
คะแนน z = (x – μ) / σ
ทอง:
- x: ค่าข้อมูลแต่ละรายการ
- μ: ค่าเฉลี่ยประชากร
- σ: ส่วนเบี่ยงเบนมาตรฐานประชากร
คะแนน z สำหรับแต่ละค่าสามารถตีความได้ดังนี้:
- คะแนน z เชิงบวก: ค่าแต่ละค่าสูงกว่าค่าเฉลี่ย
- คะแนน z เชิงลบ: ค่าแต่ละรายการต่ำกว่าค่าเฉลี่ย
- คะแนน z เท่ากับ 0: ค่าแต่ละค่าเท่ากับค่าเฉลี่ย
คะแนน Z มีประโยชน์อย่างยิ่งเมื่อเราต้องการเปรียบเทียบตำแหน่งสัมพัทธ์ของจุดข้อมูลสองจุดจากการแจกแจงสองแบบที่แตกต่างกัน เพื่ออธิบายสิ่งนี้ ให้พิจารณาตัวอย่างต่อไปนี้
ตัวอย่าง: การเปรียบเทียบคะแนน Z
โดยทั่วไปคะแนนในการสอบเข้าวิทยาลัยบางแห่งจะแจกแจงโดยมีค่าเฉลี่ย μ = 80 และส่วนเบี่ยงเบนมาตรฐาน σ = 4 ดวนได้คะแนน 84 ในการสอบนี้
โดยปกติแล้วคะแนนในการสอบระดับวิทยาลัยอื่นจะแจกแจงโดยมีค่าเฉลี่ย μ = 85 และส่วนเบี่ยงเบนมาตรฐาน σ = 8 เด๊บบีได้คะแนน 90 จากการสอบครั้งนั้น
เมื่อเทียบกับการแจกแจงคะแนนสอบของตนเอง ใครทำข้อสอบได้ดีที่สุด?
เพื่อตอบคำถามนี้ เราสามารถคำนวณคะแนน z ของคะแนนสอบของแต่ละคนได้:
คะแนน z ของ Duane = (x – μ) / σ = (84 – 80) / 4 = 4/4 = 1
คะแนน z ของ Debbie = (x – μ) / σ = (90 – 85) / 8 = 5/8 = 0.625
Debbie แม้ว่าคะแนนจะสูงกว่า แต่คะแนนของ Duane ก็สูงกว่าจริง ๆ เมื่อเทียบกับการกระจายข้อสอบเฉพาะของเขา
เพื่อให้เข้าใจสิ่งนี้ ช่วยให้เห็นภาพสถานการณ์ได้ นี่คือคะแนนของ Duane เมื่อเทียบกับคะแนนสอบของเขา:
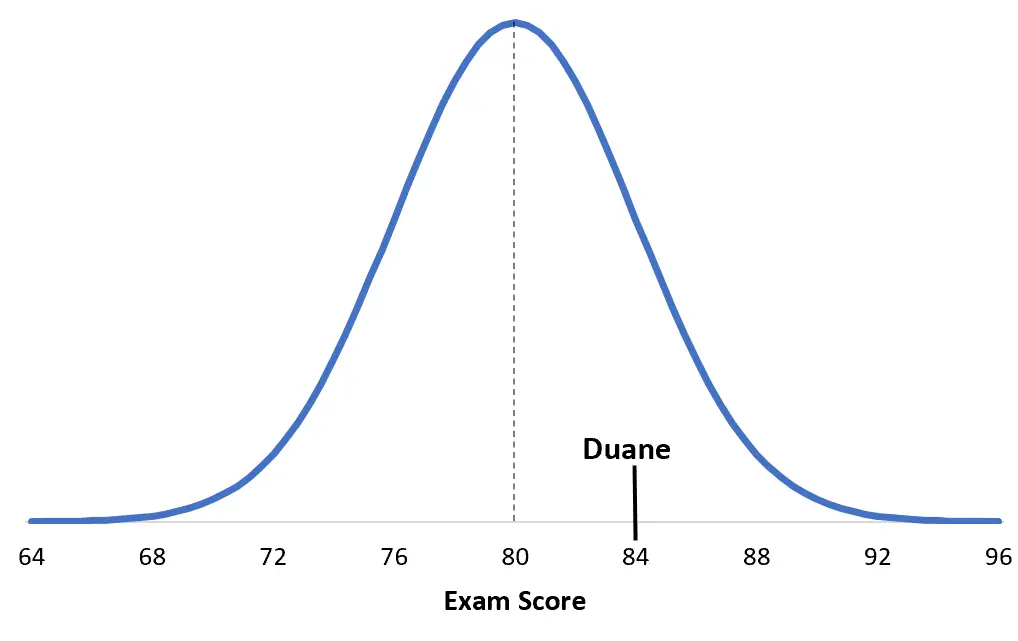
และนี่คือคะแนนของเด็บบีจากการแบ่งข้อสอบของเธอ:
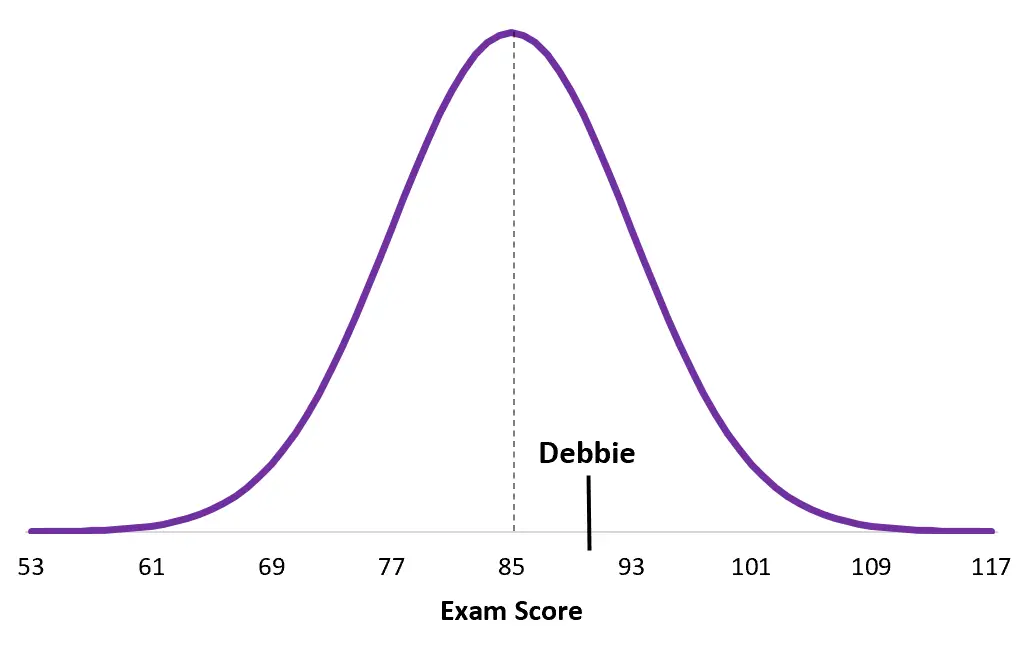
สังเกตว่าคะแนนของเด็บบีใกล้เคียงกับค่าเฉลี่ยประชากรของเธอมากกว่าคะแนนของดวนมากน้อยเพียงใด แม้ว่าเธอจะมีคะแนนโดยรวมที่สูงกว่า แต่คะแนน z ของเธอก็ต่ำกว่าเพียงเพราะคะแนนเฉลี่ยในการสอบเฉพาะของเธอนั้นสูงกว่า
ตัวอย่างนี้แสดงให้เห็นว่าเหตุใดคะแนน z จึงมีประโยชน์มากในการเปรียบเทียบค่าข้อมูลจากการแจกแจงที่แตกต่างกัน คะแนน z คำนึงถึงค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานของการแจกแจงซึ่งช่วยให้เราสามารถเปรียบเทียบค่าข้อมูลจากการแจกแจงที่แตกต่างกันและดูว่ามีค่าใด สูงกว่าเมื่อเปรียบเทียบกับการกระจายตัวของตนเอง
แหล่งข้อมูลเพิ่มเติม
เครื่องคิดเลขคะแนน Z
เปรียบเทียบเครื่องคำนวณคะแนน Z