วิธีแปลงข้อมูลใน python (log, square root, cube root)
การทดสอบทางสถิติจำนวนมากถือว่าชุดข้อมูลมีการกระจายตามปกติ อย่างไรก็ตาม ในทางปฏิบัติมักไม่เป็นเช่นนั้น
วิธีหนึ่งในการแก้ปัญหานี้คือการแปลงการกระจายค่าในชุดข้อมูลโดยใช้การแปลงแบบใดแบบหนึ่งจากสามแบบ:
1. การแปลงบันทึก: แปลงตัวแปรการตอบสนองจาก y เป็น log(y)
2. การแปลงรากที่สอง: แปลงตัวแปรตอบสนองจาก y เป็น √y
3. การแปลงรากที่สาม: แปลงตัวแปรการตอบสนองจาก y เป็น y 1/3
เมื่อทำการแปลงเหล่านี้ ชุดข้อมูลจะมีการกระจายตามปกติมากขึ้น
ตัวอย่างต่อไปนี้แสดงวิธีการแปลงข้อมูลเหล่านี้ใน Python
บันทึกการแปลงใน Python
รหัสต่อไปนี้แสดงวิธีการ แปลงลอการิทึม ในตัวแปรและสร้างการลงจุดแบบเคียงข้างกันเพื่อแสดงการกระจายดั้งเดิมและการกระจายข้อมูลที่แปลงรูปแบบบันทึก:
import numpy as np import matplotlib. pyplot as plt #make this example reproducible n.p. random . seeds (0) #create beta distributed random variable with 200 values data = np. random . beta (a= 4 , b= 15 , size= 300 ) #create log-transformed data data_log = np. log (data) #define grid of plots fig, axs = plt. subplots (nrows= 1 , ncols= 2 ) #create histograms axs[0]. hist (data, edgecolor=' black ') axs[1]. hist (data_log, edgecolor=' black ') #add title to each histogram axs[0]. set_title (' Original Data ') axs[1].set_title(' Log-Transformed Data ')
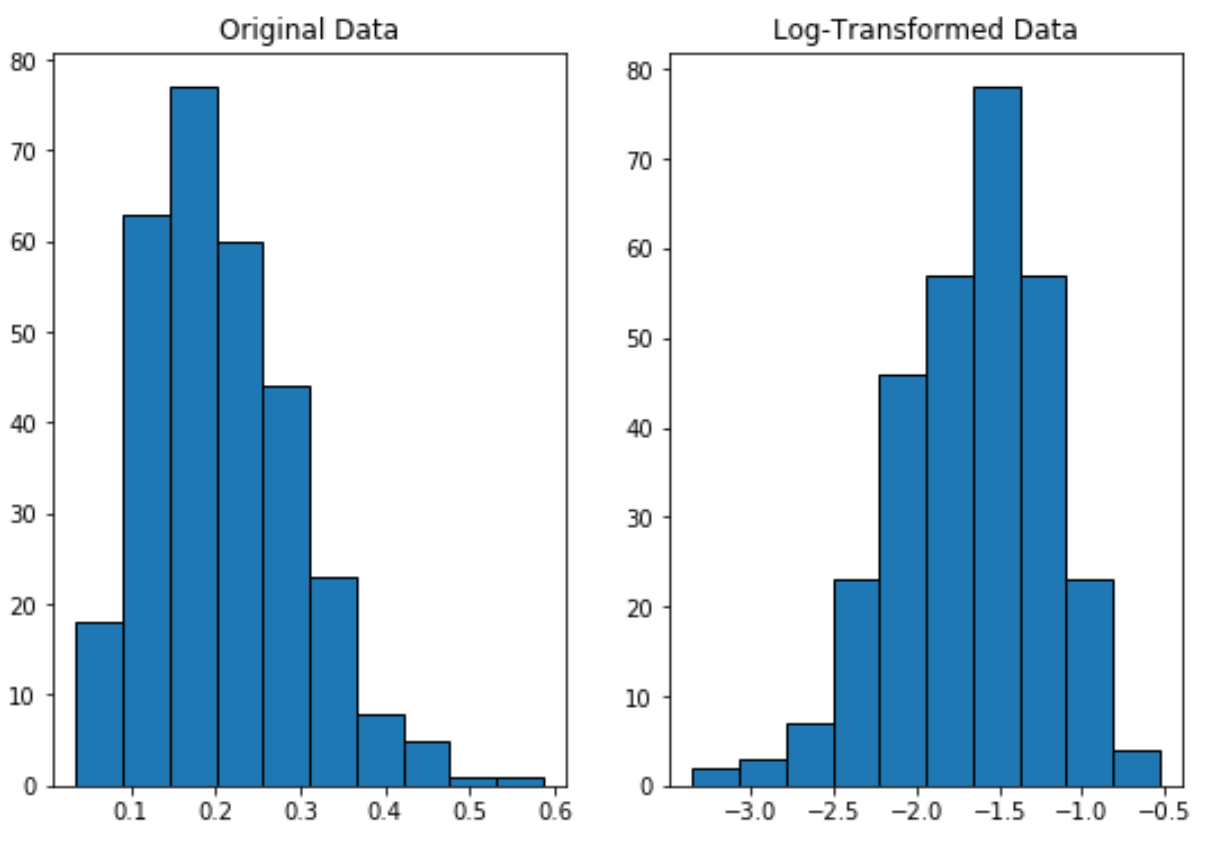
สังเกตว่าการแจกแจงที่แปลงบันทึกนั้นมีการกระจายแบบปกติมากกว่าการแจกแจงดั้งเดิมอย่างไร
มันยังไม่ใช่ “รูปทรงระฆัง” ที่สมบูรณ์แบบแต่มีความใกล้เคียงกับการกระจายตัวแบบปกติมากกว่าการกระจายตัวแบบเดิม
การแปลงรากที่สองใน Python
รหัสต่อไปนี้แสดงวิธีการดำเนิน การแปลงรากที่สอง บนตัวแปรและสร้างการลงจุดแบบเคียงข้างกันเพื่อแสดงการกระจายดั้งเดิมและการกระจายการแปลงรากที่สองของข้อมูล:
import numpy as np import matplotlib. pyplot as plt #make this example reproducible n.p. random . seeds (0) #create beta distributed random variable with 200 values data = np. random . beta (a= 1 , b= 5 , size= 300 ) #create log-transformed data data_log = np. sqrt (data) #define grid of plots fig, axs = plt. subplots (nrows= 1 , ncols= 2 ) #create histograms axs[0]. hist (data, edgecolor=' black ') axs[1]. hist (data_log, edgecolor=' black ') #add title to each histogram axs[0]. set_title (' Original Data ') axs[1].set_title(' Square Root Transformed Data ')
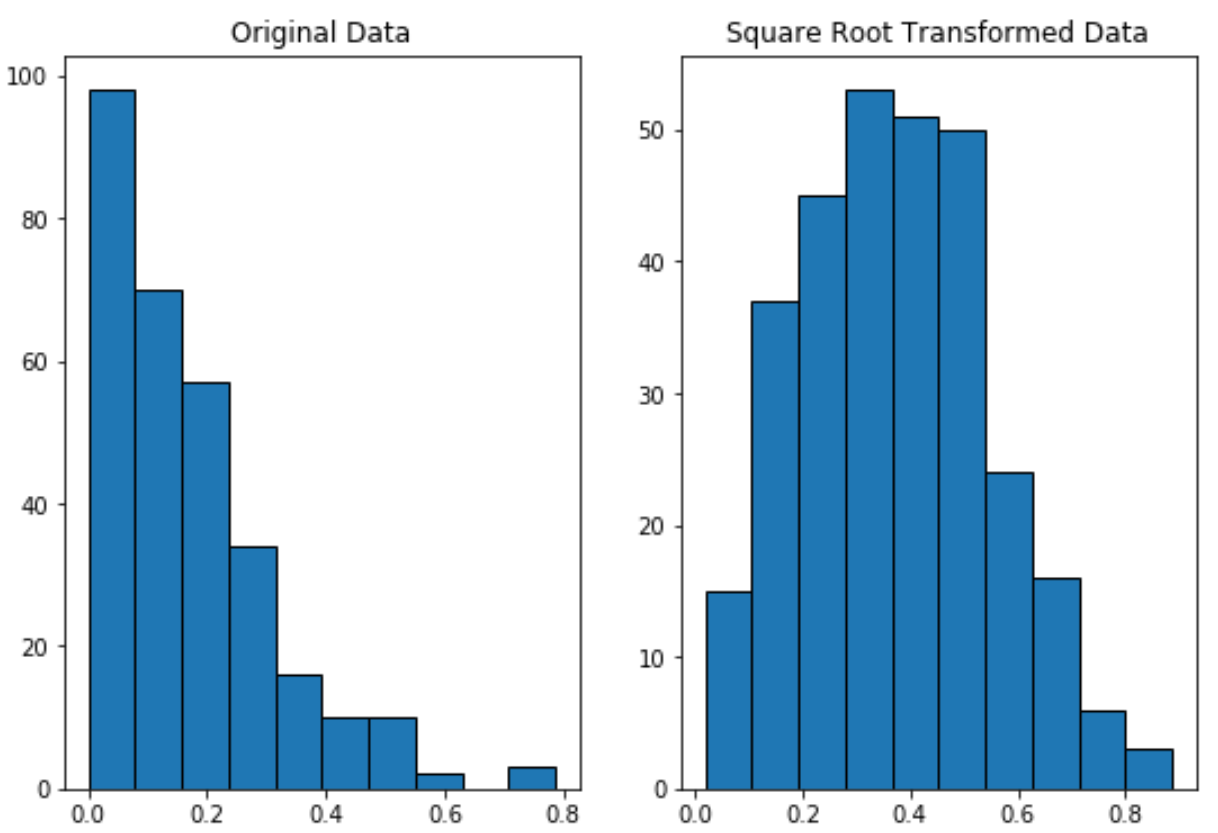
สังเกตว่าข้อมูลที่แปลงรากที่สองนั้นมีการกระจายแบบปกติมากกว่าข้อมูลดั้งเดิมอย่างไร
การแปลงรูทคิวบ์ใน Python
รหัสต่อไปนี้แสดงวิธีการดำเนิน การแปลงรากของคิวบ์ บนตัวแปรและสร้างการลงจุดแบบเคียงข้างกันเพื่อแสดงการแจกแจงแบบเดิมและการกระจายแบบแปลงรากของคิวบ์ของข้อมูล:
import numpy as np import matplotlib. pyplot as plt #make this example reproducible n.p. random . seeds (0) #create beta distributed random variable with 200 values data = np. random . beta (a= 1 , b= 5 , size= 300 ) #create log-transformed data data_log = np. cbrt (data) #define grid of plots fig, axs = plt. subplots (nrows= 1 , ncols= 2 ) #create histograms axs[0]. hist (data, edgecolor=' black ') axs[1]. hist (data_log, edgecolor=' black ') #add title to each histogram axs[0]. set_title (' Original Data ') axs[1].set_title(' Cube Root Transformed Data ')
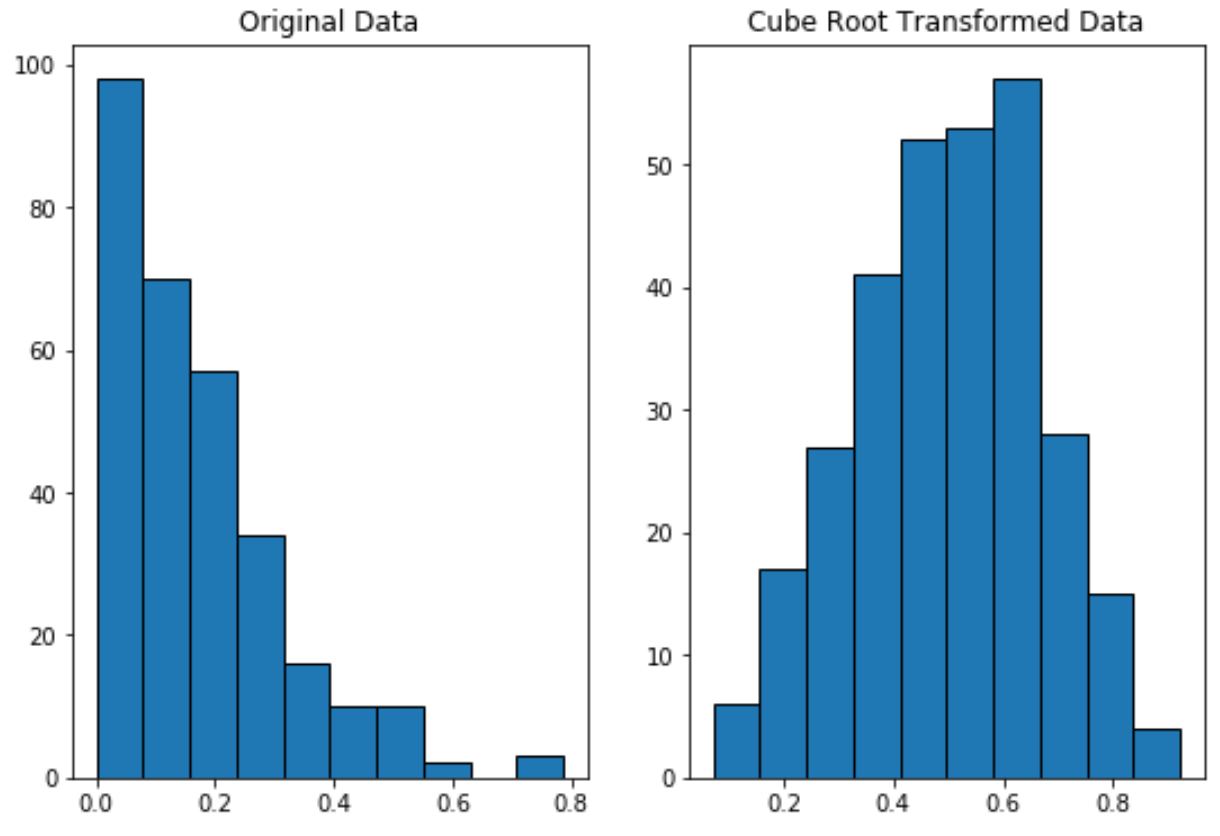
สังเกตว่าข้อมูลที่แปลงรูทของคิวบ์นั้นมีการกระจายตามปกติมากกว่าข้อมูลดั้งเดิมอย่างไร
แหล่งข้อมูลเพิ่มเติม
วิธีคำนวณคะแนน Z ใน Python
วิธีทำให้ข้อมูลเป็นมาตรฐานใน Python
ข้อสันนิษฐานปกติในสถิติคืออะไร?