กฎการบวก (หรือกฎการบวก)

บทความนี้จะอธิบายว่ากฎการบวกหรือที่เรียกว่ากฎการบวกคืออะไร และใช้เพื่ออะไรในความน่าจะเป็นและสถิติ นอกจากนี้ คุณจะสามารถดูได้ว่าสูตรสำหรับกฎการบวกคืออะไร และแบบฝึกหัดที่ได้รับการแก้ไขแล้วจะแสดงวิธีใช้กฎดังกล่าว

กฎการบวก (หรือกฎการบวก) คืออะไร?

กฎการบวก (หรือ กฎการบวก ) ระบุว่าผลรวมของความน่าจะเป็นของสองเหตุการณ์เท่ากับผลรวมของความน่าจะเป็นของแต่ละเหตุการณ์ที่เกิดขึ้นแยกกัน ลบด้วยความน่าจะเป็นของทั้งสองเหตุการณ์ที่เกิดขึ้นในเวลาเดียวกัน

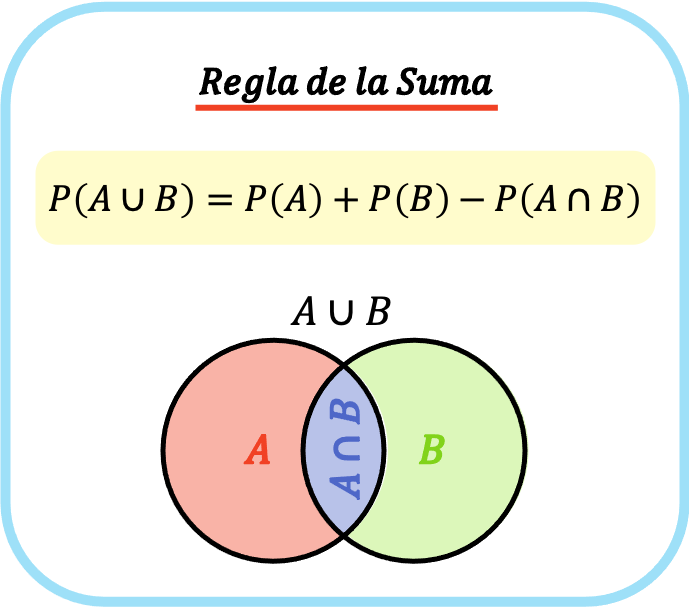
ดังนั้น สูตรสำหรับกฎการบวกคือ P(A⋃B)=P(A)+P(B)−P(A⋂B)

ดังนั้น ในการบวกความน่าจะเป็นสองอย่าง เราไม่สามารถบวกความน่าจะเป็นแต่ละอย่างง่ายๆ ได้ เนื่องจากเราต้องลบคำที่แสดงถึงความน่าจะเป็นร่วมของทั้งสองเหตุการณ์ด้วย อย่างไรก็ตาม ในบางกรณี เพียงแค่เพิ่มความน่าจะเป็นของแต่ละเหตุการณ์เท่านั้นที่เราจะได้ผลลัพธ์ที่ถูกต้องจากผลรวมของความน่าจะเป็น ด้านล่างนี้เราจะดูว่ากรณีเหล่านี้คืออะไร

กล่าวโดยสรุป กฎการเพิ่มใช้ในการคำนวณความน่าจะเป็นของเหตุการณ์หนึ่งหรือเหตุการณ์อื่นที่เกิดขึ้น นั่นคือความน่าจะเป็นที่เหตุการณ์ที่เป็นไปได้อย่างน้อยหนึ่งเหตุการณ์จากสองเหตุการณ์จะเกิดขึ้น

สูตรกฎการบวก

กฎการบวกบอกว่าในการคำนวณความน่าจะเป็นของเหตุการณ์ A หรือเหตุการณ์ B ที่เกิดขึ้น เราต้องบวกความน่าจะเป็นของเหตุการณ์ A ที่เกิดขึ้น บวกกับความน่าจะเป็นของเหตุการณ์ B ที่เกิดขึ้น และลบความน่าจะเป็นที่เหตุการณ์ทั้งสองเกิดขึ้นพร้อมกัน .

สูตรสำหรับกฎการบวก (หรือกฎการบวก) จึงเป็นดังนี้:

ทอง:

• 

  คือความน่าจะเป็นของเหตุการณ์ A หรือเหตุการณ์ B

• 

  คือความน่าจะเป็นที่เหตุการณ์ A จะเกิดขึ้น

• 

  คือความน่าจะเป็นที่เหตุการณ์ B จะเกิดขึ้น

• 

  คือความน่าจะเป็นร่วมที่เหตุการณ์ A และเหตุการณ์ B เกิดขึ้น

ดังนั้น ในการใช้กฎผลรวม คุณจำเป็นต้องรู้วิธีคำนวณความน่าจะเป็นร่วมของสองเหตุการณ์ คุณสามารถดูวิธีการได้ในลิงค์ต่อไปนี้:

ตัวอย่างกฎผลรวมสำหรับกิจกรรมพิเศษ

เพื่อทำความเข้าใจแนวคิดให้เสร็จสิ้น มาดูตัวอย่างวิธีใช้กฎการเพิ่มกัน

• เราใส่ลูกบอลสีน้ำเงิน 10 ลูก ลูกบอลสีส้ม 6 ลูก และลูกบอลสีเขียว 4 ลูกในกล่อง ความน่าจะเป็นที่จะได้ลูกบอลสีน้ำเงินหรือสีส้มเป็นเท่าใด

แบบฝึกหัดนี้ขอให้เราพิจารณาความน่าจะเป็นที่เหตุการณ์ใดเหตุการณ์หนึ่งจะเกิดขึ้น ดังนั้น เพื่อแก้ปัญหา เราจำเป็นต้องใช้สูตรกฎการบวก:

อันดับแรกเราคำนวณความน่าจะเป็นของแต่ละเหตุการณ์ที่เกิดขึ้นแยกกันโดยใช้ กฎของลาปลาซ :

อย่างไรก็ตาม ในกรณีนี้ เหตุการณ์ทั้งสองไม่สามารถเกิดขึ้นพร้อมกันได้ เนื่องจากเป็นสอง เหตุการณ์ที่แยกจากกัน ดังนั้นหากเราวาดลูกบอลสีน้ำเงิน เราก็ไม่สามารถวาดลูกบอลสีส้มได้อีกต่อไป และในทางกลับกัน

ดังนั้น ความน่าจะเป็นร่วมของเหตุการณ์ทั้งสองจึงเป็นศูนย์ และด้วยเหตุนี้ สูตรกฎผลรวมจึงง่ายขึ้น:

ดังนั้นการคำนวณความน่าจะเป็นที่จะได้ลูกบอลสีน้ำเงินหรือลูกบอลสีส้มจึงเป็นดังนี้:

สรุปความน่าจะเป็นที่จะหยิบลูกบอลสีน้ำเงินหรือสีส้มออกจากกล่องคือ 80%

ตัวอย่างกฎการผนวกสำหรับเหตุการณ์ที่ไม่ผูกขาด

เมื่อได้เห็นตัวอย่างที่เป็นรูปธรรมของกฎการเพิ่มเมื่อเหตุการณ์ไม่ผูกขาดแล้ว ตอนนี้เราจะมาดูกันว่ากฎหมายนี้นำไปใช้อย่างไรเมื่อเหตุการณ์ไม่ผูกขาด

• ถ้าเราโยนเหรียญสองครั้ง ความน่าจะเป็นที่จะได้หัวอย่างน้อยหนึ่งครั้งเป็นเท่าใด?

ในกรณีนี้ เหตุการณ์ต่างๆ จะไม่แยกจากกัน เนื่องจากเราสามารถได้ “หัว” ในการโยนครั้งแรกและ “ก้อย” ในการโยนครั้งที่สอง สูตรสำหรับกฎการบวกจึงไม่ซับซ้อนและเป็นดังนี้:

ดังนั้น ก่อนอื่นเราต้องคำนวณความน่าจะเป็นที่จะได้ “หัว” จากการโยนเหรียญโดยใช้กฎของลาปลาซ:

นอกจากนี้ ทั้งสองเหตุการณ์เป็นอิสระต่อกัน ดังนั้นเราจึงสามารถคำนวณความน่าจะเป็นร่วมของทั้งสองเหตุการณ์ได้โดยใช้ กฎผลคูณ :

สุดท้าย หากต้องการค้นหาความน่าจะเป็นที่หัวจะตกในการโยนอย่างน้อยหนึ่งในสองครั้ง เพียงแทนค่าลงในสูตรกฎการบวกแล้วทำการคำนวณ:

โดยสรุป ความน่าจะเป็นที่โยนเหรียญสองครั้งจะขึ้นหัวอย่างน้อยหนึ่งครั้งคือ 75%