ความรู้เบื้องต้นเกี่ยวกับการกระจายเครื่องแบบ

การแจกแจงแบบสม่ำเสมอ คือการแจกแจงความน่าจะเป็นโดยแต่ละค่าระหว่างช่วงจาก a ถึง b มีความน่าจะเป็นที่จะเกิดขึ้นเท่ากัน

หาก ตัวแปรสุ่ม X เป็นไปตามการแจกแจงแบบสม่ำเสมอ ความน่าจะเป็นที่ X รับค่าระหว่าง x ₁ ถึง x ₂ สามารถพบได้โดยใช้สูตรต่อไปนี้:

P(x ₁ < X < x ₂ ) = (x ₂ – x ₁ ) / (b – a)

ทอง:

• x ₁ : มูลค่าดอกเบี้ยที่ต่ำกว่า
• x ₂ : มูลค่าบนของดอกเบี้ย
• a: ค่าต่ำสุดที่เป็นไปได้
• b: ค่าสูงสุดที่เป็นไปได้

ตัวอย่างเช่น สมมติว่าน้ำหนักของโลมามีการกระจายเท่าๆ กันระหว่าง 100 ถึง 150 ปอนด์

หากเราเลือกโลมาโดยการสุ่ม เราสามารถใช้สูตรด้านบนเพื่อหาความน่าจะเป็นที่โลมาที่เลือกจะมีน้ำหนักระหว่าง 120 ถึง 130 ปอนด์:

• ป(120 < X < 130) = (130 – 120) / (150 – 100)
• ป(120 < X < 130) = 10/50
• ป(120 < X < 130) = 0.2

ความน่าจะเป็นที่โลมาที่เลือกจะมีน้ำหนักระหว่าง 120 ถึง 130 ปอนด์ คือ 0.2

เห็นภาพการกระจายตัวที่สม่ำเสมอ

หากเราสร้างแผนภาพความหนาแน่นเพื่อแสดงภาพการกระจายตัวแบบสม่ำเสมอ มันจะมีลักษณะดังต่อไปนี้:

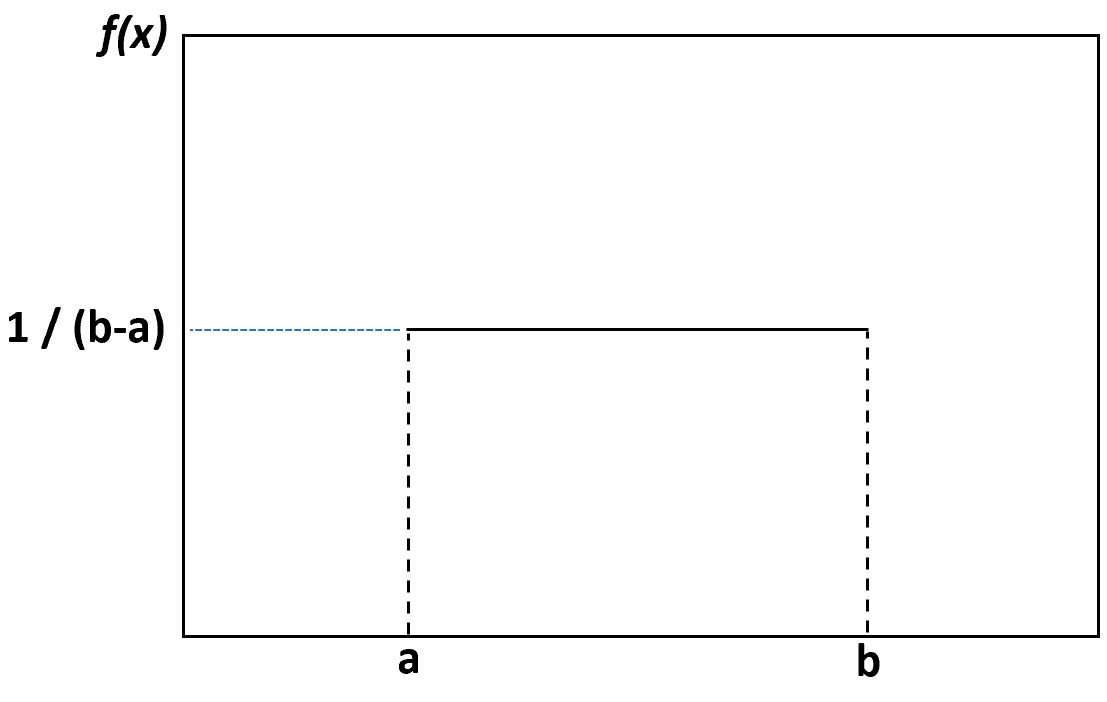
ทุกค่าระหว่างขีดจำกัดล่าง a และขีดจำกัดบน b มีความน่าจะเป็นที่จะเกิดขึ้นเท่ากัน และค่าใดๆ ที่อยู่นอกขีดจำกัดเหล่านี้มีความน่าจะเป็นเป็นศูนย์

ตัวอย่างเช่น ในตัวอย่างก่อนหน้านี้ เราบอกว่าน้ำหนักของโลมาจะกระจายเท่ากันระหว่าง 100 ถึง 150 ปอนด์ ต่อไปนี้เป็นวิธีแสดงภาพการกระจายนี้:

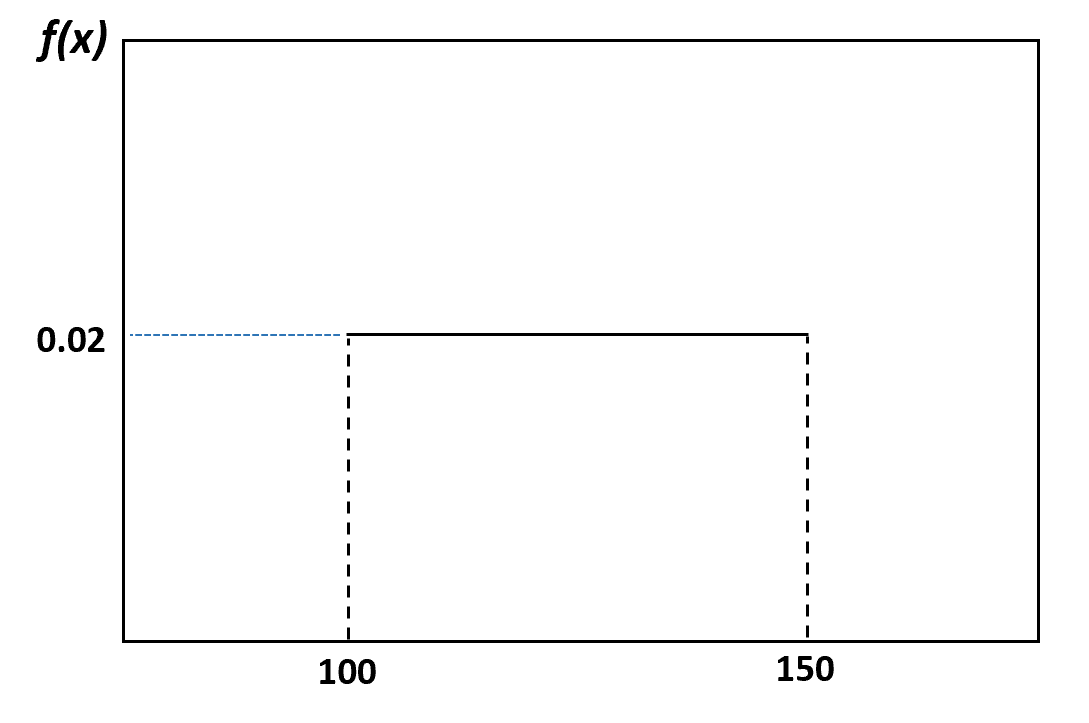
และความน่าจะเป็นที่โลมาสุ่มเลือกมาจะมีน้ำหนักระหว่าง 120 ถึง 130 ปอนด์ สามารถมองเห็นได้ดังนี้

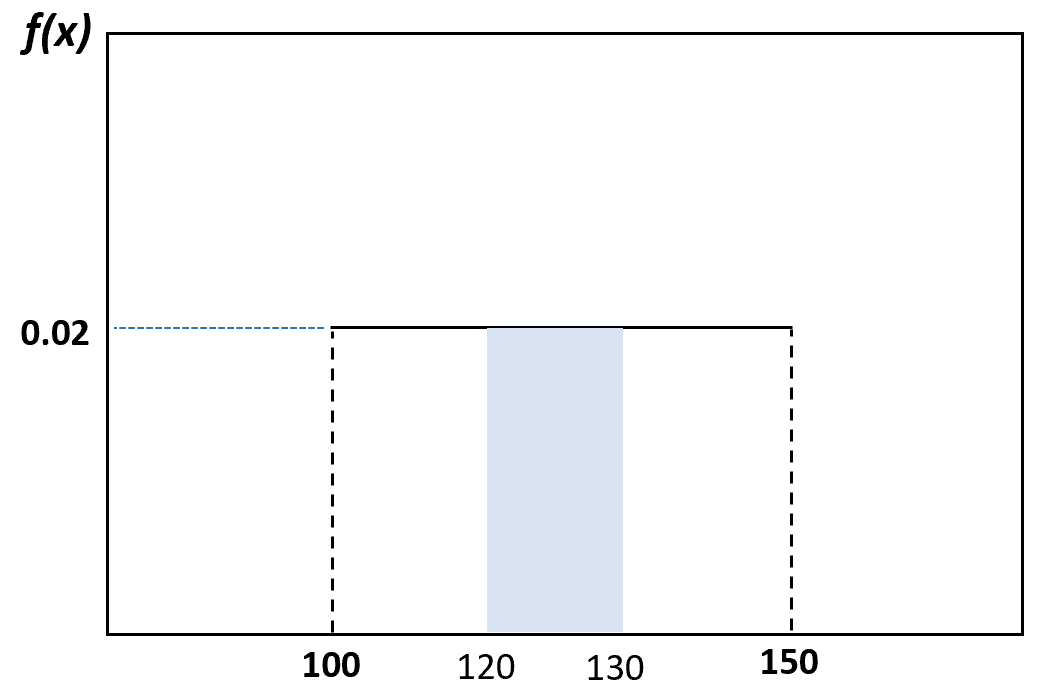
คุณสมบัติของการกระจายแบบสม่ำเสมอ

การกระจายแบบสม่ำเสมอมีคุณสมบัติดังต่อไปนี้:

• เฉลี่ย: (ก + ข) / 2
• ค่ามัธยฐาน: (a + b) / 2
• ส่วนเบี่ยงเบนมาตรฐาน: √ (ข – ก) ² / 12
• ความแตกต่าง: (ข – ก) ^2/12

ตัวอย่างเช่น สมมติว่าน้ำหนักของโลมามีการกระจายเท่าๆ กันระหว่าง 100 ถึง 150 ปอนด์

เราสามารถคำนวณคุณสมบัติต่อไปนี้สำหรับการแจกแจงนี้:

• น้ำหนักเฉลี่ย: (a + b) / 2 = (150 + 100) / 2 = 125
• น้ำหนักเฉลี่ย: (a + b) / 2 = (150 + 100) / 2 = 125
• ค่าเบี่ยงเบนมาตรฐานของน้ำหนัก: √ (150 – 100) ² / 12 = 14.43
• การเปลี่ยนแปลงน้ำหนัก: (150 – 100) ² / 12 = 208.33

ปัญหาเกี่ยวกับแนวทางปฏิบัติในการจัดจำหน่ายที่สม่ำเสมอ

ใช้แบบฝึกหัดแก้ปัญหาต่อไปนี้เพื่อทดสอบความรู้ของคุณเกี่ยวกับการกระจายตัวแบบสม่ำเสมอ

คำถามที่ 1: มีรถบัสมาจอดที่ป้ายรถเมล์ทุกๆ 20 นาที ถ้ามาถึงป้ายรถเมล์ ความน่าจะเป็นที่รถเมล์จะมาถึงภายใน 8 นาทีหรือน้อยกว่านั้นคือเท่าไร?

โซลูชันที่ 1: เวลารอขั้นต่ำคือ 0 นาที และเวลารอสูงสุดคือ 20 นาที ดอกเบี้ยล่างคือ 0 นาที และดอกเบี้ยบนคือ 8 นาที

ดังนั้น เราจะคำนวณความน่าจะเป็นดังนี้:

ป(0 < X < 8) = (8-0) / (20-0) = 8/20 = 0.4 .

คำถามที่ 2: ระยะเวลาของเกม NBA จะกระจายเท่ากันระหว่าง 120 ถึง 170 นาที ความน่าจะเป็นที่เกม NBA ที่เลือกแบบสุ่มจะใช้เวลานานกว่า 155 นาทีเป็นเท่าใด

โซลูชันที่ 2: ระยะเวลาขั้นต่ำคือ 120 นาที และระยะเวลาสูงสุดคือ 170 นาที ดอกเบี้ยล่างคือ 155 นาที และดอกเบี้ยบนคือ 170 นาที

ดังนั้น เราจะคำนวณความน่าจะเป็นดังนี้:

ป(155 < X < 170) = (170-155) / (170-120) = 15/50 = 0.3 .

คำถามที่ 3: น้ำหนักของกบบางสายพันธุ์จะกระจายเท่ากันระหว่าง 15 ถึง 25 กรัม ถ้าคุณเลือกกบโดยการสุ่ม ความน่าจะเป็นที่กบจะมีน้ำหนักระหว่าง 17 ถึง 19 กรัม เป็นเท่าใด

แนวทางที่ 3: น้ำหนักขั้นต่ำคือ 15 กรัม และน้ำหนักสูงสุดคือ 25 กรัม ดอกเบี้ยล่าง 17 กรัม และดอกเบี้ยบน 19 กรัม

ดังนั้น เราจะคำนวณความน่าจะเป็นดังนี้:

ป(17 < X < 19) = (19-17) / (25-15) = 2/10 = 0.2 .

หมายเหตุ: เราสามารถใช้เครื่องคำนวณการแจกแจงแบบสม่ำเสมอเพื่อตรวจสอบคำตอบของปัญหาแต่ละข้อเหล่านี้