การกระจายไคสแควร์

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 4, 2023 ความน่าจะเป็น 0 ความคิดเห็น

บทความนี้จะอธิบายว่าการกระจายตัวแบบไคสแควร์คืออะไร และใช้เพื่ออะไร นอกจากนี้ คุณจะพบกราฟการกระจายไคสแควร์และคุณสมบัติของกราฟนั้น

การกระจายไคสแควร์คืออะไร?

การแจกแจงแบบไคสแควร์ เป็นการแจกแจงความน่าจะเป็นซึ่งมีสัญลักษณ์เป็น χ² แม่นยำยิ่งขึ้น การแจกแจงแบบไคสแควร์คือผลรวมของกำลังสองของตัวแปรสุ่มอิสระ k ที่มีการแจกแจงแบบปกติ

ดังนั้น การแจกแจงแบบไคสแควร์จึงมีดีกรีอิสระเป็น k ดังนั้น การแจกแจงแบบไคสแควร์จึงมีดีกรีอิสระมากเท่ากับผลรวมของกำลังสองของตัวแปรที่แจกแจงตามปกติที่มันเป็นตัวแทน

$\displaystyle X\sim\chi^2_k \ \color{orange}\bm{\longrightarrow}\color{black}\ \begin{array}{l}\text{Distribuci\'on chi-cuadrado}\\[2ex]\text{con k grados de libertad}\end{array}$

การแจกแจงแบบไคสแควร์เรียกอีกอย่างว่า การแจกแจงแบบเพียร์สัน

ควรสังเกตว่าการแจกแจงไคสแควร์เป็นกรณีพิเศษของการแจกแจงแกมมา

การแจกแจงแบบไคสแควร์ใช้กันอย่างแพร่หลายในการอนุมานทางสถิติ เช่น ในการทดสอบสมมติฐานและช่วงความเชื่อมั่น เราจะดูด้านล่างว่าการใช้งานของการแจกแจงความน่าจะเป็นประเภทนี้มีอะไรบ้าง

กราฟการกระจายไคสแควร์

เมื่อเราเห็นคำจำกัดความของการแจกแจงแบบไคสแควร์ เราจะเห็นตัวอย่างต่างๆ ของการแจกแจงประเภทนี้ที่แสดงเป็นภาพกราฟิก ด้านล่างนี้คุณจะเห็นได้ว่าแผนภาพความน่าจะเป็นของการแจกแจงแบบไคสแควร์เปลี่ยนแปลงไปอย่างไร ขึ้นอยู่กับระดับความเป็นอิสระ

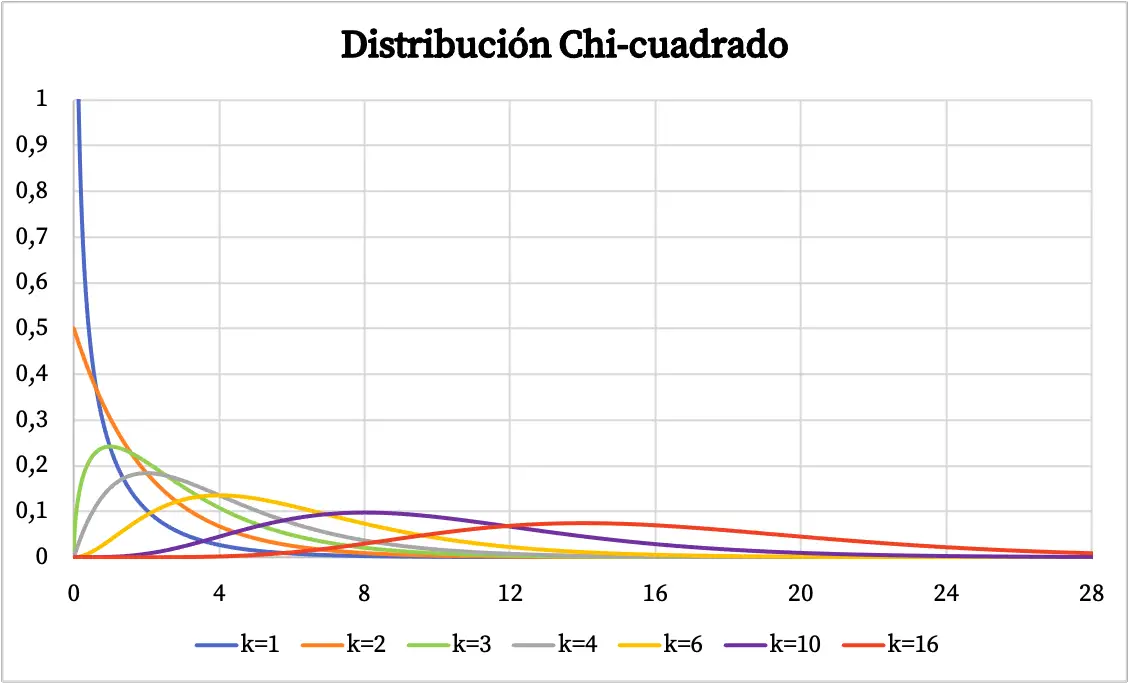
ฟังก์ชันความหนาแน่นของการแจกแจงแบบไคสแควร์ได้แสดงไว้ในกราฟด้านบน ในทางกลับกัน กราฟของฟังก์ชันการแจกแจงความน่าจะเป็นสะสมแบบไคสแควร์จะเป็นดังนี้:

➤ ดู: ตารางการแจกแจงไคสแควร์

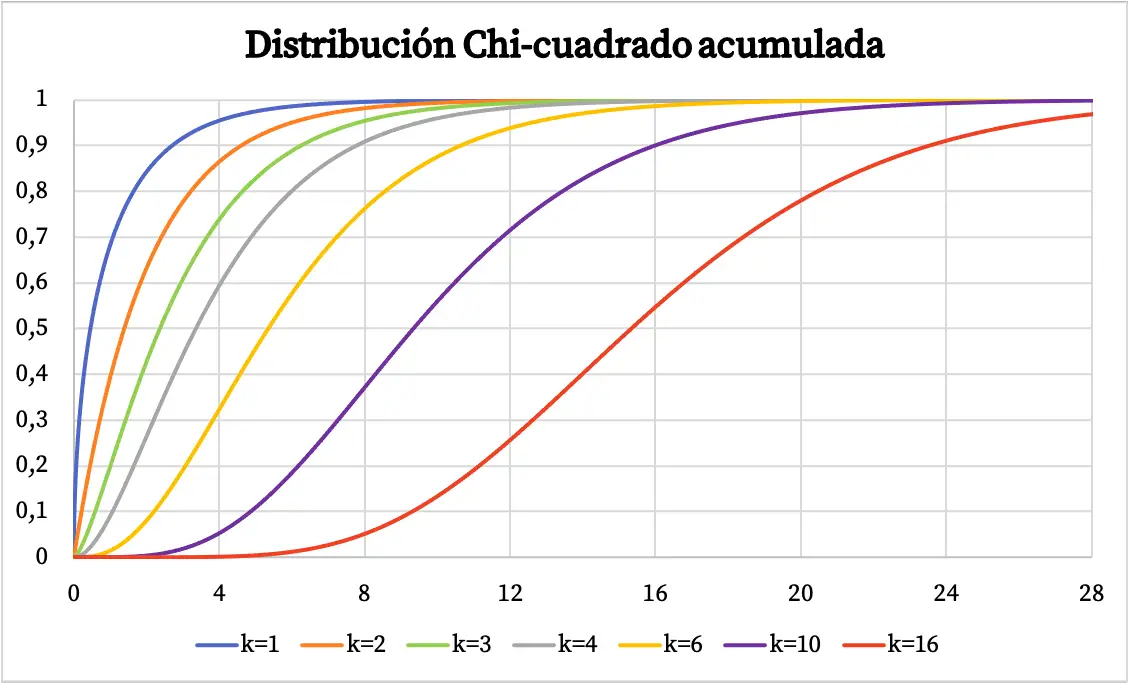
ลักษณะเฉพาะของการแจกแจงแบบไคสแควร์

ในส่วนนี้ เราจะดูคุณสมบัติที่สำคัญที่สุดของการแจกแจงไคสแควร์ที่เกี่ยวข้องกับทฤษฎีและสถิติความน่าจะเป็น

ค่าเฉลี่ยของการแจกแจงแบบไคสแควร์เท่ากับระดับความอิสระของมัน

$\begin{array}{c}X\sim\chi^2_k\\[2ex] E[X]=k\end{array}$

ความแปรปรวนของการแจกแจงแบบไคสแควร์เท่ากับสองเท่าของระดับความเป็นอิสระของการแจกแจง

$\begin{array}{c}X\sim\chi^2_k\\[2ex] Var(X)=2\cdot k\end{array}$

รูปแบบของการแจกแจงแบบไคสแควร์จะน้อยกว่าระดับความอิสระ 2 หน่วย ตราบใดที่การแจกแจงมีระดับความอิสระมากกว่าหนึ่งระดับ

$Mo=k-2 \qquad \text{si } k\geq 2$

ฟังก์ชันความหนาแน่นของการแจกแจงแบบไคสแควร์จะเป็นศูนย์ถ้า x=0 อย่างไรก็ตาม สำหรับค่า x ที่มากกว่า 0 ฟังก์ชันความหนาแน่นของการแจกแจงแบบไคสแควร์ถูกกำหนดโดยสูตรต่อไปนี้:

$\displaystyle P[X=x]= \frac{(1/2)^{k/2}}{\Gamma(k/2)} x^{k/2 - 1} e^{-x/2}$

ฟังก์ชันการแจกแจงสะสมของการแจกแจงแบบไคสแควร์อยู่ภายใต้สูตรต่อไปนี้:

$\displaystyle P[X\leq x]=\frac{\gamma(k/2,x/2)}{\Gamma(k/2)}$

ค่าสัมประสิทธิ์ความเบ้ของการแจกแจงแบบไคสแควร์คือรากที่สองของผลหารของ 8 หารด้วยจำนวนองศาอิสระของการแจกแจง

$\displaystyle A=\sqrt{\frac{8}{k}}$

ความโด่งของการแจกแจงไคสแควร์คำนวณโดยใช้นิพจน์ต่อไปนี้:

$C=3+\cfrac{12}{k}$

เนื่องจากทฤษฎีบทขีดจำกัดจุดศูนย์กลาง การแจกแจงแบบไคสแควร์สามารถประมาณได้โดยการแจกแจงแบบปกติหาก k มีค่ามากพอ

$\displaystyle\lim_{k \to \infty} \frac{\chi^2_k (x)}{ k } = N_{\left(1,\sqrt{2/k}\right)} (x)$

การประยุกต์การกระจายตัวแบบไคสแควร์

การแจกแจงแบบไคสแควร์มีการนำไปใช้งานทางสถิติได้หลากหลาย ในความเป็นจริง ยังมีการทดสอบไคสแควร์ซึ่งใช้ในการตรวจสอบความเป็นอิสระระหว่างตัวแปรและความเหมาะสมของการแจกแจงทางทฤษฎี ตัวอย่างเช่น การทดสอบไคสแควร์สามารถใช้เพื่อระบุได้ว่าข้อมูลของกลุ่มตัวอย่างสอดคล้องกับการแจกแจงแบบปัวซงหรือไม่

ในการวิเคราะห์การถดถอยเชิงเส้น การแจกแจงแบบไคสแควร์ยังใช้ในการประมาณค่าเฉลี่ยของประชากรที่แจกแจงแบบปกติ และเพื่อประมาณความชันของเส้นศึกษาการถดถอยเชิงเส้น

สุดท้ายนี้ การแจกแจงแบบ Chi Square ยังมีส่วนร่วมในการวิเคราะห์ความแปรปรวน ผ่านความสัมพันธ์กับการแจกแจงแบบ Snedecor F

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม