การสุ่มตัวอย่างการกระจายตัวของผลต่างของค่าเฉลี่ย

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 3, 2023 สถิติ 0 ความคิดเห็น

บทความนี้จะอธิบายว่าการกระจายตัวอย่างสำหรับความแตกต่างระหว่างสองค่าเฉลี่ยในสถิติคืออะไร นอกจากนี้คุณยังจะพบสูตรสำหรับการกระจายตัวอย่างความแตกต่างของค่าเฉลี่ยและแบบฝึกหัดแก้ไขทีละขั้นตอนอีกด้วย

การกระจายตัวอย่างความแตกต่างของค่าเฉลี่ยคืออะไร?

การกระจายตัวตัวอย่างของความแตกต่างในค่าเฉลี่ย คือการกระจายที่เป็นผลจากการคำนวณความแตกต่างระหว่างค่าเฉลี่ยของกลุ่มตัวอย่างที่เป็นไปได้ทั้งหมดจากประชากรสองกลุ่มที่แตกต่างกัน

กล่าวคือ เพื่อให้ได้การกระจายตัวตัวอย่างของความแตกต่างในค่าเฉลี่ย จะต้องเลือกตัวอย่างที่เป็นไปได้ทั้งหมดจากประชากรที่ทำการศึกษา 2 กลุ่ม จากนั้นจึงคำนวณค่าเฉลี่ยของแต่ละตัวอย่างที่เลือก และสุดท้ายคือความแตกต่างระหว่างค่าเฉลี่ยทั้งหมดที่คำนวณจากประชากรทั้งสอง ดังนั้นชุดของค่าที่ได้รับหลังจากการประยุกต์ใช้การดำเนินการทั้งหมดเหล่านี้ทำให้เกิดการกระจายตัวอย่างความแตกต่างของค่าเฉลี่ย

การสุ่มตัวอย่างการกระจายตัวของผลต่างของค่าเฉลี่ย

ความแตกต่างของค่าเฉลี่ยการกระจายตัวอย่างใช้ในการคำนวณความน่าจะเป็นที่ความแตกต่างระหว่างสอง ค่าเฉลี่ยของกลุ่มตัวอย่างที่เลือกแบบสุ่ม จากสองประชากรที่แตกต่างกันนั้นใกล้เคียงกับความแตกต่างในค่าเฉลี่ยประชากร

➤ ดู: การกระจายตัวอย่างค่าเฉลี่ย

สูตรการกระจายตัวอย่างค่าผลต่างของค่าเฉลี่ย

หากขนาดของกลุ่มตัวอย่างมีขนาดใหญ่เพียงพอ (n ₁ ≥30 และ n ₂ ≥30) การกระจายตัวของค่าความแตกต่างในค่าเฉลี่ยจะเป็นไปตามการกระจายตัวแบบปกติ แม่นยำยิ่งขึ้นพารามิเตอร์ของการแจกแจงดังกล่าวจะถูกคำนวณดังนี้:

$\begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}$

หมายเหตุ: หากประชากรทั้งสองเป็นการ แจกแจงแบบปกติ การกระจายตัวอย่างของความแตกต่างในค่าเฉลี่ยจะเป็นไปตามการแจกแจงแบบปกติโดยไม่คำนึงถึงขนาดตัวอย่าง

ดังนั้น เนื่องจากการกระจายตัวตัวอย่างของความแตกต่างในค่าเฉลี่ยถูกกำหนดโดยการแจกแจงแบบปกติ สูตรในการคำนวณสถิติของการกระจายตัวอย่างของความแตกต่าง ในค่าเฉลี่ยจึงเป็นดังนี้

$Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

ทอง:

$\overline{x_i}$

คือค่าเฉลี่ยของกลุ่มตัวอย่าง i
$\mu_i$

คือค่าเฉลี่ยของประชากร i
$\sigma_i$

คือค่าเบี่ยงเบนมาตรฐานของประชากร i
$n_i$

คือขนาดตัวอย่าง i
$Z$

เป็นตัวแปรที่กำหนดโดยการแจกแจงแบบปกติมาตรฐาน N(0,1)

โปรดทราบว่าตัวอย่างจากประชากรที่แตกต่างกันอาจมีขนาดตัวอย่างที่แตกต่างกัน

ตัวอย่างที่เป็นรูปธรรมของการกระจายตัวอย่างความแตกต่างของค่าเฉลี่ย

เมื่อเราเห็นคำจำกัดความของความแตกต่างของค่าเฉลี่ยการกระจายตัวอย่างและสูตรของมัน เราจะดูตัวอย่างทีละขั้นตอนเพื่อทำความเข้าใจแนวคิดเรื่องความแตกต่างของการกระจายตัวอย่างเฉลี่ย

ในการศึกษาทางสถิติ เราต้องการวิเคราะห์ความแตกต่างระหว่างความสูงของเด็กผู้ชายและเด็กผู้หญิงในช่วงอายุหนึ่งๆ เรารู้ว่าการกระจายตัวที่กำหนดประชากรเด็กผู้ชายวัยนี้มีค่าเฉลี่ย 157 เซนติเมตร และค่าเบี่ยงเบนมาตรฐาน 9 เซนติเมตร ในทางกลับกัน การกระจายตัวที่กำหนดประชากรเด็กผู้หญิงวัยนี้มีค่าเฉลี่ย 148 ซม. และส่วนเบี่ยงเบนมาตรฐาน 7 ซม. ถ้าเลือกกลุ่มตัวอย่างเด็กผู้ชายในวัยนี้ 30 คน และเด็กผู้หญิงในวัยนี้ 35 คน ความน่าจะเป็นที่ความสูงเฉลี่ยของกลุ่มตัวอย่างเด็กผู้ชายจะมากกว่าความสูงเฉลี่ยของกลุ่มตัวอย่างเด็กผู้หญิง 12 ซม. เป็นเท่าใด

ในการแก้ปัญหานี้ สิ่งแรกที่ต้องทำคือการคำนวณสถิติของผลต่างของการกระจายตัวตัวอย่างเฉลี่ย ดังนั้นเราจึงใช้สูตรที่เห็นด้านบน:

$Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right)}=\cfrac{12-(157-148)}{\displaystyle\sqrt{\frac{9^2}{30}+\frac{7^2}{35}}}=1,48$

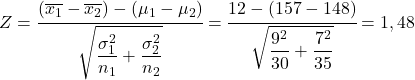
ดังนั้น ความน่าจะเป็นที่ส่วนสูงตัวอย่างโดยเฉลี่ยของเด็กผู้ชายจะมากกว่าส่วนสูงเฉลี่ยของเด็กผู้หญิง 12 ซม. จึงเท่ากับความน่าจะเป็นที่ตัวแปร Z มากกว่า 1.48

$P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”253″ style=”vertical-align: -5px;”></p> </p> <p> ดังนั้นเราจึงมองหาความน่าจะเป็นของ Z>1.48 ใน <a href=$ ตารางของ Z :

$P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]=0,0694″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”331″ style=”vertical-align: -5px;”></p> </p> <p> กล่าวโดยสรุป ความน่าจะเป็นที่ส่วนสูงตัวอย่างโดยเฉลี่ยของเด็กผู้ชายจะสูงกว่าส่วนสูงเฉลี่ยของเด็กผู้หญิง 12 ซม. คือ 6.94%</p> </div>  <div class=$

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม

การกระจายตัวอย่างความแตกต่างของค่าเฉลี่ยคืออะไร?

สูตรการกระจายตัวอย่างค่าผลต่างของค่าเฉลี่ย

ตัวอย่างที่เป็นรูปธรรมของการกระจายตัวอย่างความแตกต่างของค่าเฉลี่ย

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

เพิ่มความคิดเห็น