การกระจายตัวอย่างค่าเฉลี่ย

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 3, 2023 สถิติ 0 ความคิดเห็น

บทความนี้จะอธิบายว่าการกระจายตัวตัวอย่างของค่าเฉลี่ยในสถิติเป็นอย่างไร นอกจากนี้คุณยังจะพบสูตรการกระจายตัวอย่างเฉลี่ยและแบบฝึกหัดแก้ไขทีละขั้นตอน

การกระจายตัวตัวอย่างของค่าเฉลี่ยคืออะไร?

การกระจายตัวอย่างค่าเฉลี่ย (หรือ การกระจายตัวอย่างเฉลี่ย ) คือการแจกแจงที่เป็นผลจากการคำนวณค่าเฉลี่ยตัวอย่างของแต่ละตัวอย่างที่เป็นไปได้จากประชากร นั่นคือ ชุดของ ค่าเฉลี่ยตัวอย่าง จากตัวอย่างที่เป็นไปได้ทั้งหมดจากประชากรจะก่อให้เกิดการกระจายตัวของค่าเฉลี่ยตัวอย่าง

หรืออีกนัยหนึ่ง ถ้าเราศึกษาตัวอย่างทั้งหมดที่สามารถนำมาจากประชากรและคำนวณค่าเฉลี่ยของแต่ละตัวอย่าง ชุดของค่าที่คำนวณได้จะสร้างการกระจายตัวตัวอย่างของค่าเฉลี่ยตัวอย่าง

ในสถิติ การกระจายตัวตัวอย่างของค่าเฉลี่ยใช้ในการคำนวณความน่าจะเป็นที่จะเข้าใกล้ค่าของค่าเฉลี่ยประชากร เมื่อวิเคราะห์ตัวอย่างเดียว

สูตรการกระจายตัวอย่างค่าเฉลี่ย

เมื่อพิจารณาจากประชากรที่เป็นไปตาม การแจกแจงความน่าจะเป็นแบบปกติ ด้วยค่าเฉลี่ย

$\mu$

และค่าเบี่ยงเบนมาตรฐาน

$\sigma$

และดึงตัวอย่างขนาดออกมา

$n$

การกระจายตัวตัวอย่างของค่าเฉลี่ยจะถูกกำหนดโดยการแจกแจงแบบปกติที่มีลักษณะดังต่อไปนี้:

$\begin{array}{c}\mu_{\overline{x}}=\mu \qquad \sigma_{\overline{x}}=\cfrac{\sigma}{\sqrt{n}}\\[4ex]\displaystyle N_{\overline{x}}\left(\mu, \frac{\sigma}{\sqrt{n}}\right) \end{array}$

ทอง

$\mu_{\overline{x}}$

คือค่าเฉลี่ยของการกระจายตัวตัวอย่างของค่าเฉลี่ยและ

$\sigma_{\overline{x}}$

คือค่าเบี่ยงเบนมาตรฐาน นอกจากนี้,

$\cfrac{\sigma}{\sqrt{n}}$

คือค่าคลาดเคลื่อนมาตรฐานของการกระจายตัวตัวอย่าง

หมายเหตุ: หากประชากรไม่เป็นไปตามการแจกแจงแบบปกติแต่ขนาดของกลุ่มตัวอย่างมีขนาดใหญ่ (n>30) การกระจายตัวตัวอย่างของค่าเฉลี่ยสามารถประมาณได้กับการแจกแจงแบบปกติครั้งก่อนโดยใช้ทฤษฎีบทขีดจำกัดศูนย์กลาง

ดังนั้น เนื่องจากการกระจายตัวตัวอย่างของค่าเฉลี่ยเป็นไปตามการแจกแจงแบบปกติ สูตรในการคำนวณความน่าจะเป็นใดๆ ที่เกี่ยวข้องกับค่าเฉลี่ยตัวอย่าง จึงเป็นดังนี้:

$Z=\cfrac{\overline{x}-\mu}{\displaystyle\frac{\sigma}{\sqrt{n}}}$

ทอง:

$\overline{x}$

คือค่าเฉลี่ยตัวอย่าง
$\mu$

นี่คือค่าเฉลี่ยประชากร
$s$

คือค่าเบี่ยงเบนมาตรฐานประชากร
$n$

คือขนาดตัวอย่าง
$Z$

เป็นตัวแปรที่กำหนดโดยการแจกแจงแบบปกติมาตรฐาน N(0,1)

ตัวอย่างจริงของการกระจายตัวอย่างค่าเฉลี่ย

หลังจากเห็นคำจำกัดความของการแจกแจงตัวอย่างของค่าเฉลี่ยและสูตรที่เกี่ยวข้องแล้ว เรามาแก้ตัวอย่างเพื่อทำความเข้าใจแนวคิดกันดีกว่า

น้ำหนักของนักศึกษามหาวิทยาลัยเป็นไปตามการแจกแจงแบบปกติโดยมีค่าเฉลี่ย 68 กิโลกรัม และส่วนเบี่ยงเบนมาตรฐาน 9 กิโลกรัม มุ่งมั่น:
1. ความน่าจะเป็นที่ค่าเฉลี่ยของกลุ่มตัวอย่างสุ่มของนักเรียน 25 คน น้อยกว่า 66 กิโลกรัม เป็นเท่าใด
2. ถ้าเก็บตัวอย่าง 300 ตัวอย่าง โดยมีขนาดนักเรียน 25 คนต่อคน ค่าเฉลี่ยตัวอย่างจะมีน้ำหนักน้อยกว่า 66 กิโลกรัมจำนวนเท่าใด

ก่อนอื่น เราต้องคำนวณค่าของสถิติที่เกี่ยวข้อง โดยใช้สูตรที่เราเห็นด้านบน:

$\displaystyle Z=\frac{\overline{x}-\mu}{\displaystyle\frac{\sigma}{\sqrt{n}}}=\frac{66-68}{\displaystyle\frac{9}{\sqrt{25}}}=-1,11$

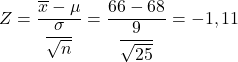
ความน่าจะเป็นที่เรากำลังมองหาจึงสอดคล้องกับค่า Z=-1.11 ของส่วนท้ายด้านซ้ายของการแจกแจงแบบปกติมาตรฐาน ซึ่งสามารถหาได้ง่ายจากตารางความน่าจะเป็นของ Z ดังนั้นเราจึงใช้ตาราง Z เพื่อกำหนดความน่าจะเป็นที่ปัญหาถามเรา:

$P[\overline{x}\leq 66]=P[Z\leq -1,11] =0,1335$

➤ ดูที่: ตาราง Z

ตอนนี้เรารู้ความน่าจะเป็นที่ค่าเฉลี่ยของกลุ่มตัวอย่างสุ่มน้อยกว่า 66 กิโลกรัม หากต้องการทราบจำนวนตัวอย่างหมายถึงน้อยกว่า 66 กิโลกรัม โดยเลือกตัวอย่าง 300 ตัวอย่างเท่ากัน เราจำเป็นต้องคูณความน่าจะเป็นที่คำนวณได้ด้วยจำนวนตัวอย่างทั้งหมดที่นำมา:

$0,1335\cdot 300 =40,05 \approx 40$

ดังนั้นตัวอย่างที่สกัดได้ประมาณ 40 ตัวอย่างจะมีค่าเฉลี่ยน้อยกว่า 66 กิโลกรัม

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม

การกระจายตัวตัวอย่างของค่าเฉลี่ยคืออะไร?

สูตรการกระจายตัวอย่างค่าเฉลี่ย

ตัวอย่างจริงของการกระจายตัวอย่างค่าเฉลี่ย

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

เพิ่มความคิดเห็น