การกระจายตัวอย่างความแตกต่างในสัดส่วน

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 3, 2023 สถิติ 0 ความคิดเห็น

บทความนี้จะอธิบายว่าการกระจายตัวอย่างตามสัดส่วนแตกต่างกันอย่างไร และใช้เพื่ออะไรในสถิติ นอกจากนี้ยังมีการนำเสนอความแตกต่างในสูตรการกระจายตัวอย่างตามสัดส่วนและแบบฝึกหัดแก้ไขทีละขั้นตอนด้วย

การกระจายตัวอย่างความแตกต่างในสัดส่วนคืออะไร?

ความแตกต่างในสัดส่วนการกระจายตัวอย่าง คือการกระจายที่เป็นผลจากการคำนวณความแตกต่างระหว่างสัดส่วนตัวอย่างของตัวอย่างที่เป็นไปได้ทั้งหมดจากประชากรสองกลุ่มที่แตกต่างกัน

นั่นคือ กระบวนการเพื่อให้ได้การกระจายตัวตัวอย่างของความแตกต่างในสัดส่วน ประการแรก เพื่อแยกตัวอย่างที่เป็นไปได้ทั้งหมดจากประชากรสองกลุ่มที่แตกต่างกัน ประการที่สอง เพื่อกำหนดสัดส่วนของแต่ละตัวอย่างที่แยกออกมา และสุดท้าย เพื่อกำหนดความแตกต่างระหว่างทั้งหมด สัดส่วนของความแตกต่างของสัดส่วน ประชากรสองคน เพื่อให้ชุดผลลัพธ์ที่ได้รับหลังจากดำเนินการเหล่านี้ทำให้เกิดการกระจายตัวอย่างความแตกต่างในสัดส่วน

ในสถิติ ความแตกต่างในการกระจายตัวอย่างตามสัดส่วนจะถูกนำมาใช้ในการคำนวณความน่าจะเป็นที่ความแตกต่างระหว่าง สัดส่วนตัวอย่าง ของตัวอย่างที่เลือกแบบสุ่ม 2 ตัวอย่างนั้นใกล้เคียงกับความแตกต่างในสัดส่วนประชากร

➤ ดู: การจัดสรรการสุ่มตัวอย่างตามสัดส่วน

สูตรการกระจายตัวอย่างส่วนต่างของสัดส่วน

ตัวอย่างที่เลือกสำหรับความแตกต่างในสัดส่วนของการกระจายตัวอย่างจะถูกกำหนดโดย การแจกแจงแบบทวินาม เนื่องจากในทางปฏิบัติ สัดส่วนคืออัตราส่วนของกรณีที่ประสบความสำเร็จต่อจำนวนการสังเกตทั้งหมด

อย่างไรก็ตาม เนื่องจากทฤษฎีบทขีดจำกัดกลาง การแจกแจงแบบทวินามจึงสามารถประมาณได้กับ การแจกแจงความน่าจะเป็นแบบปกติ ดังนั้นการกระจายตัวอย่างส่วนต่างในสัดส่วนสามารถประมาณได้กับการแจกแจงแบบปกติโดยมีลักษณะดังต่อไปนี้

$\begin{array}{c}\displaystyle\mu_{\widehat{p_1}-\widehat{p_2}}=p_1-p_2 \qquad \sigma_{\widehat{p_1}-\widehat{p_2}}=\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\\[6ex]\displaystyle N_{p}\left(p_1-p_2, \sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\right) \end{array}$

หมายเหตุ: การกระจายตัวตัวอย่างของความแตกต่างในสัดส่วนสามารถประมาณได้เฉพาะกับการแจกแจงแบบปกติเท่านั้น

$n_1\geq30$

$n_2\geq 30$

$n_1p_1\geq5$

$n_2p_2\geq5$

$n_1q_1\geq5$

และ

$n_2q_2\geq5$

ดังนั้น เนื่องจากการกระจายตัวตัวอย่างของส่วนต่างในสัดส่วนสามารถประมาณได้กับการแจกแจงแบบปกติ สูตรในการคำนวณสถิติของการกระจายตัวตัวอย่างของส่วนต่างในสัดส่วน จึงเป็นดังนี้

$Z=\cfrac{(\widehat{p_1}-\widehat{p_2})-(p_1-p_2)}{\displaystyle\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}}$

ทอง:

$\widehat{p_i}$

คือสัดส่วนตัวอย่าง i
$p_i$

คือสัดส่วนของประชากร i
$q_i$

คือความน่าจะเป็นที่จะเกิดความล้มเหลวของประชากร i

$q_i=1-p_i$

.
$n_i$

คือขนาดตัวอย่าง i
$Z$

เป็นตัวแปรที่กำหนดโดยการแจกแจงแบบปกติมาตรฐาน N(0,1)

สูตรนี้คล้ายกับสูตรทดสอบสมมติฐานเรื่องความแตกต่างในสัดส่วน

ตัวอย่างที่เป็นรูปธรรมของการกระจายตัวอย่างส่วนต่างของสัดส่วน

หลังจากดูคำจำกัดความของความแตกต่างของการกระจายตัวอย่างตามสัดส่วนและสูตรของมันแล้ว คุณสามารถดูตัวอย่างที่แก้ไขได้ทีละขั้นตอนด้านล่างเพื่อทำความเข้าใจแนวคิดให้เสร็จสิ้น

คุณต้องการวิเคราะห์ความแม่นยำของโรงงานผลิตสองแห่ง โดยโรงงานแห่งหนึ่งผลิตในลักษณะที่มีชิ้นส่วนที่ผลิตเพียง 5% เท่านั้นที่มีข้อบกพร่อง ในขณะที่เปอร์เซ็นต์ของชิ้นส่วนที่ชำรุดของโรงงานอื่นคือ 8% หากเราเก็บตัวอย่างชิ้นส่วนจากโรงงานแห่งแรกจำนวน 200 ชิ้น และตัวอย่างจากโรงงานแห่งที่สองอีกจำนวน 280 ชิ้น ความน่าจะเป็นที่เปอร์เซ็นต์ของเสียในโรงงานผลิตแห่งแรกจะมากกว่าเปอร์เซ็นต์ของเสียในโรงงานแห่งที่สองเป็นเท่าใด การผลิต?

เพื่อให้ทราบข้อมูลปัญหาทั้งหมดให้เสร็จสิ้น ขั้นแรกเราจะคำนวณสัดส่วนของชิ้นส่วนที่ผลิตอย่างดีของแต่ละโรงงาน:

$\begin{array}{c}q_1=1-p_1=1-0,05=0,95\\[2ex]q_2=1-p_2=1-0,08=0,92\end{array}$

หากอัตราของเสียในโรงงานแห่งแรกมากกว่าอัตราของเสียในโรงงานแห่งที่สอง นั่นหมายความว่าสมการต่อไปนี้จะเป็นจริง:

$\widehat{p_1}-\widehat{p_2}>0″ title=”Rendered by QuickLaTeX.com” height=”18″ width=”89″ style=”vertical-align: -4px;”> ดังนั้น เพื่อพิจารณาความน่าจะเป็นของการกระจายตัวอย่างสำหรับความแตกต่างในสัดส่วน เราจำเป็นต้องใช้สูตรที่อธิบายไว้ในส่วนด้านบน: <p class=$ $Z=\cfrac{(\widehat{p_1}-\widehat{p_2})-(p_1-p_2)}{\displaystyle\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}}=\cfrac{0-(0,05-0,08)}{\displaystyle\sqrt{\frac{0,05\cdot 0,95}{200}+\frac{0,08\cdot 0,92}{280}}}=1,34$

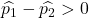
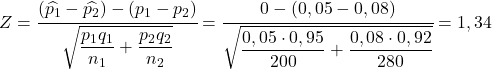
ดังนั้น ความน่าจะเป็นที่อัตราของเสียของโรงงานแห่งแรกมากกว่าอัตราของเสียของโรงงานแห่งที่สองจึงเท่ากับความน่าจะเป็นที่ตัวแปร Z มากกว่า 1.34:

$P[(\widehat{p_1}-\widehat{p_2})>0]=P[Z>1,34]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”242″ style=”vertical-align: -5px;”> สุดท้าย เราเพียงแค่ต้องค้นหาความน่าจะเป็นที่สอดคล้องกันใน <a href=$ ตารางการแจกแจงแบบปกติ และเราจะแก้ไขปัญหาได้แล้ว:

$P[(\widehat{p_1}-\widehat{p_2})>0]=P[Z>1,34]=0,0901″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”319″ style=”vertical-align: -5px;”> กล่าวโดยสรุป ความน่าจะเป็นที่สัดส่วนของเสียในโรงงานแห่งแรกจะมากกว่าสัดส่วนของเสียในโรงงานแห่งที่สองคือร้อยละ 9.01 <div style=$ ➤ ดู: การสุ่มตัวอย่างการกระจายตัวของผลต่างในค่าเฉลี่ย

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม

การกระจายตัวอย่างความแตกต่างในสัดส่วนคืออะไร?

สูตรการกระจายตัวอย่างส่วนต่างของสัดส่วน

ตัวอย่างที่เป็นรูปธรรมของการกระจายตัวอย่างส่วนต่างของสัดส่วน

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

เพิ่มความคิดเห็น