การกระจายตัวแบบปกติ

การแจกแจงแบบปกติ คือการแจกแจงความน่าจะเป็นที่พบบ่อยที่สุดในสถิติ

การแจกแจงแบบปกติมีลักษณะดังต่อไปนี้:

• รูปร่างระฆัง
• สมมาตร
• ค่าเฉลี่ยและค่ามัธยฐานเท่ากัน ทั้งสองแห่งตั้งอยู่ตรงกลางการกระจายสินค้า
• ข้อมูลประมาณ 68% อยู่ในช่วงเบี่ยงเบนมาตรฐานของค่าเฉลี่ย
• ข้อมูลประมาณ 95% อยู่ภายในค่าเบี่ยงเบนมาตรฐานสองค่าของค่าเฉลี่ย
• ข้อมูลประมาณ 99.7% อยู่ในค่าเบี่ยงเบนมาตรฐานสามค่าของค่าเฉลี่ย

สามแต้มสุดท้ายเรียกว่า กฎทั่วไป บางครั้งเรียกว่า กฎ 68-95-99.7

ที่เกี่ยวข้อง: Rule of Thumb (ประเด็นการปฏิบัติ)

วิธีการวาดเส้นโค้งปกติ

ในการวาดเส้นโค้งปกติ เราจำเป็นต้องทราบค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐาน

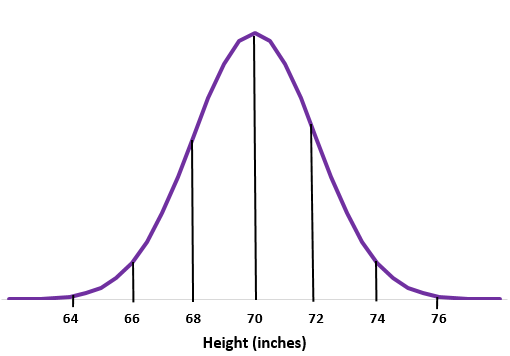
ตัวอย่างที่ 1: สมมติว่าความสูงของผู้ชายในโรงเรียนบางแห่งโดยปกติจะแจกแจงด้วยค่าเฉลี่ย $\mu =\; 70\; นิ้ว\; และ$ ค่าเบี่ยงเบนมาตรฐาน $\sigma \; =\; 2\; นิ้ว\; ร่างเส้นโค้งปกติ.$

ขั้นตอนที่ 1: ร่างเส้นโค้งปกติ

ขั้นตอนที่ 2: ค่าเฉลี่ย 70 นิ้วอยู่ตรงกลาง

ขั้นตอนที่ 3: แต่ละส่วนเบี่ยงเบนมาตรฐานสอดคล้องกับระยะทาง 2 นิ้ว

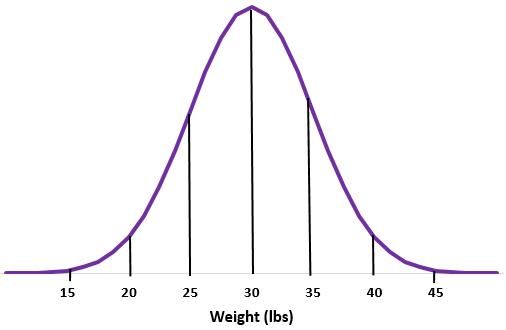
ตัวอย่างที่ 2: สมมติว่าน้ำหนักของนากบางสายพันธุ์ปกติจะกระจายโดยมีค่าเฉลี่ย $\mu =\; 30\; ปอนด์\; และ$ ค่าเบี่ยงเบนมาตรฐาน $\sigma \; =\; 5\; ปอนด์\; ร่างเส้นโค้งปกติ.$

ขั้นตอนที่ 1: ร่างเส้นโค้งปกติ

ขั้นตอนที่ 2: ค่าเฉลี่ย 30 ปอนด์อยู่ตรงกลาง

ขั้นตอนที่ 3: แต่ละส่วนเบี่ยงเบนมาตรฐานสอดคล้องกับระยะทาง 5 ปอนด์

วิธีค้นหาเปอร์เซ็นต์โดยใช้การแจกแจงแบบปกติ

กฎทั่วไป ซึ่งบางครั้งเรียกว่า กฎ 68-95-99.7 ระบุว่าสำหรับตัวแปรสุ่มแบบกระจายแบบปกติ 68% ของข้อมูลอยู่ในช่วงค่าเบี่ยงเบนมาตรฐานจากค่าเฉลี่ย 95% อยู่ในช่วงของสองมาตรฐาน ส่วนเบี่ยงเบนจากค่าเฉลี่ย และ 99.7% อยู่ภายในค่าเบี่ยงเบนมาตรฐานสามค่าจากค่าเฉลี่ย

การใช้กฎนี้เราสามารถตอบคำถามเกี่ยวกับเปอร์เซ็นต์ได้

ตัวอย่าง: สมมติว่าความสูงของผู้ชายในโรงเรียนบางแห่งโดยปกติจะแจกแจงด้วยค่าเฉลี่ย $\mu =\; 70\; นิ้ว\; และ$ ค่าเบี่ยงเบนมาตรฐาน $\sigma \; =\; 2\; นิ้ว$

$ผู้ชายในโรงเรียนนี้สูงเกิน\; 74\; นิ้วประมาณกี่เปอร์เซ็นต์$

สารละลาย:

ขั้นตอนที่ 1: ร่างการแจกแจงแบบปกติด้วยค่าเฉลี่ย $\mu =\; 70\; นิ้ว\; และ$ ค่าเบี่ยงเบนมาตรฐาน $\sigma \; =\; 2\; นิ้ว$

ขั้นตอนที่ 2: ความสูง 74 นิ้วคือค่าเบี่ยงเบนมาตรฐาน 2 ค่าที่สูงกว่าค่าเฉลี่ย เพิ่มเปอร์เซ็นต์ที่อยู่เหนือจุดนี้ลงในการแจกแจงแบบปกติ

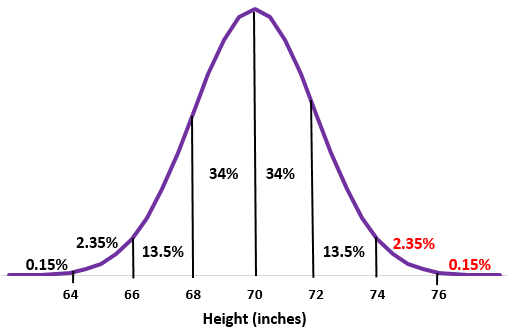
2.35% + 0.15% = 2.5%

ผู้ชายประมาณ 2.5% ในโรงเรียนนี้มีส่วนสูงเกิน 74 นิ้ว

$ผู้ชายในโรงเรียนนี้มีส่วนสูงระหว่าง\; 68\; นิ้วถึง\; 72\; นิ้วโดยประมาณกี่เปอร์เซ็นต์$

สารละลาย:

ขั้นตอนที่ 1: ร่างการแจกแจงแบบปกติด้วยค่าเฉลี่ย $\mu =\; 70\; นิ้ว\; และ$ ค่าเบี่ยงเบนมาตรฐาน $\sigma \; =\; 2\; นิ้ว$

ขั้นตอนที่ 2: ความสูง 68 นิ้วและ 72 นิ้วคือค่าเบี่ยงเบนมาตรฐานหนึ่งค่าที่ต่ำกว่าและสูงกว่าค่าเฉลี่ยตามลำดับ เพียงบวกเปอร์เซ็นต์ระหว่างสองจุดนี้ในการแจกแจงแบบปกติ

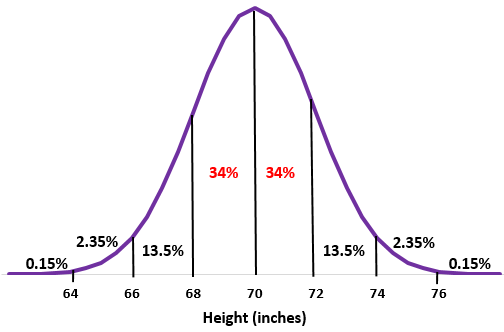
34% + 34% = 68%

ผู้ชายประมาณ 68% ในโรงเรียนนี้มีส่วนสูงระหว่าง 68 นิ้วถึง 72 นิ้ว

วิธีค้นหาจำนวนโดยใช้การแจกแจงแบบปกติ

นอกจากนี้เรายังสามารถใช้หลักทั่วไปเพื่อตอบคำถามเกี่ยวกับการนับได้

ตัวอย่าง: สมมติว่าน้ำหนักของนากบางสายพันธุ์ปกติจะกระจายโดยมีค่าเฉลี่ย $\mu =\; 30\; ปอนด์\; และ$ ค่าเบี่ยงเบนมาตรฐาน $\sigma \; =\; 5\; ปอนด์$

อาณานิคมบางแห่งมีนากเหล่านี้ 200 ตัว นากเหล่านี้มีน้ำหนักมากกว่า 35 ปอนด์ประมาณกี่ตัว?

สารละลาย:

ขั้นตอนที่ 1: ร่างการแจกแจงแบบปกติด้วยค่าเฉลี่ย $\mu =\; 30\; ปอนด์\; และ$ ค่าเบี่ยงเบนมาตรฐาน $\sigma \; =\; 5\; ปอนด์$

ขั้นตอนที่ 2: น้ำหนัก 35 ปอนด์คือค่าเบี่ยงเบนมาตรฐานหนึ่งค่าที่อยู่เหนือค่าเฉลี่ย เพิ่มเปอร์เซ็นต์ที่อยู่เหนือจุดนี้ลงในการแจกแจงแบบปกติ

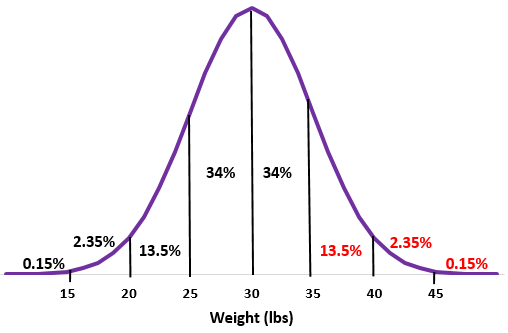
13.5% + 2.35% + 0.15% = 16%

ขั้นตอนที่ 3: เนื่องจากมีนาก 200 ตัวในอาณานิคม 16% ของ 200 = 0.16 * 200 = 32

ตัวนากประมาณ 32 ตัวในอาณานิคมนี้มีน้ำหนักมากกว่า 35 ปอนด์

มีนากประมาณกี่ตัวในอาณานิคมนี้ที่มีน้ำหนักน้อยกว่า 30 ปอนด์?

แทนที่จะทำตามขั้นตอนทั้งหมดที่เราเพิ่งทำไป เรารู้ได้ว่าค่ามัธยฐานของการแจกแจงแบบปกติเท่ากับค่าเฉลี่ย ซึ่งในกรณีนี้คือ 30 ปอนด์

ซึ่งหมายความว่านากครึ่งหนึ่งมีน้ำหนักมากกว่า 30 ปอนด์ และอีกครึ่งหนึ่งมีน้ำหนักน้อยกว่า 30 ปอนด์ ซึ่งหมายความว่า 50% ของตัวนาก 200 ตัวมีน้ำหนักน้อยกว่า 30 ปอนด์ ดังนั้น 0.5 * 200 = 100 ตัว

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้ให้ข้อมูลเพิ่มเติมเกี่ยวกับการแจกแจงแบบปกติ:

6 ตัวอย่างที่เป็นรูปธรรมของการแจกแจงแบบปกติ
การแจกแจงแบบปกติกับการแจกแจงแบบ t: ความแตกต่าง
วิธีการสร้างเส้นโค้งระฆังใน Excel
วิธีสร้าง Bell Curve ใน Python