การกระจายตัวอย่างตามสัดส่วน

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 3, 2023 สถิติ 0 ความคิดเห็น

บทความนี้จะอธิบายว่าการกระจายตัวอย่างตามสัดส่วนในสถิติคืออะไร ในทำนองเดียวกัน คุณจะพบสูตรการกระจายตัวอย่างตามสัดส่วนและแบบฝึกหัดแก้ไขทีละขั้นตอนอีกด้วย

การกระจายตัวอย่างตามสัดส่วนคืออะไร?

การกระจายตัวอย่างตามสัดส่วน (หรือ การกระจายตัวอย่างตามสัดส่วน ) คือการกระจายตัวที่เป็นผลมาจากการคำนวณสัดส่วนของแต่ละตัวอย่างที่เป็นไปได้จากประชากร นั่นคือ สัดส่วนการสุ่มตัวอย่าง ที่เป็นไปได้ทั้งหมดจากประชากรจากการกระจายตัวตัวอย่างของสัดส่วน

กล่าวอีกนัยหนึ่ง การกระจายตัวของสัดส่วนตัวอย่างได้มาจากการศึกษาตัวอย่างทั้งหมดที่สามารถเลือกได้จากประชากร และหาสัดส่วนการสุ่มตัวอย่างของแต่ละตัวอย่าง ดังนั้น ชุดของสัดส่วนตัวอย่างที่คำนวณได้จึงถือเป็นการกระจายตัวอย่างตามสัดส่วน

ในกรณีที่คุณสงสัยว่าการกระจายตัวของสัดส่วนตัวอย่างมีไว้เพื่ออะไร ในสถิติจะใช้เพื่อคำนวณความน่าจะเป็นที่จะเข้าใกล้ค่าของสัดส่วนประชากรเมื่อวิเคราะห์ตัวอย่างเดียว

➤ ดู: การกระจายตัวอย่างค่าเฉลี่ย

สูตรการกระจายตัวอย่างตามสัดส่วน

ที่จริงแล้ว เมื่อเราศึกษาสัดส่วนของกลุ่มตัวอย่าง เราจะวิเคราะห์กรณีความสำเร็จ ดังนั้น ตัวแปรสุ่มในการศึกษาจึงเป็นไปตาม การแจกแจงความน่าจะเป็นแบบทวินาม

ตามทฤษฎีบทขีดจำกัดกลาง สำหรับขนาดใหญ่ (n>30) เราสามารถทำให้การแจกแจงแบบทวินามเข้าใกล้การแจกแจงแบบปกติมากขึ้น ดังนั้น การกระจายตัวอย่างตามสัดส่วนจะใกล้เคียงกับการแจกแจงแบบปกติด้วยพารามิเตอร์ต่อไปนี้:

$\begin{array}{c}\displaystyle\mu_{p}=p \qquad \sigma_{p}=\sqrt{\frac{pq}{n}}\\[4ex]\displaystyle N_{p}\left(p, \sqrt{\frac{pq}{n}}\right) \end{array}$

ทอง

$p$

คือความน่าจะเป็นของความสำเร็จและ

$q$

คือความน่าจะเป็นที่จะล้มเหลว

$q=1-p$

หมายเหตุ: การแจกแจงแบบทวินามสามารถประมาณได้เฉพาะกับการแจกแจงแบบปกติเท่านั้น

$n>30″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”52″ style=”vertical-align: -2px;”> , <p class=$ $np\ge 5$

และ

$nq\ge 5$

➤ ดู: ตัวอย่างของการแจกแจงแบบปกติ

ดังนั้น เนื่องจากการกระจายตัวอย่างตามสัดส่วนสามารถประมาณได้กับการแจกแจงแบบปกติ สูตรในการคำนวณความน่าจะเป็นใดๆ ที่เกี่ยวข้องกับสัดส่วนของกลุ่มตัวอย่าง จึงเป็นดังนี้

$Z=\cfrac{\widehat{p}-p}{\displaystyle\sqrt{\frac{pq}{n}}}$

ทอง:

$\widehat{p}$

คือสัดส่วนตัวอย่าง
$p$

คือสัดส่วนของประชากร
$q$

คือความน่าจะเป็นที่จะล้มเหลวของประชากร

$q=1-p$

.
$n$

คือขนาดตัวอย่าง
$Z$

เป็นตัวแปรที่กำหนดโดยการแจกแจงแบบปกติมาตรฐาน N(0,1)

ตัวอย่างการกระจายตัวอย่างตามสัดส่วนที่เป็นรูปธรรม

เมื่อเราได้เห็นคำจำกัดความของการกระจายตัวอย่างตามสัดส่วนและสูตรที่เกี่ยวข้องแล้ว เราจะแสดงตัวอย่างที่แก้ไขทีละขั้นตอนด้านล่างเพื่อทำความเข้าใจแนวคิดนี้อย่างถ่องแท้

บริษัทอุตสาหกรรมแห่งหนึ่งซื้อชิ้นส่วนเป็นชุดจากโรงงานที่อ้างว่าผลิตชิ้นส่วนที่มีชิ้นส่วนชำรุดเพียง 3% เพื่อตรวจสอบสิ่งนี้ บริษัทจึงตัดสินใจวิเคราะห์คำสั่งซื้อชิ้นส่วนจำนวน 500 ชิ้น ความน่าจะเป็นที่จะพบชิ้นส่วนที่ชำรุดมากกว่า 5% ในตัวอย่างคือเท่าไร?

ในกรณีนี้ สัดส่วนของประชากรที่เราต้องการศึกษาคือ 0.03 ดังนั้นพารามิเตอร์ q จึงเท่ากับ 0.97

$\begin{array}{c}p=0,03\\[2ex]q=1-p=0,97\end{array}$

ดังนั้น เพื่อหาความน่าจะเป็นที่พวกเขาถามเรา เราต้องคำนวณสถิติที่เกี่ยวข้องโดยใช้สูตรที่เราเห็นในส่วนที่แล้ว:

$Z=\cfrac{\widehat{p}-p}{\displaystyle\sqrt{\frac{pq}{n}}}=\cfrac{0,05-0,03}{\displaystyle\sqrt{\frac{0,03\cdot 0,97}{500}}}=2,62$

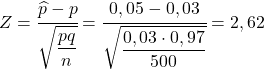
ดังนั้นความน่าจะเป็นที่จะได้ชิ้นส่วนที่ชำรุดมากกว่า 5% จึงเท่ากับความน่าจะเป็นดังต่อไปนี้:

$P\left[\widehat{p}>0,05\right]=P[Z>2,62]=1-P[Z\leq 2,62]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”360″ style=”vertical-align: -5px;”> สุดท้าย เรามองหาความน่าจะเป็นของ P[Z≤2.62] ใน <a href=$ ตารางการแจกแจง Z และคำนวณความน่าจะเป็นที่ปัญหาถามเรา:

$\begin{array}{l}P\left[\widehat{p}>0,05\right]=\\[2ex]=P[Z>2,62]=\\[2ex]=1-P[Z\leq 2,62]=\\[2ex]=1-0,9956=\\[2ex]=0,0044\end{array}” title=”Rendered by QuickLaTeX.com” height=”167″ width=”162″ style=”vertical-align: 0px;”> โดยสรุป ความน่าจะเป็นที่จะพบชิ้นส่วนที่มีข้อบกพร่องมากกว่า 5% ในตัวอย่างที่วิเคราะห์คือ 0.44% </div>  <div class=$

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม

การกระจายตัวอย่างตามสัดส่วนคืออะไร?

สูตรการกระจายตัวอย่างตามสัดส่วน

ตัวอย่างการกระจายตัวอย่างตามสัดส่วนที่เป็นรูปธรรม

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

เพิ่มความคิดเห็น