การกระจายเครื่องแบบไม่ต่อเนื่อง

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 3, 2023 ความน่าจะเป็น 0 ความคิดเห็น

บทความนี้จะอธิบายว่าการกระจายตัวแบบสม่ำเสมอแบบไม่ต่อเนื่องคืออะไร และสูตรเฉพาะของมันคืออะไร ในทำนองเดียวกัน คุณจะเห็นการแสดงแบบกราฟิกของการกระจายเครื่องแบบแบบแยกส่วนและคุณสมบัติของมัน

การกระจายเครื่องแบบแบบไม่ต่อเนื่องคืออะไร?

การแจกแจงแบบสม่ำเสมอแบบ ไม่ต่อเนื่องคือการแจกแจงความน่าจะเป็นแบบไม่ต่อเนื่อง โดยค่าทั้งหมดมีความน่าจะเป็นที่เท่ากัน กล่าวคือ ในการแจกแจงแบบสม่ำเสมอแบบไม่ต่อเนื่อง ค่าทั้งหมดมีความน่าจะเป็นที่จะเกิดขึ้นเท่ากัน

ตัวอย่างเช่น การทอยลูกเต๋าสามารถกำหนดได้ด้วยการกระจายแบบสม่ำเสมอแบบไม่ต่อเนื่อง เนื่องจากผลลัพธ์ที่เป็นไปได้ทั้งหมด (1, 2, 3, 4, 5 หรือ 6) มีความน่าจะเป็นที่จะเกิดขึ้นเท่ากัน

โดยทั่วไปการแจกแจงแบบสม่ำเสมอแบบไม่ต่อเนื่องจะมีพารามิเตอร์ลักษณะเฉพาะสองตัว คือ a และ b ซึ่งกำหนดช่วงของค่าที่เป็นไปได้ที่การแจกแจงสามารถทำได้ ดังนั้น เมื่อตัวแปรถูกกำหนดโดยการแจกแจงแบบแยกส่วน ตัวแปรนั้นจะถูกเขียนเป็น Uniform(a,b)

การแจกแจงแบบสม่ำเสมอแบบไม่ต่อเนื่องสามารถใช้เพื่ออธิบายการทดลองสุ่มได้ เพราะหากผลลัพธ์ทั้งหมดมีความน่าจะเป็นเท่ากัน แสดงว่าการทดลองนั้นเป็นแบบสุ่ม

สูตรการกระจายสม่ำเสมอแบบไม่ต่อเนื่อง

ตอนนี้เรารู้คำจำกัดความของการแจกแจงเครื่องแบบแบบไม่ต่อเนื่องแล้ว เราจะมาดูว่าสูตรอะไรที่ช่วยให้เราสามารถคำนวณความน่าจะเป็นที่จะปรากฏของค่าของการแจกแจงประเภทนี้

ฟังก์ชันความน่าจะเป็นของการแจกแจงแบบสม่ำเสมอแบบไม่ต่อเนื่องจะเป็นค่าคงที่ และค่าของมันจะเท่ากับ 1 ส่วนจำนวนผลลัพธ์ที่เป็นไปได้ทั้งหมด ดังนั้น สูตรสำหรับการกระจายสม่ำเสมอแบบไม่ต่อเนื่อง จึงเป็นดังนี้:

$P[X=x]=\cfrac{1}{n}=\cfrac{1}{b-a+1}$

ในทางกลับกัน สูตรสำหรับฟังก์ชันความน่าจะเป็นสะสมของการแจกแจงเครื่องแบบแบบไม่ต่อเนื่องมีดังนี้

$P[X\leq x]=\cfrac{\lfloor x \rfloor -a + 1}{b-a+1}$

ทอง

$a$

และ

$b$

เป็นพารามิเตอร์คุณลักษณะของการแจกแจงแบบสม่ำเสมอแบบไม่ต่อเนื่อง

แผนภาพการกระจายเครื่องแบบแบบไม่ต่อเนื่อง

เนื่องจากการแจกแจงแบบสม่ำเสมอแบบไม่ต่อเนื่องสามารถรับค่าบางค่าได้ในช่วงเวลาหนึ่งเท่านั้น การแสดงกราฟิกจึงประกอบด้วยจุด นอกจากนี้ ความน่าจะเป็นทั้งหมดจะเท่ากัน ดังนั้นทุกจุดในการแจกแจงแบบสม่ำเสมอแบบไม่ต่อเนื่องจึงมีพิกัดแนวตั้งที่เหมือนกัน

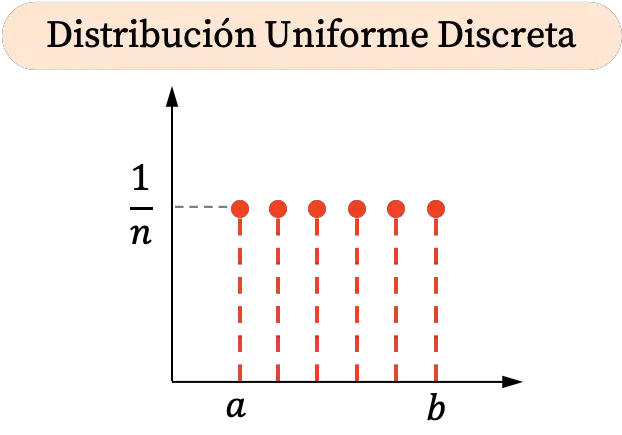
ในทางกลับกัน กราฟความน่าจะเป็นสะสมของการแจกแจงเครื่องแบบแบบไม่ต่อเนื่องจะเป็นดังนี้:

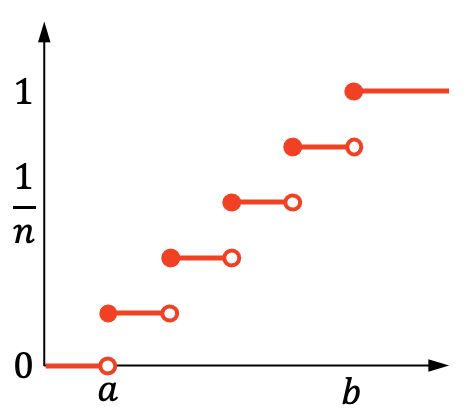
ลักษณะของการกระจายเครื่องแบบแบบไม่ต่อเนื่อง

การกระจายเครื่องแบบแบบไม่ต่อเนื่องมีลักษณะดังต่อไปนี้:

การแจกแจงแบบสม่ำเสมอแบบไม่ต่อเนื่องถูกกำหนดโดยพารามิเตอร์จำนวนเต็มสองตัว a และ b ซึ่งกำหนดช่วงของค่าที่เป็นไปได้ของการแจกแจง

$\begin{array}{c} X\sim \text{Uniforme}(a,b)\\[2ex]b\geq a\\[2ex]n=b-a+1\end{array}$

ค่าเฉลี่ยของการแจกแจงแบบสม่ำเสมอแบบไม่ต่อเนื่องจะเท่ากับผลรวมของพารามิเตอร์ลักษณะเฉพาะสองตัวหารด้วยสอง

$E[X]=\cfrac{a+b}{2}$

ค่ามัธยฐานของการแจกแจงแบบสม่ำเสมอแบบไม่ต่อเนื่องจะเท่ากับค่าเฉลี่ย ดังนั้นจึงคำนวณโดยใช้นิพจน์เดียวกัน:

$Me=\cfrac{a+b}{2}$

ความแปรปรวนของการแจกแจงแบบสม่ำเสมอแบบไม่ต่อเนื่องจะเท่ากับกำลังสองของจำนวนผลลัพธ์ทั้งหมด ลบ 1 หารด้วย 12

$Var(X)=\cfrac{n^2-1}{12}$

การแจกแจงแบบสม่ำเสมอแบบไม่ต่อเนื่องมีความสมมาตรเกี่ยวกับค่าเฉลี่ย ดังนั้น ค่าสัมประสิทธิ์ความเบ้ของการแจกแจงความน่าจะเป็นจึงเป็นศูนย์

$A=0$

ความโด่งของการกระจายเครื่องแบบแบบไม่ต่อเนื่องสามารถคำนวณได้โดยใช้นิพจน์ต่อไปนี้:

$C=-\cfrac{6\cdot (n^2+1)}{5\cdot (n^2+1)}$

การกระจายเครื่องแบบแบบไม่ต่อเนื่องและการกระจายเครื่องแบบอย่างต่อเนื่อง

สุดท้ายนี้ เราจะเห็นว่าอะไรคือความแตกต่างระหว่างการแจกแจงแบบสม่ำเสมอแบบไม่ต่อเนื่องและการแจกแจงแบบต่อเนื่องแบบต่อเนื่อง เนื่องจากเป็นการแจกแจงความน่าจะเป็นสองประเภทที่คล้ายกันแต่มีความแตกต่างอย่างมาก

ความแตกต่างระหว่างการกระจายสม่ำเสมอแบบไม่ต่อเนื่องและการกระจายสม่ำเสมออย่างต่อเนื่องนั้น ขึ้นอยู่กับค่าที่เป็นไปได้ การแจกแจงแบบสม่ำเสมอแบบแยกสามารถรับค่าบางค่าได้ในช่วงเวลาหนึ่งเท่านั้น ในขณะที่การแจกแจงแบบสม่ำเสมอแบบต่อเนื่องสามารถรับค่าใดก็ได้ในช่วงเวลาที่กำหนดไว้

โดยทั่วไป การแจกแจงแบบสม่ำเสมอแบบไม่ต่อเนื่องสามารถรับเฉพาะค่าจำนวนเต็มเท่านั้น ในขณะที่การแจกแจงแบบต่อเนื่องแบบต่อเนื่องสามารถรับค่าทศนิยมได้เช่นกัน

➤ ดู: การกระจายตัวสม่ำเสมออย่างต่อเนื่อง

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม