การกระจายแกมมา

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 3, 2023 ความน่าจะเป็น 0 ความคิดเห็น

บทความนี้จะอธิบายว่าการแจกแจงแกมมาคืออะไร และใช้เพื่ออะไร ดังนั้น คุณจะพบคำจำกัดความของการแจกแจงแกมมา คุณสมบัติของการกระจายตัว และลักษณะการแสดงกราฟิกของมัน

การแจกแจงแกมมาคืออะไร?

การแจกแจงแกมมา เป็นการแจกแจงความน่าจะเป็นแบบต่อเนื่องที่กำหนดโดยพารามิเตอร์ลักษณะเฉพาะสองตัว ได้แก่ α และ แล กล่าวอีกนัยหนึ่ง การแจกแจงแกมมาขึ้นอยู่กับค่าของพารามิเตอร์สองตัว: α คือพารามิเตอร์รูปร่าง และ แล คือพารามิเตอร์มาตราส่วน

สัญลักษณ์ของการแจกแจงแกมมาคืออักษรกรีกตัวพิมพ์ใหญ่ Γ ดังนั้น หากตัวแปรสุ่มเป็นไปตามการแจกแจงแกมมา มันจะเขียนได้ดังนี้:

$X\sim \Gamma(\alpha,\lambda)$

การแจกแจงแกมมายังสามารถกำหนดพารามิเตอร์ได้โดยใช้พารามิเตอร์รูปร่าง k = α และพารามิเตอร์สเกลผกผัน θ = 1/แล ในทุกกรณี พารามิเตอร์สองตัวที่กำหนดการแจกแจงแกมมาเป็นจำนวนจริงบวก

โดยทั่วไปแล้ว การแจกแจงแกมมาจะใช้ในการสร้างแบบจำลองชุดข้อมูลที่เบ้ขวา เพื่อให้ข้อมูลทางด้านซ้ายของกราฟมีความเข้มข้นมากขึ้น ตัวอย่างเช่น การแจกแจงแกมมาใช้เพื่อจำลองความน่าเชื่อถือของส่วนประกอบไฟฟ้า

แผนภาพการกระจายแกมมา

กราฟของการแจกแจงแกมมาขึ้นอยู่กับค่าของพารามิเตอร์ลักษณะเฉพาะ ด้านล่างนี้ คุณจะเห็นว่าฟังก์ชันความหนาแน่นของการแจกแจงแกมมาแตกต่างกันอย่างไร โดยขึ้นอยู่กับพารามิเตอร์รูปร่างและพารามิเตอร์มาตราส่วน

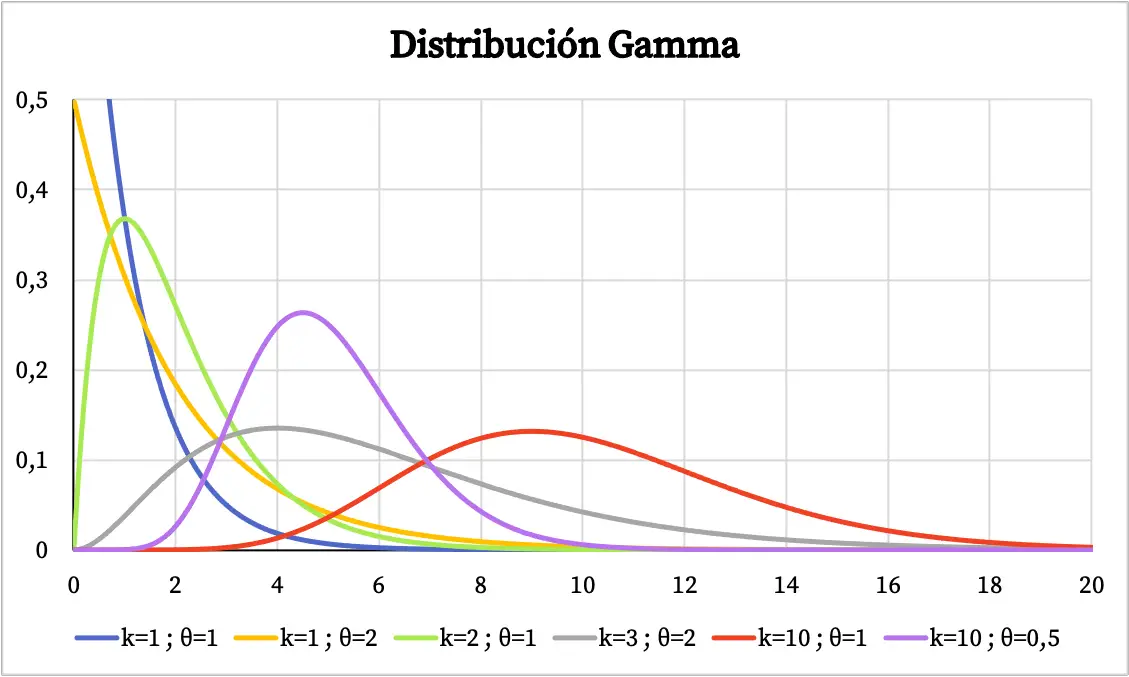
ในทางกลับกัน คุณสามารถดูกราฟของฟังก์ชันความน่าจะเป็นสะสมของการแจกแจงแกมมาได้ด้านล่าง:

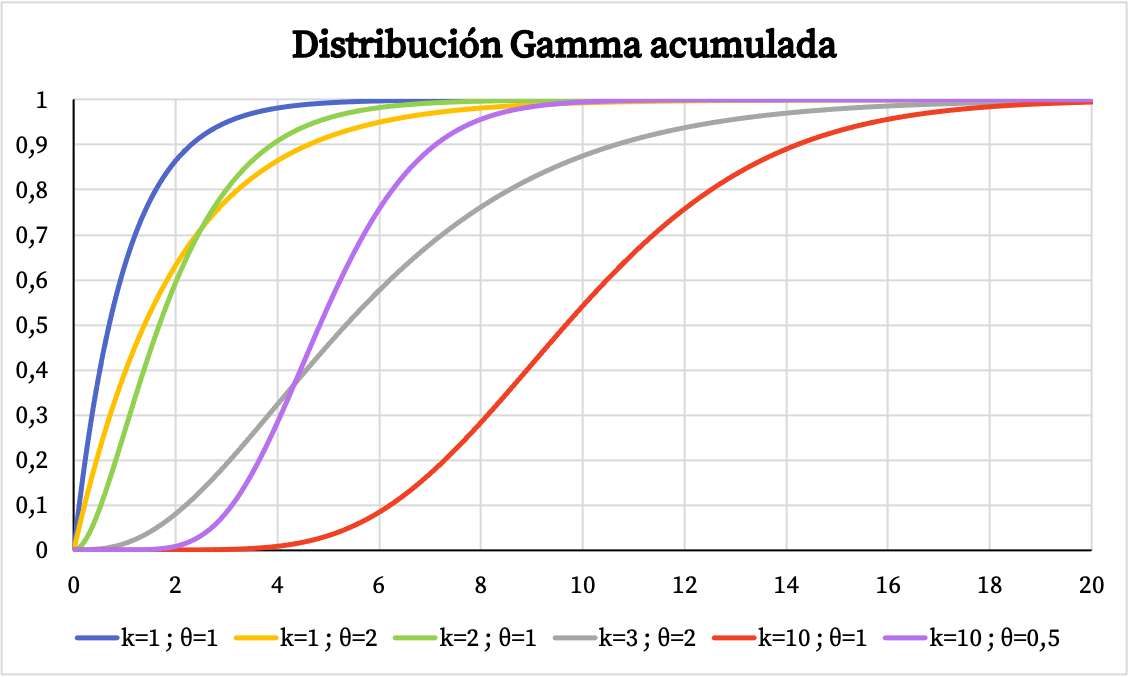
กราฟของฟังก์ชันความน่าจะเป็นสะสมของการแจกแจงแบบแกมม์

ลักษณะเฉพาะของการแจกแจงแกมมา

เราจะมาดูกันว่าคุณลักษณะของการแจกแจงแกมมาคืออะไร

กราฟของการแจกแจงแกมมาถูกกำหนดโดยพารามิเตอร์ลักษณะเฉพาะสองตัว: α คือพารามิเตอร์รูปร่าง และ γ คือพารามิเตอร์มาตราส่วน

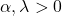
$\alpha , \lambda >0″ title=”Rendered by QuickLaTeX.com” height=”16″ width=”62″ style=”vertical-align: -4px;”></p> </p> <ul> <li> โดเมนของการแจกแจงแกมมาประกอบด้วยจำนวนบวกเท่านั้น</li> </ul> <p class=$ $x\in (0,+\infty)$

ค่าเฉลี่ยของการแจกแจงแกมมาเท่ากับอัตราส่วนระหว่างพารามิเตอร์รูปร่างและพารามิเตอร์สเกล เช่น α/แล

$E[X]=\cfrac{\alpha}{\lambda}$

ความแปรปรวนของการแจกแจงแกมมาเทียบเท่ากับพารามิเตอร์รูปร่างหารด้วยกำลังสองของพารามิเตอร์มาตราส่วน

$Var(X)=\cfrac{\alpha}{\lambda^2}$

สำหรับค่า α น้อยกว่า 1 โหมดจะเป็น 0 แต่ถ้า α เท่ากับหรือมากกว่า 1 โหมดของการแจกแจงแกมมาสามารถคำนวณได้ด้วยสูตรต่อไปนี้:

$\begin{array}{c}Mo=0 \qquad \text{para } \alpha<1\\[2ex]Mo=\cfrac{\alpha-1}{\lambda} \qquad \text{para } \alpha\geq1\end{array}$

สูตรสำหรับฟังก์ชันความหนาแน่นของการแจกแจงแกมมาคือ:

$\displaystyle f(x)=\frac{\lambda(\lambda x)^{\alpha-1}e^{-\lambda x}}{\Gamma(\alpha)}$

โดยที่ Γ คือฟังก์ชันแกมมา ซึ่งกำหนดเป็น:

$\displaystyle \Gamma(\alpha)=\int_0^\infty t^{\alpha-1}e^{-t}dt$

สูตรสำหรับการแจกแจงสะสมของตัวแปรสุ่มที่กำหนดโดยการแจกแจงแกมมาเป็นดังนี้:

$\displaystyle F(x)=\int_0^x\frac{\lambda(\lambda y)^{\alpha-1}e^{-\lambda y}}{\Gamma(\alpha)}\;dy$

หากพารามิเตอร์รูปร่าง α เท่ากับ 1 การแจกแจงแกมมาจะเทียบเท่ากับการแจกแจงแบบเอกซ์โปเนนเชียลด้วยพารามิเตอร์สเกลเดียวกัน แล

$X\sim \Gamma(1,\lambda) \ \color{orange}\bm{\longrightarrow}\color{black} \ X\sim \text{Exp}(\lambda)$

เมื่อพารามิเตอร์มาตราส่วน แล เป็นค่าเฉลี่ย การแจกแจงแกมมาจะเป็นกรณีพิเศษของ การแจกแจงแบบไคสแควร์

$\displaystyle X\sim \Gamma\left(\frac{n}{2},\frac{1}{2}\right) \text{con } n\in \mathbb{N}\ \color{orange}\bm{\longrightarrow}\color{black} \ X\sim \chi_n^2$

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม

การแจกแจงแกมมาคืออะไร?

แผนภาพการกระจายแกมมา

ลักษณะเฉพาะของการแจกแจงแกมมา

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

เพิ่มความคิดเห็น