เมทริกซ์การจัดลำดับความสำคัญ (หรือเมทริกซ์ลำดับความสำคัญ)

บทความนี้จะอธิบายว่าเมทริกซ์การจัดลำดับความสำคัญหรือที่เรียกว่าเมทริกซ์ลำดับความสำคัญคืออะไร คุณลักษณะของเมทริกซ์คืออะไร และใช้เพื่ออะไร ในทำนองเดียวกัน คุณจะเห็นวิธีสร้างเมทริกซ์การจัดลำดับความสำคัญ และยังมีตัวอย่างที่อธิบายทีละขั้นตอนอีกด้วย

เมทริกซ์การจัดลำดับความสำคัญคืออะไร?

เมทริกซ์การจัดลำดับความสำคัญ (หรือ เมทริกซ์ลำดับความสำคัญ ) เป็นเมทริกซ์ที่ช่วยให้คุณสามารถเปรียบเทียบตัวเลือกต่าง ๆ ตามเกณฑ์หลายประการ ดังนั้นจึงใช้เมทริกซ์การจัดลำดับความสำคัญเพื่อประเมินตัวเลือกต่าง ๆ และเลือกตัวเลือกอย่างเป็นกลาง

กล่าวคือ ในเมทริกซ์การจัดลำดับความสำคัญ ตัวเลือกต่างๆ ที่มีอยู่จะถูกจัดประเภทตามคะแนนที่ได้รับตามเกณฑ์ที่เลือกไว้ก่อนหน้านี้ ด้วยวิธีนี้ การตัดสินใจจึงสามารถทำได้ตามวิธีการที่เป็นกลาง

โดยทั่วไปแล้ว แต่ละแถวของเมทริกซ์จะเป็นตัวเลือกให้เลือก ในขณะที่คอลัมน์ของเมทริกซ์จะแสดงถึงเกณฑ์การเลือก ดังนั้น กล่องที่แถวและคอลัมน์ตัดกันคือคะแนนที่ตัวเลือกนี้ได้รับตามเกณฑ์นี้

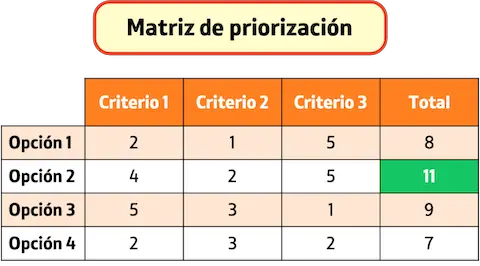
เมทริกซ์การจัดลำดับความสำคัญเรียกอีกอย่างว่า เมทริกซ์หลายเกณฑ์ หรือ แผนภาพการจัดลำดับความสำคัญ

วิธีสร้างเมทริกซ์การจัดลำดับความสำคัญ

ขั้นตอนในการสร้างเมทริกซ์การจัดลำดับความสำคัญมีดังนี้:

1. กำหนดวัตถุประสงค์ของเมทริกซ์การจัดลำดับความสำคัญ : ก่อนที่จะเริ่มสร้างเมทริกซ์การจัดลำดับความสำคัญ วัตถุประสงค์ของการสร้างเมทริกซ์จะต้องชัดเจน วิธีนี้จะทำให้เลือกเกณฑ์ได้ง่ายขึ้น
2. ระบุตัวเลือก : จัดทำรายการตัวเลือกที่เป็นไปได้ทั้งหมดที่จำเป็นต้องได้รับการประเมิน ในบางกรณี ตัวเลือกต่างๆ จะได้รับการกำหนดไว้แล้ว ในขณะที่ในกรณีอื่นๆ คุณจะต้องใช้ไหวพริบและคิดหาทางเลือกอื่น
3. สร้างเกณฑ์ : เกณฑ์ที่เลือกให้คะแนนตัวเลือกต่างๆ ควรสอดคล้องกับวัตถุประสงค์ของเมทริกซ์การจัดลำดับความสำคัญ ซึ่งเป็นเหตุผลว่าทำไมการกำหนดวัตถุประสงค์ของเมทริกซ์อย่างชัดเจนจึงเป็นสิ่งสำคัญ นอกจากนี้จะต้องป้อนเฉพาะเกณฑ์ที่เกี่ยวข้องกับโครงการเท่านั้น เกณฑ์มากเกินไปอาจส่งผลให้ตัวเลือกที่เลือกไม่เหมาะสมที่สุด
4. ถ่วงน้ำหนักเกณฑ์ : เมื่อกำหนดเกณฑ์ที่แตกต่างกันแล้ว จะต้องถ่วงน้ำหนักตามความสำคัญของแต่ละเกณฑ์ โดยปกติจะทำเป็นเปอร์เซ็นต์ ดังนั้นเกณฑ์ที่สำคัญกว่าจะสอดคล้องกับเปอร์เซ็นต์ที่สูงกว่า และผลรวมของน้ำหนักทั้งหมดจะเป็น 1 (หรือ 100%)
5. ประเมินตัวเลือก – แต่ละตัวเลือกควรได้รับคะแนนสำหรับแต่ละเกณฑ์ ขอแนะนำให้ช่วงของคะแนนทั้งหมดเท่ากัน เนื่องจากความแตกต่างในความสำคัญของเกณฑ์ถูกกำหนดไว้แล้วตามน้ำหนัก
6. เลือกตัวเลือกที่ดีที่สุด : หลังจากให้คะแนนตัวเลือกทั้งหมดสำหรับแต่ละเกณฑ์แล้ว คะแนนทั้งหมดที่ได้รับจะถูกรวมเข้าด้วยกัน ตามทฤษฎีแล้วตัวเลือกที่ดีที่สุดคือตัวเลือกที่มีคะแนนมากที่สุด

ตัวอย่างเมทริกซ์การจัดลำดับความสำคัญ

หลังจากดูคำจำกัดความของเมทริกซ์การจัดลำดับความสำคัญและวิธีการดำเนินการแล้ว เราจะเห็นตัวอย่างทีละขั้นตอนเพื่อสิ้นสุดการหลอมรวมแนวคิด

• ธนาคารต้องการลงทุนโดยการซื้อธุรกิจขนาดเล็กโดยมีเป้าหมายเพื่อขยายธุรกิจแล้วขายต่อในราคาที่สูงขึ้น หลังจากผ่านการกรองทางเศรษฐกิจหลายครั้ง บริษัทที่กำลังพิจารณาซื้อคือบริษัท A บริษัท B และบริษัท C

เพื่อวิเคราะห์ว่าบริษัทใดดีที่สุดสำหรับธนาคารที่จะซื้อ เราจะสร้างเมทริกซ์การจัดลำดับความสำคัญ ในกรณีนี้ เราทราบวัตถุประสงค์และตัวเลือกต่างๆ ของเมทริกซ์แล้ว:

วัตถุประสงค์: ซื้อธุรกิจขนาดเล็กเพื่อขายต่อเพื่อให้ได้เงินมากขึ้นและทำให้การลงทุนมีกำไร

ความเป็นไปได้:

• ตัวเลือกที่ 1: บริษัท A
• ตัวเลือกที่ 2: บริษัท B
• ตัวเลือกที่ 3: บริษัท C

เพื่อประเมินตัวเลือกต่างๆ เราจะใช้เกณฑ์การคัดเลือกต่อไปนี้:

เกณฑ์:

• เกณฑ์ที่ 1: ราคาซื้อ ตามตรรกะ ยิ่งราคาเข้าซื้อกิจการของบริษัทต่ำลง จะยิ่งเป็นประโยชน์ต่อธนาคารมากขึ้นเนื่องจากใช้เงินน้อยลง
• หลักเกณฑ์ 2: ศักยภาพในการเติบโต ต้องคำนึงถึงศักยภาพในการเติบโตและมูลค่าที่เพิ่มขึ้นของบริษัทด้วย เนื่องจากธนาคารจะได้รับผลตอบแทนทางเศรษฐกิจที่มากขึ้น
• เกณฑ์ที่ 3: ความเสี่ยงของการล้มละลาย นอกจากนี้ยังจำเป็นต้องคำนึงถึงความเสี่ยงที่แต่ละบริษัทจะล้มละลาย เนื่องจากในกรณีนี้ธนาคารจะสูญเสียเงินที่ลงทุนทั้งหมด ยิ่งคะแนนตามเกณฑ์นี้สูงเท่าไร ความเสี่ยงในการปิดบริษัทก็จะยิ่งน้อยลงเท่านั้น
• หลักเกณฑ์ที่ 4: กำไรประจำปีของบริษัท ต้องประเมินกำไรประจำปีของบริษัทด้วย เนื่องจากเป็นเงินเพิ่มเติมที่ธนาคารจะได้รับนอกเหนือจากกำไรจากการซื้อและขายของบริษัท

ตอนนี้เรารู้เกณฑ์ที่เราจะใช้ในเมทริกซ์การจัดลำดับความสำคัญแล้ว เราจะชั่งน้ำหนักเกณฑ์เหล่านั้นตามความเกี่ยวข้อง

การถ่วงน้ำหนักเกณฑ์:

• เกณฑ์ที่ 1: ราคาซื้อ → 30%
• เกณฑ์ที่ 2: ศักยภาพในการเติบโต → 40%
• เกณฑ์ที่ 3: ความเสี่ยงของการล้มละลาย → 20%
• เกณฑ์ที่ 4: กำไรประจำปีของบริษัท → 10%

เมื่อเราถ่วงน้ำหนักเกณฑ์แล้ว เราจะเตรียมเมทริกซ์การจัดลำดับความสำคัญตามการให้คะแนน ในการดำเนินการนี้ แต่ละตัวเลือกจะได้รับการจัดอันดับตั้งแต่ 1 ถึง 10 สำหรับแต่ละเกณฑ์ จากนั้นจึงเพิ่มคะแนนตามการถ่วงน้ำหนักของเกณฑ์

ประเมินตัวเลือกและเลือกตัวเลือกที่ดีที่สุด:

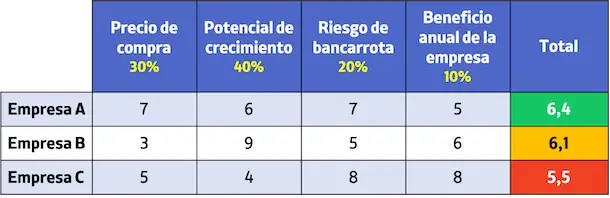
โดยสรุป หลังจากประเมินแต่ละบริษัทตามเกณฑ์ต่างๆ ที่กำหนดแล้ว ธนาคารควรซื้อบริษัท A เนื่องจากเป็นบริษัทที่ได้คะแนนดีที่สุด

เมทริกซ์การจัดลำดับความสำคัญใช้ทำอะไร?

ด้านล่างนี้เราจะให้ข้อมูลสรุปเกี่ยวกับประโยชน์และเวลาที่คุณสามารถใช้เมทริกซ์การจัดลำดับความสำคัญได้

• ระบุเกณฑ์การตัดสินใจ – การกำหนดเกณฑ์การคัดเลือกช่วยให้คุณเห็นสิ่งที่สำคัญที่สุดสำหรับโครงการและสิ่งที่ควรตัดสินใจตาม
• การชี้แจงปัญหา : การเลือกเกณฑ์การตัดสินใจช่วยให้คุณมีความคิดที่ชัดเจนยิ่งขึ้นเกี่ยวกับปัญหาที่แท้จริงที่คุณกำลังเผชิญอยู่และประเด็นที่สำคัญที่สุดในการแก้ไข
• การวิเคราะห์ตัวเลือก : เมทริกซ์การจัดลำดับความสำคัญช่วยอำนวยความสะดวกในการวิเคราะห์ตัวเลือกทั้งหมด เนื่องจากช่วยให้มองเห็นคะแนนของแต่ละตัวเลือกในแต่ละเกณฑ์ได้อย่างรวดเร็ว
• ค้นหาโอกาสในการปรับปรุง : เมื่อเรียกใช้เมทริกซ์การจัดลำดับความสำคัญ คุณสามารถสรุปได้ว่าตัวเลือกหนึ่งดีที่สุดสำหรับโครงการของคุณ หรือในทางกลับกัน คุณต้องสำรวจตัวเลือกใหม่ที่ปรับปรุงผลลัพธ์ที่ได้รับในเมทริกซ์

ข้อดีและข้อเสียของเมทริกซ์การจัดลำดับความสำคัญ

ข้อได้เปรียบ:

• เมทริกซ์การจัดลำดับความสำคัญเป็นเครื่องมือที่ใช้งานง่าย นอกจากนี้ ตัวเลือก เกณฑ์ หรือการถ่วงน้ำหนักสามารถอัปเดตและแก้ไขได้อย่างรวดเร็ว
• มีประโยชน์มากสำหรับการจัดการโครงการเพราะช่วยให้คุณสามารถวิเคราะห์หลายตัวเลือกและตัดสินใจว่าตัวเลือกใดดีที่สุด ช่วยประหยัดเวลา
• นี่เป็นวิธีการที่เป็นกลาง ดังนั้นอคติใดๆ ที่บุคคลอาจมีลดลง
• เมทริกซ์การจัดลำดับความสำคัญนั้นง่ายต่อการเข้าใจทั้งสำหรับผู้ที่ดำเนินการและสำหรับผู้ที่ตีความ

ข้อเสีย:

• ผลลัพธ์ที่ได้ขึ้นอยู่กับการประเมินตนเองของเกณฑ์และการถ่วงน้ำหนัก ดังนั้นทีมจึงต้องเป็นกลาง
• เมทริกซ์การจัดลำดับความสำคัญอาจเข้มงวดเกินไป ขึ้นอยู่กับประเภทขององค์กร
• บางครั้งตัวเลือกสองตัวขึ้นไปมีคะแนนใกล้เคียงกันมาก ดังนั้นจึงไม่มีความชัดเจนว่าจะต้องตัดสินใจอย่างไร ในกรณีนี้ ขอแนะนำให้ทำซ้ำเมทริกซ์ลำดับความสำคัญโดยใช้เกณฑ์และน้ำหนักอื่นๆ