วิธีดำเนินการแปลง box-cox ใน sas

การแปลงแบบ box-cox เป็นวิธีการที่ใช้กันทั่วไปในการแปลงชุดข้อมูลที่ไม่กระจายแบบปกติให้เป็นชุด แบบกระจายแบบปกติ มากขึ้น

แนวคิดพื้นฐานเบื้องหลังวิธีนี้คือการหาค่าของ γ เพื่อให้ข้อมูลที่แปลงแล้วใกล้เคียงกับการแจกแจงแบบปกติมากที่สุด โดยใช้สูตรต่อไปนี้

• y(แลมบ์ดา) = (y ^แลม – 1) / แลม ถ้า y ≠ 0
• y(แลมบ์ดา) = log(y) ถ้า y = 0

เราสามารถระบุค่าที่เหมาะสมที่สุดที่จะใช้สำหรับ แล ใน SAS ได้โดยใช้ขั้นตอน PROC TRANSREG

ตัวอย่างต่อไปนี้แสดงวิธีการใช้ขั้นตอนนี้ในทางปฏิบัติ

ตัวอย่าง: การแปลง Box-Cox ใน SAS

สมมติว่าเรามีชุดข้อมูลต่อไปนี้ใน SAS:

 /*create dataset*/
data my_data;
    input xy;
    datalines ;
7 1
7 1
8 1
3 2
2 2
4 2
4 2
6 2
6 2
7 3
5 3
3 3
3 6
5 7
8 8
;
run;

/*view dataset*/
proc print data =my_data;

สมมติว่าเราใช้ PROC REG เพื่อให้พอดีกับแบบจำลองการถดถอยเชิงเส้นอย่างง่ายกับชุดข้อมูลนี้ โดยใช้ x เป็นตัวแปรทำนายและ y เป็นตัวแปรตอบสนอง

 /*fit simple linear regression model*/
proc reg data =my_data;
    model y = x;
run ;

ในแผนภาพวินิจฉัยผลลัพธ์ เราสามารถแสดง แผนภาพ Residual กับ Quantile (แผนภาพซ้ายสุดในแถวกลาง) เพื่อดูว่าส่วนที่เหลือมีการกระจายตามปกติโดยประมาณในแบบจำลองหรือไม่:

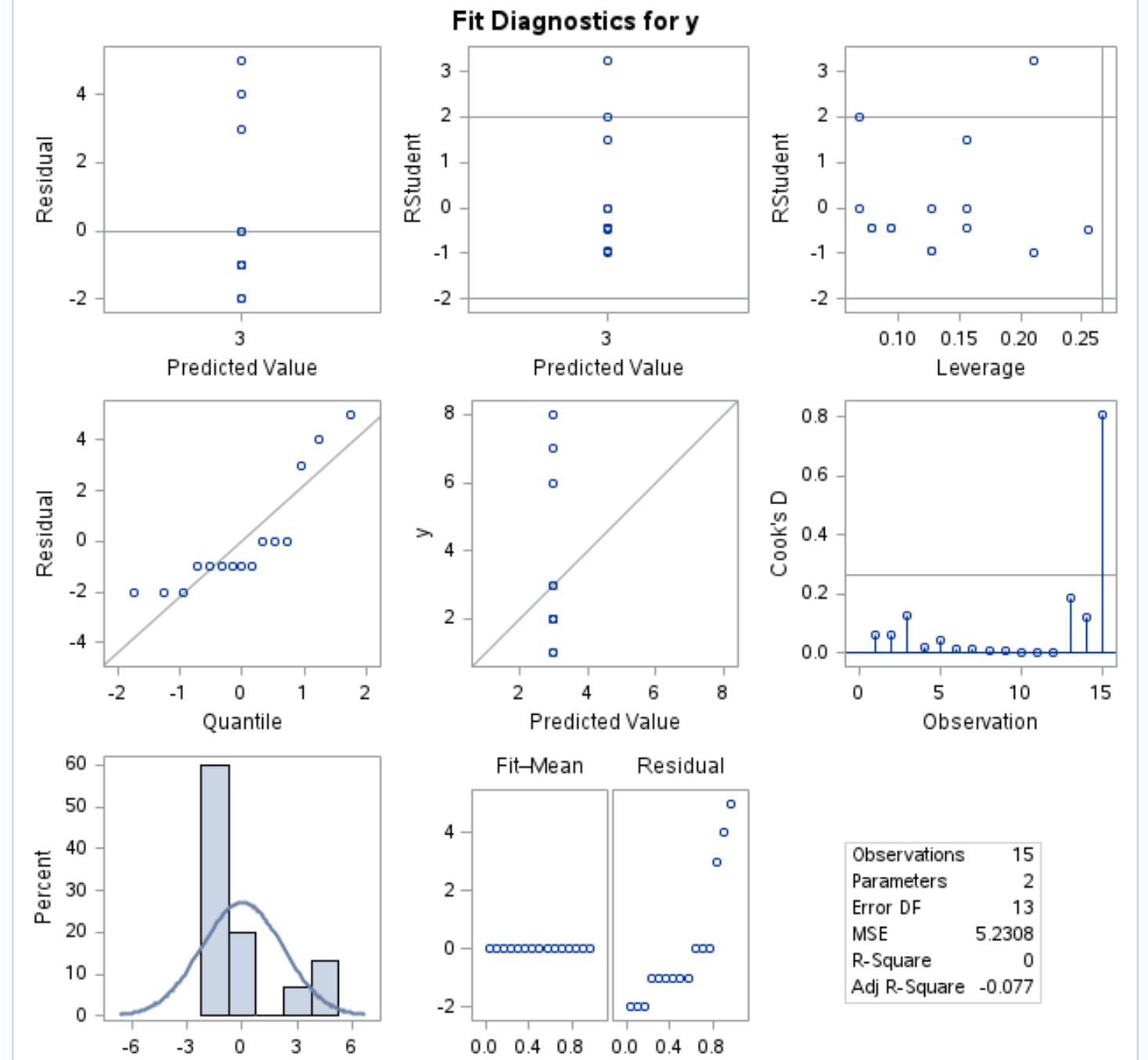
หาก ส่วนที่เหลือ อยู่ประมาณตามแนวเส้นทแยงมุมด้านขวาของกราฟ โดยทั่วไปเราจะถือว่าส่วนที่เหลือมีการกระจายตามปกติ

จากกราฟเราจะเห็นว่าสารตกค้างไม่ได้ตามแนวเส้นทแยงมุมมากนัก

สิ่งนี้บ่งชี้ว่าตัวแปรการตอบสนองในแบบจำลองการถดถอยมีแนวโน้มที่จะไม่กระจายตามปกติ

เนื่องจากตัวแปรตอบสนองไม่ได้กระจายตามปกติ เราจึงสามารถใช้ PROC TRANSREG เพื่อระบุค่าสำหรับ γ ที่เราสามารถใช้เพื่อแปลงตัวแปรตอบสนองเพื่อให้มีการกระจายแบบปกติมากขึ้น:

 /*perform box-cox transformation*/
proc transreg data =my_data;
    model boxcox (y) = identity (x);
run ;

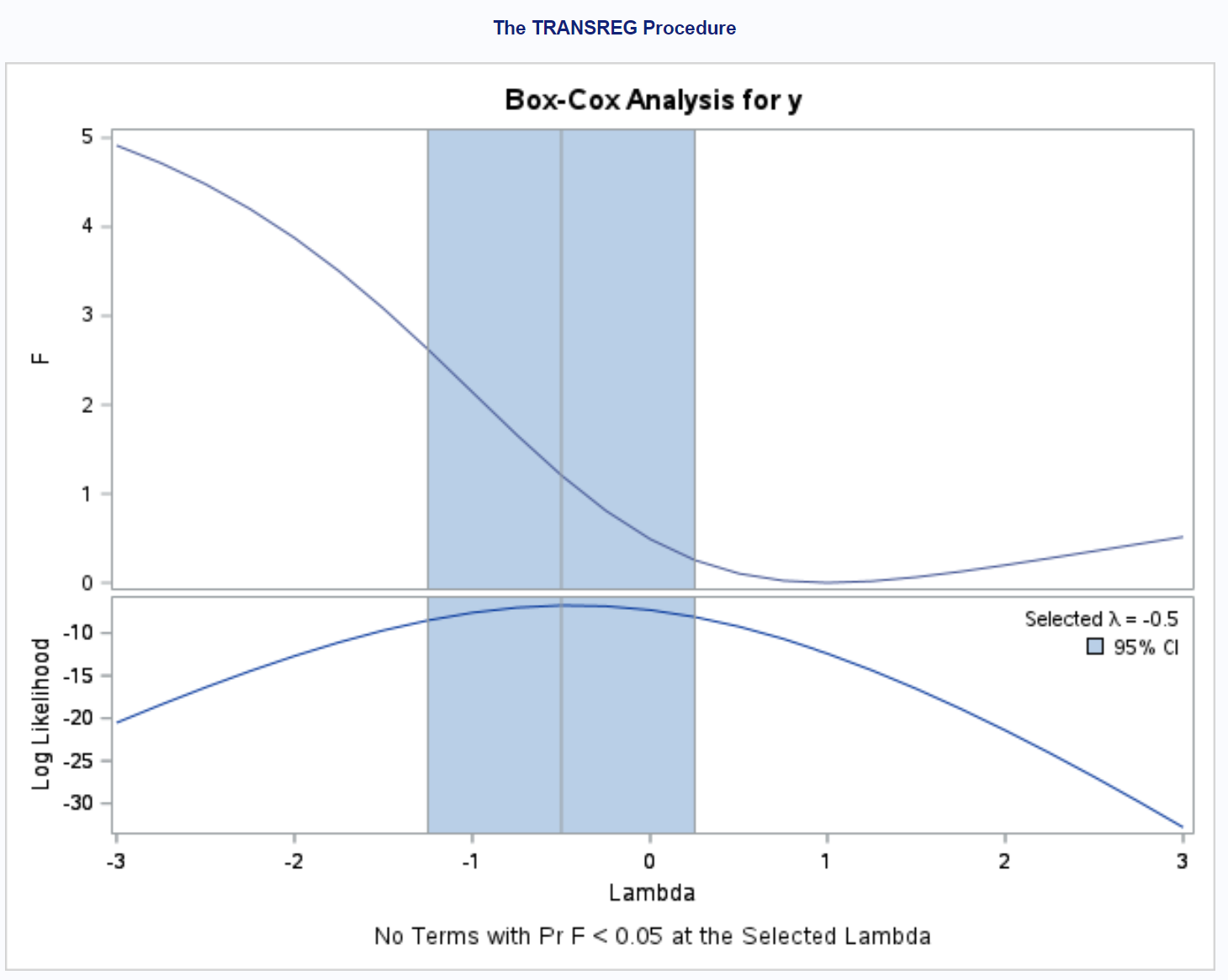
ผลลัพธ์บอกเราว่าค่าที่เลือกที่จะใช้สำหรับ γ คือ – 0.5

ดังนั้น เราสามารถปรับแบบจำลองการถดถอยเชิงเส้นอย่างง่ายได้โดยการแทนที่ตัวแปรตอบสนองเดิม y ด้วยตัวแปร y = (y ^-0.5 – 1) / -0.5

รหัสต่อไปนี้แสดงวิธีการทำเช่นนี้:

 /*create new dataset that uses box-cox transformation to create new y*/
data new_data;
   set my_data;
   new_y = (y**(-0.5) - 1) / -0.5;
run ;

/*fit simple linear regression model using new response variable*/
proc reg data =new_data;
    model new_y = x;
run ;

ใน ส่วนที่เหลือเทียบกับ แผนภาพเชิงปริมาณ ของเอาต์พุตของแบบจำลองนี้ เราจะเห็นว่าส่วนที่เหลืออยู่ใกล้กันมากขึ้นตามเส้นทแยงมุม:

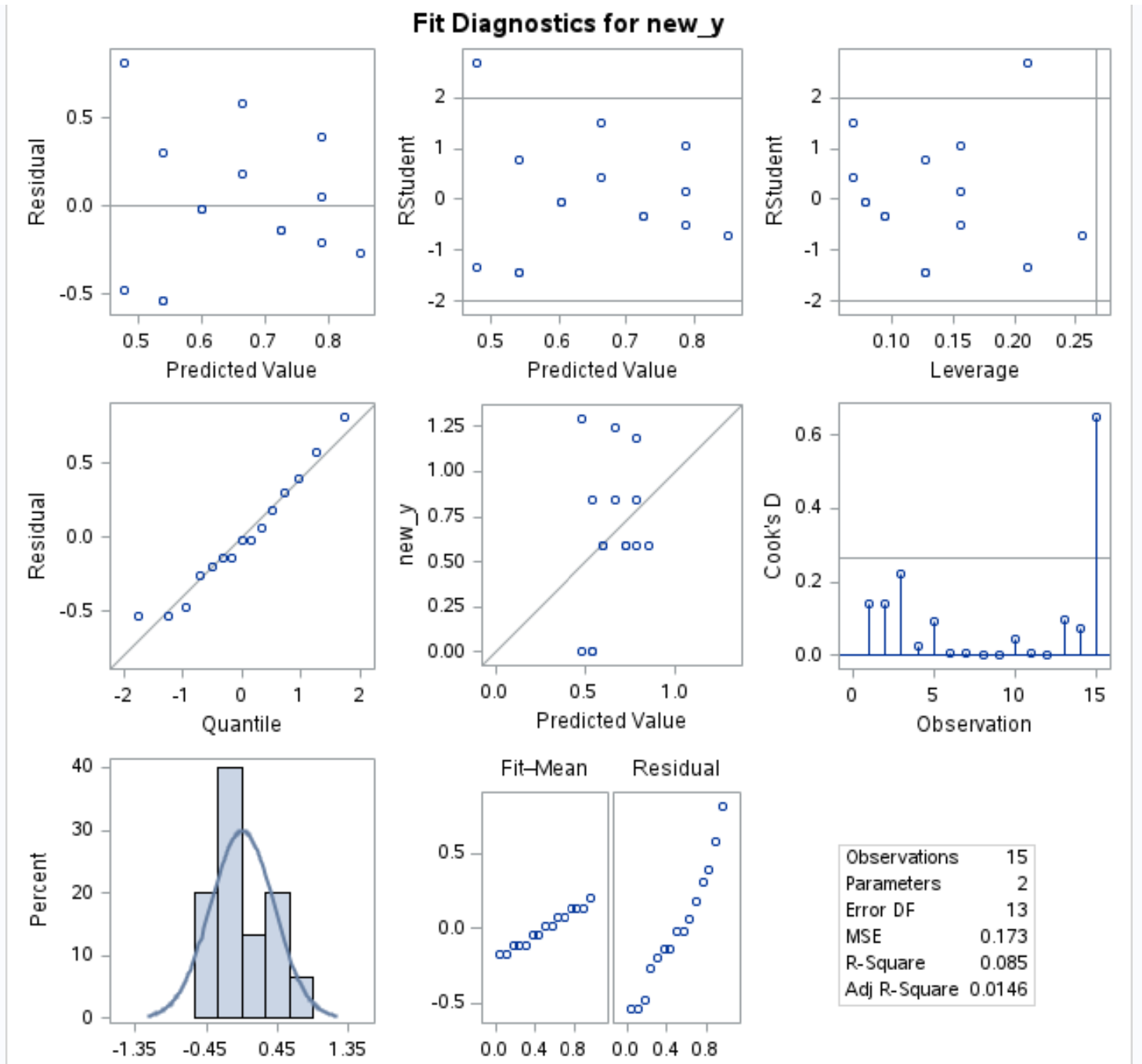
สิ่งนี้บ่งชี้ว่าส่วนที่เหลือของแบบจำลองการแปลงกล่อง-ค็อกซ์นั้นมีการกระจายแบบปกติมากกว่ามาก ซึ่งเป็นไปตาม สมมติฐานหลักข้อใดข้อหนึ่งของการถดถอยเชิงเส้น

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้จะอธิบายวิธีดำเนินการงานทั่วไปอื่นๆ ใน SAS:

วิธีใช้ Proc Univariate สำหรับการทดสอบความเป็นมาตรฐานใน SAS
วิธีสร้างพล็อตคงเหลือใน SAS
วิธีดำเนินการทดสอบ Levene ใน SAS