การถดถอยผ่านจุดกำเนิด: คำจำกัดความและตัวอย่าง

การถดถอยเชิงเส้นอย่างง่ายเป็นวิธีการที่สามารถใช้ในการหาปริมาณความสัมพันธ์ระหว่างตัวแปรทำนายหนึ่งตัวหรือมากกว่ากับ ตัวแปรตอบสนอง

แบบจำลองการถดถอยเชิงเส้นอย่างง่ายมีรูปแบบดังต่อไปนี้:

y = β ₀ + β ₁ x

ทอง:

• y : ค่าของตัวแปรตอบสนอง
• β ₀ : ค่าของตัวแปรตอบสนองเมื่อ x = 0 (เรียกว่าคำว่า “ตัดขวาง”)
• β ₁ : การเพิ่มขึ้นโดยเฉลี่ยของตัวแปรตอบสนองที่เกี่ยวข้องกับการเพิ่มขึ้นของ x หนึ่งหน่วย
• x : ค่าของตัวแปรทำนาย

เวอร์ชันที่แก้ไขของโมเดลนี้เรียกว่า การถดถอยผ่านจุดกำเนิด ซึ่งบังคับให้ y เท่ากับ 0 เมื่อ x เท่ากับ 0

โมเดลประเภทนี้มีรูปแบบดังต่อไปนี้:

y = _β1x

โปรดทราบว่าคำสกัดกั้นได้ถูกลบออกจากแบบจำลองอย่างสมบูรณ์แล้ว

บางครั้งแบบจำลองนี้จะใช้เมื่อนักวิจัยรู้ว่าตัวแปรตอบสนองต้องเป็นศูนย์เมื่อตัวแปรทำนายเป็นศูนย์

ในโลกแห่งความเป็นจริง แบบจำลองประเภทนี้มักใช้ใน การศึกษาป่าไม้หรือนิเวศวิทยา

ตัวอย่างเช่น นักวิจัยสามารถใช้เส้นรอบวงของต้นไม้เพื่อทำนายความสูงของต้นไม้ได้ หากต้นไม้ต้นใดมีเส้นรอบวงเป็นศูนย์ ต้นไม้นั้นจะต้องมีความสูงเป็นศูนย์

ดังนั้น เมื่อปรับแบบจำลองการถดถอยให้เข้ากับข้อมูลนี้ จึงไม่สมเหตุสมผลที่คำเดิมจะเป็นค่าที่ไม่ใช่ศูนย์

ตัวอย่างต่อไปนี้แสดงความแตกต่างระหว่างการปรับแบบจำลองการถดถอยเชิงเส้นแบบธรรมดาให้เหมาะสมกับแบบจำลองที่ใช้การถดถอยผ่านจุดเริ่มต้น

ตัวอย่าง: การถดถอยผ่านจุดกำเนิด

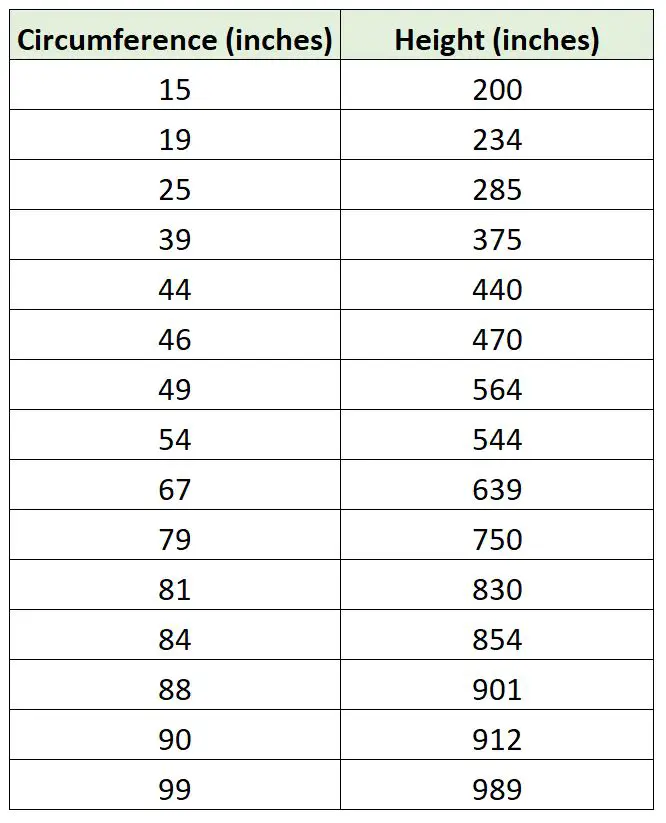
สมมติว่านักชีววิทยาต้องการสร้างแบบจำลองการถดถอยโดยใช้เส้นรอบวงของต้นไม้เพื่อทำนายความสูงของต้นไม้ เธอออกไปและรวบรวมการวัดต่อไปนี้เพื่อเก็บตัวอย่างต้นไม้ 15 ต้น:

เราสามารถใช้โค้ดต่อไปนี้ใน R เพื่อให้พอดีกับโมเดลการถดถอยเชิงเส้นอย่างง่ายกับโมเดลการถดถอยที่ไม่มีจุดตัดและพล็อตเส้นการถดถอยสองเส้น:

 #create data frame
df <- data. frame (circ=c(15, 19, 25, 39, 44, 46, 49, 54, 67, 79, 81, 84, 88, 90, 99),
                 height=c(200, 234, 285, 375, 440, 470, 564, 544, 639, 750, 830, 854,
                          901, 912, 989))

#fit a simple linear regression model
model <- lm(height ~ circ, data = df)

#fit regression through the origin
model_origin <- lm(height ~ 0 + ., data = df)

#create scatterplot
plot(df$circ, df$height, xlab=' Circumference ', ylab=' Height ',
     cex= 1.5 , pch= 16 , ylim=c(0.1000), xlim=c(0.100))

#add the fitted regression lines to the scatterplot
abline(model, col=' blue ', lwd= 2 )
abline(model_origin, lty=' dashed ', col=' red ', lwd= 2 )

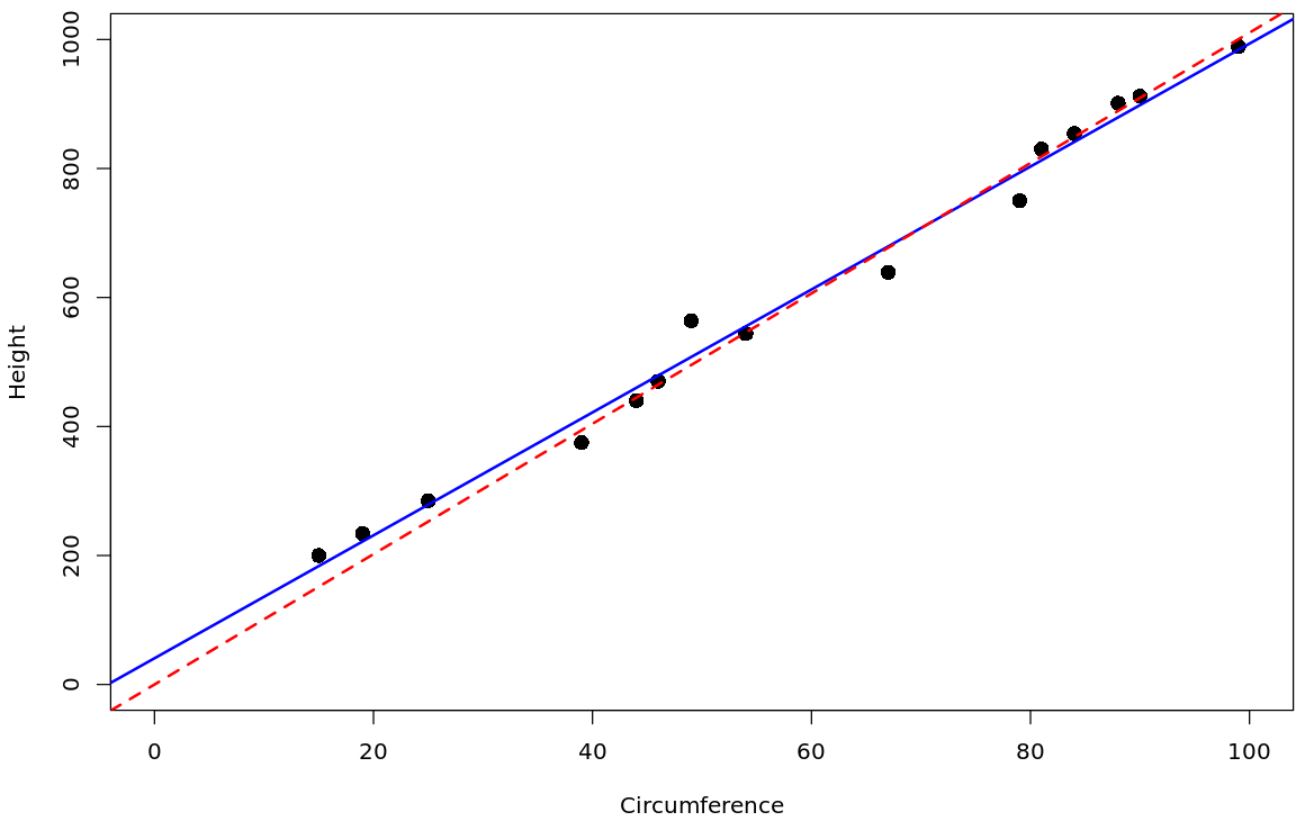
เส้นประสีแดงแสดงถึงแบบจำลองการถดถอยที่ผ่านจุดกำเนิด และเส้นทึบสีน้ำเงินแสดงถึงแบบจำลองการถดถอยเชิงเส้นแบบธรรมดา

เราสามารถใช้โค้ดต่อไปนี้ใน R เพื่อรับการประมาณค่าสัมประสิทธิ์สำหรับแต่ละรุ่น:

 #display coefficients for simple linear regression model
coef(model)

(Intercept) circ 
  40.696971 9.529631 

#display coefficients for regression model through the origin
coef(model_origin)

    circ 
10.10574 

สมการที่พอดีสำหรับแบบจำลองการถดถอยเชิงเส้นอย่างง่ายคือ:

ความสูง = 40.6969 + 9.5296 (เส้นรอบวง)

และสมการที่พอดีสำหรับแบบจำลองการถดถอยผ่านจุดกำเนิดคือ:

ส่วนสูง = 10.1057 (เส้นรอบวง)

โปรดทราบว่าการประมาณค่าสัมประสิทธิ์สำหรับตัวแปรเส้นรอบวงจะแตกต่างกันเล็กน้อย

ข้อควรระวังในการใช้การถดถอยผ่านจุดเริ่มต้น

ก่อนที่จะใช้การถดถอยแบบสกัดกั้น คุณต้องแน่ใจอย่างแน่นอนว่าค่า 0 สำหรับตัวแปรทำนายหมายถึงค่า 0 สำหรับตัวแปรการตอบสนอง ในหลาย ๆ สถานการณ์ แทบจะเป็นไปไม่ได้เลยที่จะทราบแน่ชัด

และหากคุณใช้การถดถอยผ่านจุดกำเนิดเพื่อรักษาระดับความอิสระในการประมาณค่าจุดกำเนิด ก็แทบจะไม่สร้างความแตกต่างอย่างมีนัยสำคัญหากขนาดตัวอย่างของคุณใหญ่พอ

หากคุณเลือกที่จะใช้การถดถอยผ่านจุดเริ่มต้น อย่าลืมสรุปเหตุผลของคุณในการวิเคราะห์หรือรายงานขั้นสุดท้าย

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้ให้ข้อมูลเพิ่มเติมเกี่ยวกับการถดถอยเชิงเส้น:

รู้เบื้องต้นเกี่ยวกับการถดถอยเชิงเส้นอย่างง่าย
รู้เบื้องต้นเกี่ยวกับการถดถอยเชิงเส้นพหุคูณ
วิธีอ่านและตีความตารางการถดถอย