การถดถอยองค์ประกอบหลักใน python (ทีละขั้นตอน)

เมื่อกำหนดชุดของตัวแปรทำนาย p และตัวแปร ตอบสนอง การถดถอยเชิงเส้นพหุคูณ จะใช้วิธีที่เรียกว่า กำลังสองน้อยที่สุด เพื่อลดผลรวมที่เหลือของกำลังสอง (RSS):

RSS = Σ(ฉัน _ฉัน – ŷ _ฉัน ) ²

ทอง:

• Σ : สัญลักษณ์กรีกหมายถึง ผลรวม
• y _i : ค่าตอบสนองจริงสำหรับการสังเกต ^{ครั้งที่ 3}
• ŷ _i : ค่าตอบสนองที่คาดการณ์ไว้ตามแบบจำลองการถดถอยเชิงเส้นพหุคูณ

อย่างไรก็ตาม เมื่อตัวแปรทำนายมีความสัมพันธ์กันสูง ความเป็นหลายคอลลิเนียร์ อาจกลายเป็นปัญหาได้ ซึ่งอาจทำให้การประมาณค่าสัมประสิทธิ์แบบจำลองไม่น่าเชื่อถือและแสดงความแปรปรวนสูง

วิธีหนึ่งที่จะหลีกเลี่ยงปัญหานี้คือการใช้ การถดถอยองค์ประกอบหลัก ซึ่งจะค้นหาชุดค่าผสมเชิงเส้น M (เรียกว่า “ส่วนประกอบหลัก”) ของตัวทำนาย p ดั้งเดิม จากนั้นใช้กำลังสองน้อยที่สุดเพื่อให้พอดีกับแบบจำลองการถดถอยเชิงเส้นโดยใช้ส่วนประกอบหลักเป็นตัวทำนาย

บทช่วยสอนนี้ให้ตัวอย่างทีละขั้นตอนของวิธีการดำเนินการถดถอยส่วนประกอบหลักใน Python

ขั้นตอนที่ 1: นำเข้าแพ็คเกจที่จำเป็น

ขั้นแรก เราจะนำเข้าแพ็คเกจที่จำเป็นในการดำเนินการการถดถอยองค์ประกอบหลัก (PCR) ใน Python:

 import numpy as np
import pandas as pd
import matplotlib. pyplot as plt
from sklearn. preprocessing import scale 
from sklearn import model_selection
from sklearn. model_selection import RepeatedKFold
from sklearn.model_selection import train_test_split
from sklearn. PCA import decomposition
from sklearn. linear_model import LinearRegression
from sklearn. metrics import mean_squared_error

ขั้นตอนที่ 2: โหลดข้อมูล

สำหรับตัวอย่างนี้ เราจะใช้ชุดข้อมูลชื่อ mtcars ซึ่งมีข้อมูลเกี่ยวกับรถยนต์ 33 คันที่แตกต่างกัน เราจะใช้ hp เป็นตัวแปรตอบสนอง และตัวแปรต่อไปนี้เป็นตัวทำนาย:

• mpg
• แสดง
• อึ
• น้ำหนัก
• คิววินาที

รหัสต่อไปนี้แสดงวิธีการโหลดและแสดงชุดข้อมูลนี้:

 #define URL where data is located
url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/mtcars.csv"

#read in data
data_full = pd. read_csv (url)

#select subset of data
data = data_full[["mpg", "disp", "drat", "wt", "qsec", "hp"]]

#view first six rows of data
data[0:6]


        mpg disp drat wt qsec hp
0 21.0 160.0 3.90 2.620 16.46 110
1 21.0 160.0 3.90 2.875 17.02 110
2 22.8 108.0 3.85 2.320 18.61 93
3 21.4 258.0 3.08 3.215 19.44 110
4 18.7 360.0 3.15 3.440 17.02 175
5 18.1 225.0 2.76 3.460 20.22 105

ขั้นตอนที่ 3: ปรับโมเดล PCR

รหัสต่อไปนี้แสดงวิธีปรับโมเดล PCR ให้พอดีกับข้อมูลนี้ หมายเหตุสิ่งต่อไปนี้:

• pca.fit_transform(scale(X)) : สิ่งนี้จะบอก Python ว่าตัวแปรทำนายแต่ละตัวควรได้รับการปรับขนาดให้มีค่าเฉลี่ยเป็น 0 และค่าเบี่ยงเบนมาตรฐานเป็น 1 สิ่งนี้ทำให้แน่ใจได้ว่าไม่มีตัวแปรทำนายใดที่มีอิทธิพลมากเกินไปในแบบจำลองหาก สิ่งนี้เกิดขึ้น ที่จะวัดในหน่วยต่างๆ
• cv = RepeatedKFold() : สิ่งนี้จะบอก Python ให้ใช้ การตรวจสอบข้าม k-fold เพื่อประเมินประสิทธิภาพของโมเดล สำหรับตัวอย่างนี้ เราเลือก k = 10 เท่า ทำซ้ำ 3 ครั้ง

 #define predictor and response variables
X = data[["mpg", "disp", "drat", "wt", "qsec"]]
y = data[["hp"]]

#scale predictor variables
pca = pca()
X_reduced = pca. fit_transform ( scale (X))

#define cross validation method
cv = RepeatedKFold(n_splits= 10 , n_repeats= 3 , random_state= 1 )

regr = LinearRegression()
mse = []

# Calculate MSE with only the intercept
score = -1*model_selection. cross_val_score (regr,
           n.p. ones ((len(X_reduced),1)), y, cv=cv,
           scoring=' neg_mean_squared_error '). mean ()    
mse. append (score)

# Calculate MSE using cross-validation, adding one component at a time
for i in np. arange (1, 6):
    score = -1*model_selection. cross_val_score (regr,
               X_reduced[:,:i], y, cv=cv, scoring=' neg_mean_squared_error '). mean ()
    mse. append (score)
    
# Plot cross-validation results    
plt. plot (mse)
plt. xlabel ('Number of Principal Components')
plt. ylabel ('MSE')
plt. title ('hp') 

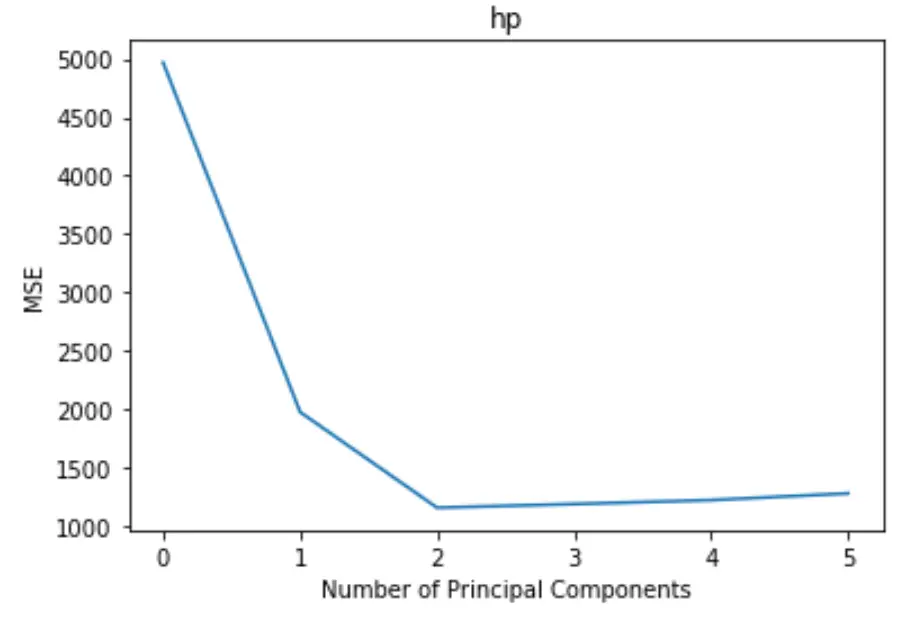
โครงเรื่องจะแสดงจำนวนองค์ประกอบหลักตามแกน x และการทดสอบ MSE (ค่าคลาดเคลื่อนกำลังสองเฉลี่ย) ตามแกน y

จากกราฟ เราจะเห็นว่า MSE ของการทดสอบลดลงโดยการเพิ่มองค์ประกอบหลักสองรายการ แต่จะเริ่มเพิ่มขึ้นเมื่อเราเพิ่มองค์ประกอบหลักมากกว่าสองรายการ

ดังนั้นแบบจำลองที่เหมาะสมที่สุดจึงมีเพียงองค์ประกอบหลักสององค์ประกอบแรกเท่านั้น

นอกจากนี้เรายังสามารถใช้โค้ดต่อไปนี้เพื่อคำนวณเปอร์เซ็นต์ของความแปรปรวนในตัวแปรตอบสนองที่อธิบายโดยการเพิ่มส่วนประกอบหลักแต่ละรายการลงในโมเดล:

 n.p. cumsum (np. round (pca. explained_variance_ratio_ , decimals= 4 )* 100 )

array([69.83, 89.35, 95.88, 98.95, 99.99])

เราสามารถเห็นสิ่งต่อไปนี้:

• การใช้เพียงองค์ประกอบหลักแรกเท่านั้น เราสามารถอธิบายความแปรผันของตัวแปรตอบสนองได้ 69.83%
• ด้วยการเพิ่มองค์ประกอบหลักที่สอง เราสามารถอธิบายความแปรผันของตัวแปรตอบสนองได้ 89.35%

โปรดทราบว่าเรายังคงสามารถอธิบายความแปรปรวนได้มากขึ้นโดยใช้องค์ประกอบหลักมากขึ้น แต่เราเห็นว่าการเพิ่มองค์ประกอบหลักมากกว่า 2 องค์ประกอบจริงๆ แล้วไม่ได้เพิ่มเปอร์เซ็นต์ของความแปรปรวนที่อธิบายไว้มากนัก

ขั้นตอนที่ 4: ใช้แบบจำลองสุดท้ายเพื่อคาดการณ์

เราสามารถใช้แบบจำลอง PCR ส่วนประกอบสองหลักสุดท้ายเพื่อคาดการณ์เกี่ยวกับการสังเกตใหม่

รหัสต่อไปนี้แสดงวิธีแยกชุดข้อมูลดั้งเดิมออกเป็นชุดการฝึกและชุดทดสอบ และใช้แบบจำลอง PCR ที่มีองค์ประกอบหลักสองส่วนเพื่อคาดการณ์ชุดทดสอบ

 #split the dataset into training (70%) and testing (30%) sets
X_train,X_test,y_train,y_test = train_test_split (X,y,test_size= 0.3 , random_state= 0 ) 

#scale the training and testing data
X_reduced_train = pca. fit_transform ( scale (X_train))
X_reduced_test = pca. transform ( scale (X_test))[:,:1]

#train PCR model on training data 
regr = LinearRegression()
reg. fit (X_reduced_train[:,:1], y_train)

#calculate RMSE
pred = regr. predict (X_reduced_test)
n.p. sqrt ( mean_squared_error (y_test, pred))

40.2096

เราเห็นว่าการทดสอบ RMSE กลายเป็น 40.2096 นี่คือค่าเบี่ยงเบนเฉลี่ยระหว่างค่า HP ที่คาดการณ์ไว้กับค่า HP ที่สังเกตได้สำหรับการสังเกตชุดทดสอบ

สามารถดูโค้ด Python แบบเต็มที่ใช้ในตัวอย่างนี้ ได้ ที่นี่