วิธีดำเนินการถดถอยเชิงปริมาณใน r
การถดถอยเชิงเส้นเป็นวิธีการที่เราสามารถใช้เพื่อทำความเข้าใจความสัมพันธ์ระหว่างตัวแปรทำนายตั้งแต่หนึ่งตัวขึ้นไปกับ ตัวแปรตอบสนอง
โดยทั่วไป เมื่อเราทำการถดถอยเชิงเส้น เราต้องการประมาณค่าเฉลี่ยของตัวแปรตอบสนอง
อย่างไรก็ตาม เราสามารถใช้วิธีที่เรียกว่า การถดถอยเชิงควอนไทล์ แทนเพื่อประมาณ ค่า ควอนไทล์หรือค่าเปอร์เซ็นไทล์ของค่าตอบสนอง เช่น เปอร์เซ็นไทล์ที่ 70, เปอร์เซ็นไทล์ที่ 90, เปอร์เซ็นไทล์ที่ 98 เป็นต้น
ในการดำเนินการถดถอยเชิงปริมาณใน R เราสามารถใช้ฟังก์ชัน rq() จากแพ็คเกจ quantreg ซึ่งใช้ไวยากรณ์ต่อไปนี้:
library (quantreg) model <- rq(y ~ x, data = dataset, tau = 0.5 )
ทอง:
- y: ตัวแปรตอบสนอง
- x: ตัวแปรทำนาย
- data: ชื่อของชุดข้อมูล
- เทา: เปอร์เซ็นไทล์ที่จะค้นหา ค่าเริ่มต้นคือค่ามัธยฐาน (tau = 0.5) แต่คุณสามารถตั้งค่าเป็นตัวเลขใดก็ได้ระหว่าง 0 ถึง 1
บทช่วยสอนนี้ให้ตัวอย่างทีละขั้นตอนของวิธีใช้ฟังก์ชันนี้เพื่อดำเนินการถดถอยเชิงควอนไทล์ใน R
ขั้นตอนที่ 1: ป้อนข้อมูล
สำหรับตัวอย่างนี้ เราจะสร้างชุดข้อมูลที่ประกอบด้วยชั่วโมงเรียนและผลการสอบที่ได้รับสำหรับนักศึกษา 100 คนในมหาวิทยาลัย:
#make this example reproducible set.seed(0) #create data frame hours <- runif(100, 1, 10) score <- 60 + 2*hours + rnorm(100, mean=0, sd=.45*hours) df <- data.frame(hours, score) #view first six rows head(df) hours score 1 9.070275 79.22682 2 3.389578 66.20457 3 4.349115 73.47623 4 6.155680 70.10823 5 9.173870 78.12119 6 2.815137 65.94716
ขั้นตอนที่ 2: ดำเนินการถดถอยเชิงปริมาณ
ต่อไป เราจะปรับแบบจำลองการถดถอยเชิงปริมาณโดยใช้ชั่วโมงที่ศึกษาเป็นตัวแปรทำนายและคะแนนการสอบเป็นตัวแปรตอบสนอง
เราจะใช้แบบจำลองเพื่อทำนายคะแนนสอบเปอร์เซ็นไทล์ที่ 90 ที่คาดหวังโดยพิจารณาจากจำนวนชั่วโมงที่เรียน:
library (quantreg) #fit model model <- rq(score ~ hours, data = df, tau = 0.9 ) #view summary of model summary(model) Call: rq(formula = score ~ hours, tau = 0.9, data = df) tau: [1] 0.9 Coefficients: coefficients lower bd upper bd (Intercept) 60.25185 59.27193 62.56459 hours 2.43746 1.98094 2.76989
จากผลลัพธ์เราจะเห็นสมการการถดถอยโดยประมาณ:
คะแนนสอบเปอร์เซ็นไทล์ที่ 90 = 60.25 + 2.437*(ชั่วโมง)
เช่น คะแนนเปอร์เซ็นไทล์ที่ 90 ของนักเรียนทุกคนที่เรียน 8 ชั่วโมงควรเป็น 79.75
คะแนนสอบเปอร์เซ็นไทล์ที่ 90 = 60.25 + 2.437*(8) = 79.75
ผลลัพธ์ยังแสดงขีดจำกัดความเชื่อมั่นบนและล่างสำหรับการสกัดกั้นและเวลาของตัวแปรทำนาย
ขั้นตอนที่ 3: เห็นภาพผลลัพธ์
นอกจากนี้เรายังสามารถแสดงภาพผลลัพธ์การถดถอยได้โดยการสร้างแผนภาพกระจายที่มีสมการการถดถอยควอนไทล์ที่ติดตั้งไว้ซ้อนทับบนกราฟ:
library (ggplot2) #create scatterplot with quantile regression line ggplot(df, aes(hours,score)) + geom_point() + geom_abline(intercept= coef (model)[1], slope= coef (model)[2])
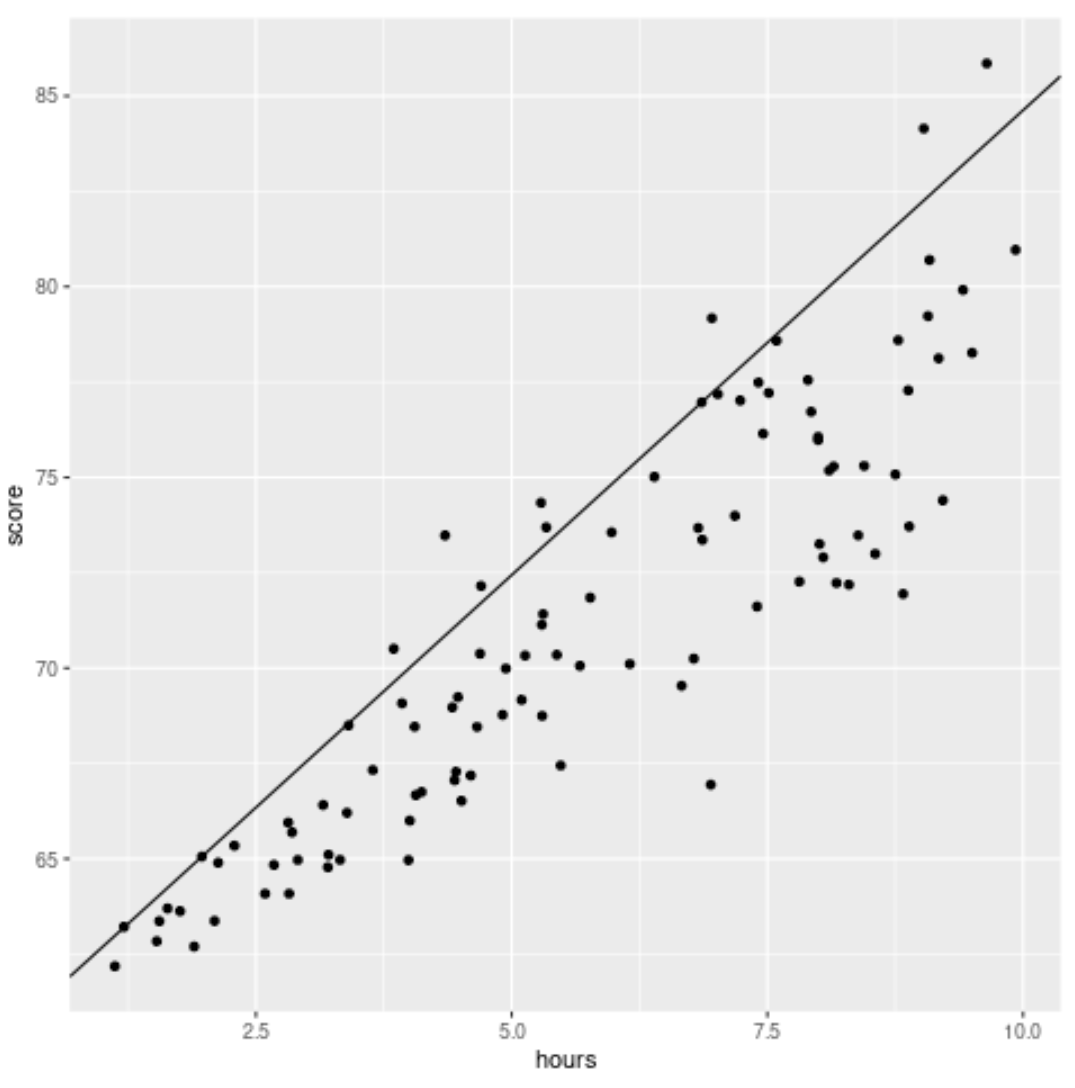
ต่างจากเส้นการถดถอยเชิงเส้นแบบดั้งเดิม โปรดทราบว่าเส้นพอดีนี้ไม่ผ่านใจกลางของข้อมูล แต่จะผ่านเปอร์เซ็นไทล์ที่ 90 โดยประมาณในแต่ละระดับของตัวแปรทำนาย
เราสามารถเห็นความแตกต่างระหว่างสมการการถดถอยควอนไทล์พอดีและสมการถดถอยเชิงเส้นอย่างง่ายโดยการเพิ่มอาร์กิวเมนต์ geom_smooth()
library (ggplot2) #create scatterplot with quantile regression line and simple linear regression line ggplot(df, aes(hours,score)) + geom_point() + geom_abline(intercept= coef (model)[1], slope= coef (model)[2]) + geom_smooth(method=" lm ", se= F )
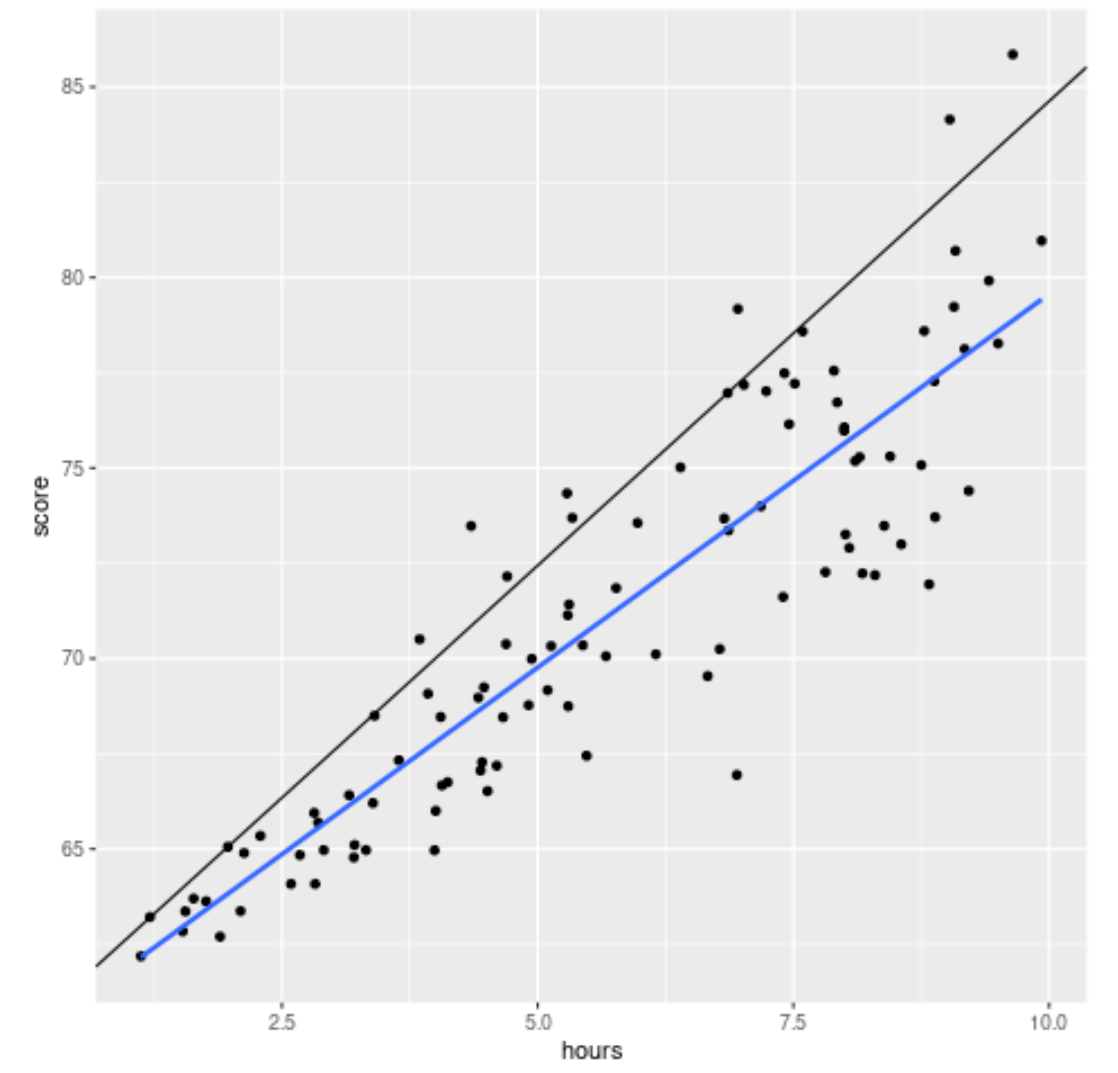
เส้นสีดำแสดงเส้นการถดถอยเชิงปริมาณที่ปรับสำหรับเปอร์เซ็นไทล์ที่ 90 และเส้นสีน้ำเงินแสดงเส้นการถดถอยเชิงเส้นอย่างง่าย ซึ่งประมาณค่าเฉลี่ยของตัวแปรการตอบสนอง
ตามที่คาดไว้ เส้นการถดถอยเชิงเส้นอย่างง่ายจะลากผ่านข้อมูลและแสดงค่าเฉลี่ยโดยประมาณของคะแนนสอบในแต่ละระดับชั่วโมง
แหล่งข้อมูลเพิ่มเติม
บทช่วยสอนต่อไปนี้จะอธิบายวิธีดำเนินการงานทั่วไปอื่นๆ ใน R:
วิธีดำเนินการถดถอยเชิงเส้นอย่างง่ายใน R
วิธีดำเนินการถดถอยเชิงเส้นพหุคูณใน R
วิธีดำเนินการถดถอยกำลังสองใน R