วิธีการดำเนินการถดถอยเชิงเส้นหลายรายการใน excel

การถดถอยเชิงเส้นพหุคูณ เป็นวิธีการที่เราสามารถใช้เพื่อทำความเข้าใจความสัมพันธ์ระหว่างตัวแปรอธิบายตั้งแต่สองตัวขึ้นไปกับ ตัวแปรตอบสนอง

บทช่วยสอนนี้จะอธิบายวิธีการถดถอยเชิงเส้นหลายรายการใน Excel

หมายเหตุ: หากคุณมีตัวแปรอธิบายเพียงตัวแปรเดียว คุณควรดำเนิน การถดถอยเชิงเส้นอย่างง่าย แทน

ตัวอย่าง: การถดถอยเชิงเส้นพหุคูณใน Excel

สมมติว่าเราต้องการทราบว่าจำนวนชั่วโมงที่ใช้ในการศึกษาและจำนวนการสอบเตรียมสอบส่งผลต่อเกรดที่นักเรียนได้รับในการสอบเข้าวิทยาลัยบางประเภทหรือไม่

ในการสำรวจความสัมพันธ์นี้ เราสามารถทำการถดถอยเชิงเส้นพหุคูณโดยใช้ ชั่วโมงการศึกษา และ การสอบเตรียมการที่ใช้ เป็นตัวแปรอธิบาย และ ผลการสอบ เป็นตัวแปรตอบสนอง

ทำตามขั้นตอนต่อไปนี้ใน Excel เพื่อดำเนินการถดถอยเชิงเส้นหลายรายการ

ขั้นตอนที่ 1: ป้อนข้อมูล

ป้อนข้อมูลต่อไปนี้สำหรับจำนวนชั่วโมงที่เรียน การสอบเตรียมสอบ และผลการสอบที่ได้รับสำหรับนักเรียน 20 คน:

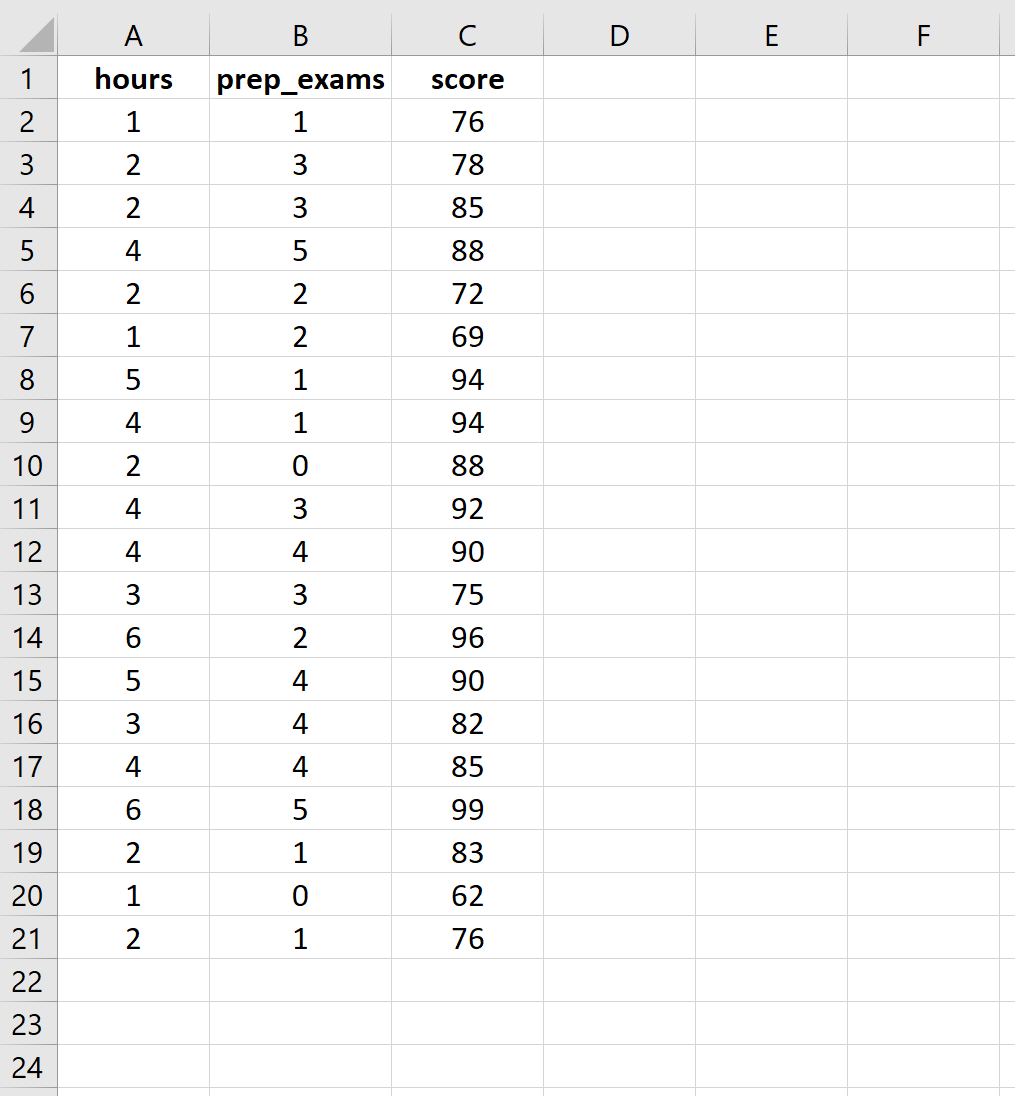
ขั้นตอนที่ 2: ดำเนินการถดถอยเชิงเส้นหลายรายการ

บน Ribbon ด้านบนของ Excel ให้ไปที่แท็บ Data แล้วคลิก Data Analysis หากคุณไม่เห็นตัวเลือกนี้ คุณต้อง ติดตั้งซอฟต์แวร์ Analysis ToolPak ฟรี ก่อน

เมื่อคุณคลิกที่ การวิเคราะห์ข้อมูล หน้าต่างใหม่จะปรากฏขึ้น เลือก การถดถอย แล้วคลิกตกลง

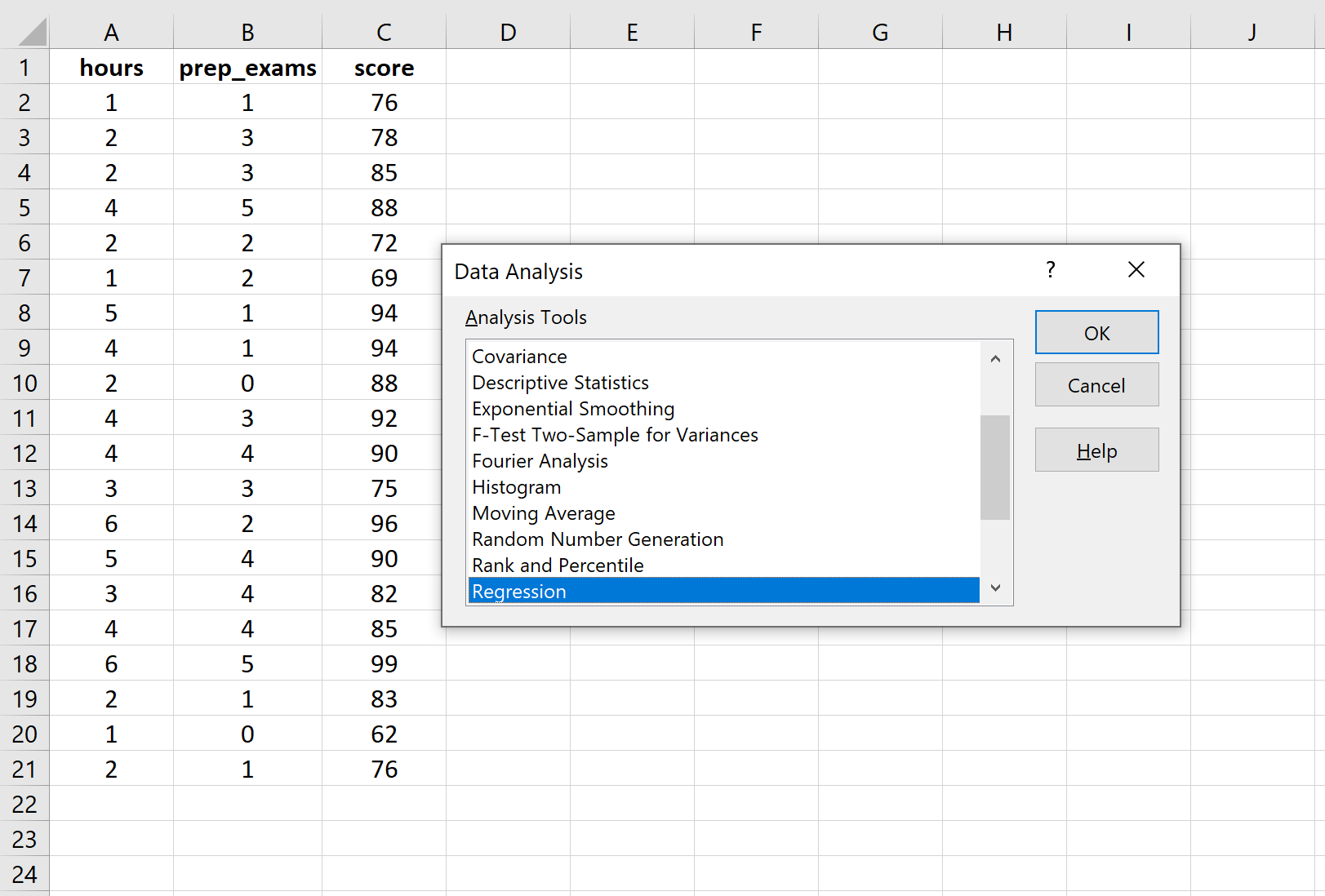
สำหรับ Input Y Range ให้กรอกอาร์เรย์ของค่าสำหรับตัวแปรตอบสนอง สำหรับ Input X Range ให้กรอกอาร์เรย์ของค่าสำหรับตัวแปรอธิบายสองตัว ทำเครื่องหมายที่ช่องถัดจาก ป้ายกำกับ เพื่อแจ้งให้ Excel ทราบว่าเราได้รวมชื่อตัวแปรไว้ในช่วงอินพุตแล้ว สำหรับ Output Range ให้เลือกเซลล์ที่คุณต้องการให้เอาต์พุตการถดถอยปรากฏ จากนั้นคลิก ตกลง

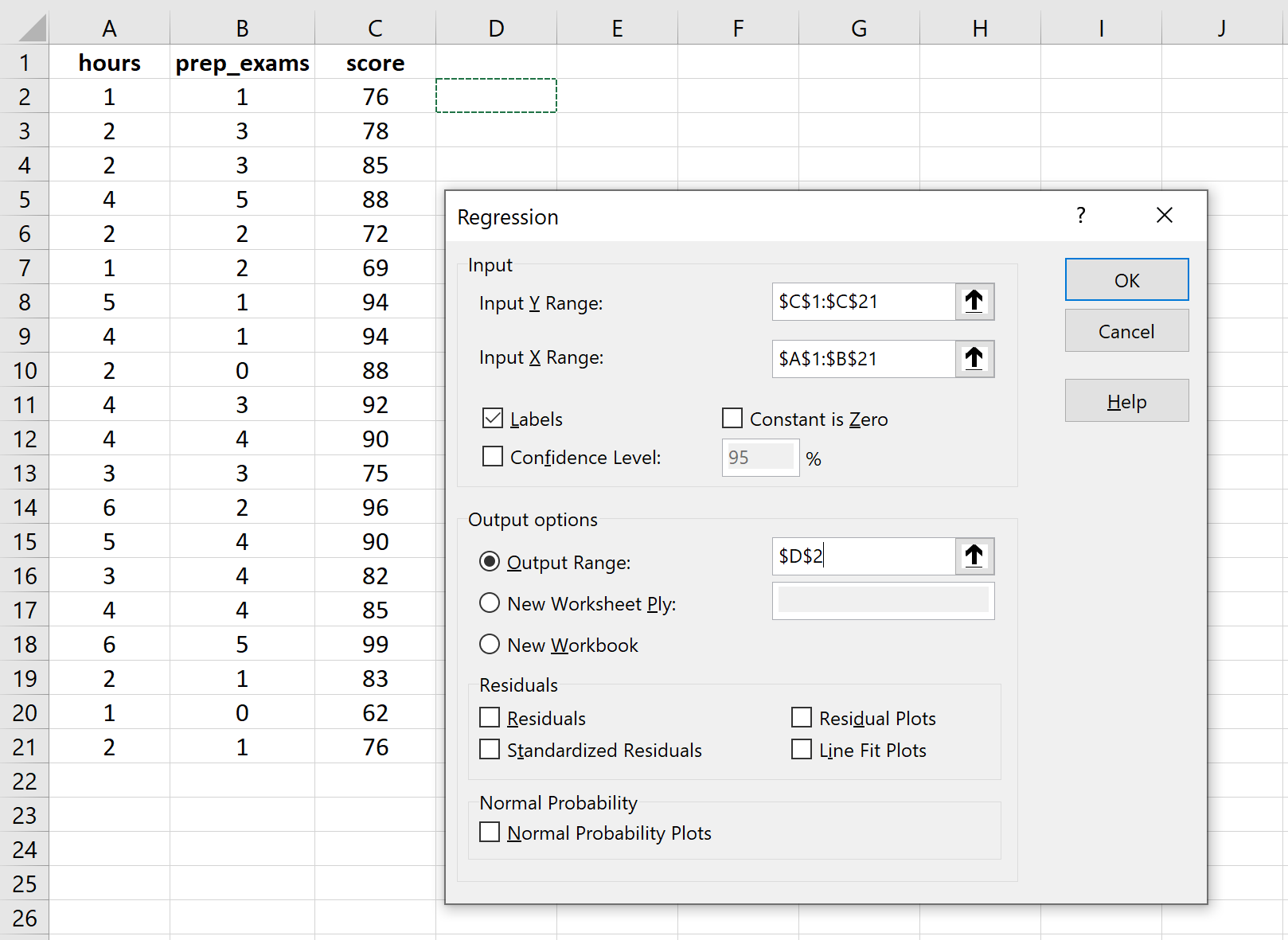
ผลลัพธ์ต่อไปนี้จะปรากฏขึ้นโดยอัตโนมัติ:

ขั้นตอนที่ 3: ตีความผลลัพธ์

ต่อไปนี้คือวิธีตีความตัวเลขที่เกี่ยวข้องมากที่สุดในผลลัพธ์:

อาร์ สแควร์: 0.734 . นี่เรียกว่าสัมประสิทธิ์การตัดสินใจ เป็นสัดส่วนของความแปรปรวนของตัวแปรตอบสนองที่สามารถอธิบายได้ด้วยตัวแปรอธิบาย ในตัวอย่างนี้ 73.4% ของการเปลี่ยนแปลงของคะแนนสอบอธิบายได้จากจำนวนชั่วโมงที่เรียนและจำนวนการสอบเพื่อเตรียมสอบ

ข้อผิดพลาดมาตรฐาน: 5.366 นี่คือระยะห่างเฉลี่ยระหว่างค่าที่สังเกตได้กับเส้นถดถอย ในตัวอย่างนี้ ค่าที่สังเกตได้เบี่ยงเบนไปจากเส้นถดถอยโดยเฉลี่ย 5,366 หน่วย

F: 23:46 น. นี่คือสถิติ F โดยรวมสำหรับแบบจำลองการถดถอย ซึ่งคำนวณเป็น MS การถดถอย/MS ที่เหลือ

ความหมาย F: 0.0000 นี่คือค่า p ที่เกี่ยวข้องกับสถิติ F โดยรวม ข้อมูลนี้บอกเราว่าแบบจำลองการถดถอยโดยรวมมีนัยสำคัญทางสถิติหรือไม่ กล่าวอีกนัยหนึ่ง มันบอกเราว่าตัวแปรอธิบายสองตัวที่รวมกันมีความสัมพันธ์ที่มีนัยสำคัญทางสถิติกับตัวแปรตอบสนองหรือไม่ ในกรณีนี้ ค่า p น้อยกว่า 0.05 ซึ่งบ่งชี้ว่าตัวแปรอธิบาย ชั่วโมงการศึกษา และ การสอบเตรียมสอบ รวมกัน มีความสัมพันธ์ที่มีนัยสำคัญทางสถิติกับ ผลการสอบ

ค่า P ค่า p ส่วนบุคคลบอกเราว่าตัวแปรอธิบายแต่ละตัวมีนัยสำคัญทางสถิติหรือไม่ เราจะเห็นว่า จำนวนชั่วโมงที่เรียน มีนัยสำคัญทางสถิติ (p = 0.00) ในขณะที่ การสอบเพื่อเตรียมการ (p = 0.52) ไม่มีนัยสำคัญทางสถิติที่ α = 0.05 เนื่องจาก การสอบเตรียมการที่ผ่านมา ไม่มีนัยสำคัญทางสถิติ เราจึงอาจตัดสินใจลบข้อสอบเหล่านั้นออกจากแบบจำลอง

ค่าสัมประสิทธิ์: ค่าสัมประสิทธิ์ของตัวแปรอธิบายแต่ละตัวบอกเราถึงการเปลี่ยนแปลงโดยเฉลี่ยที่คาดหวังในตัวแปรตอบสนอง โดยสมมติว่าตัวแปรอธิบายอื่น ๆ ยังคงที่ ตัวอย่างเช่น ในแต่ละชั่วโมงที่เรียนเพิ่มเติม คาดว่าคะแนนสอบเฉลี่ยจะเพิ่มขึ้น 5.56 โดยสมมติว่า ข้อสอบฝึกหัดที่เรียน คงที่

อีกวิธีในการดู: หากนักเรียน A และนักเรียน B ทำข้อสอบเตรียมสอบเท่ากัน แต่นักเรียน A เรียนนานกว่าหนึ่งชั่วโมง นักเรียน A ควรมีคะแนนสูงกว่านักเรียน B 5.56 คะแนน

เราตีความค่าสัมประสิทธิ์การสกัดกั้นว่าคะแนนสอบที่คาดหวังสำหรับนักเรียนที่ไม่ได้เรียนหลายชั่วโมงและไม่สอบเพื่อเตรียมการคือ 67.67

สมการการถดถอยโดยประมาณ: เราสามารถใช้สัมประสิทธิ์จากเอาต์พุตแบบจำลองเพื่อสร้างสมการการถดถอยโดยประมาณต่อไปนี้:

คะแนนสอบ = 67.67 + 5.56*(ชั่วโมง) – 0.60*(สอบเตรียมอุดมศึกษา)

เราสามารถใช้สมการการถดถอยโดยประมาณนี้เพื่อคำนวณคะแนนสอบที่คาดหวังสำหรับนักเรียน โดยพิจารณาจากจำนวนชั่วโมงเรียนและจำนวนข้อสอบฝึกหัดที่พวกเขาทำ เช่น นักเรียนที่เรียน 3 ชั่วโมงและสอบเตรียมสอบควรได้เกรด 83.75 :

คะแนนสอบ = 67.67 + 5.56*(3) – 0.60*(1) = 83.75

โปรดทราบว่าเนื่องจาก การสอบเตรียมการที่ผ่านมา ไม่มีนัยสำคัญทางสถิติ (p=0.52) เราอาจตัดสินใจลบออกเนื่องจากไม่ได้ให้การปรับปรุงใดๆ กับโมเดลโดยรวม ในกรณีนี้ เราสามารถทำการถดถอยเชิงเส้นอย่างง่ายโดยใช้เพียง ชั่วโมงที่ศึกษา เป็นตัวแปรอธิบาย

สามารถดูผลลัพธ์ของการวิเคราะห์การถดถอยเชิงเส้นอย่างง่ายได้ ที่นี่

แหล่งข้อมูลเพิ่มเติม

เมื่อคุณดำเนินการถดถอยเชิงเส้นหลายครั้งแล้ว คุณอาจต้องการตรวจสอบสมมติฐานหลายประการ ได้แก่:

1. การทดสอบ multicollinearity โดยใช้ VIF

2. ทดสอบหาความต่างศักย์ไฟฟ้าโดยใช้การทดสอบ Breusch-Pagan

3. ทดสอบความเป็นปกติโดยใช้พล็อต QQ