รู้เบื้องต้นเกี่ยวกับการถดถอยโลจิสติก
เมื่อเราต้องการเข้าใจความสัมพันธ์ระหว่างตัวแปรทำนายตั้งแต่หนึ่งตัวขึ้นไปกับตัวแปรตอบสนองต่อเนื่อง เรามักจะใช้ การถดถอยเชิงเส้น
อย่างไรก็ตาม เมื่อตัวแปรตอบสนองเป็นแบบหมวดหมู่ เราสามารถใช้ การถดถอยโลจิสติก ได้
การถดถอยโลจิสติกเป็นประเภทของอัลก อริธึมการจำแนก ประเภทเนื่องจากพยายาม “จัดประเภท” การสังเกตในชุดข้อมูลออกเป็นหมวดหมู่ที่แตกต่างกัน
นี่คือตัวอย่างบางส่วนของการใช้การถดถอยโลจิสติก:
- เราต้องการใช้ คะแนนเครดิต และ ยอดคงเหลือในธนาคาร เพื่อคาดการณ์ว่าลูกค้ารายนั้นจะผิดนัดชำระหนี้หรือไม่ (ตัวแปรการตอบสนอง = “ค่าเริ่มต้น” หรือ “ไม่มีค่าเริ่มต้น”)
- เราต้องการใช้ การรีบาวด์เฉลี่ยต่อเกม และ คะแนนเฉลี่ยต่อเกม เพื่อคาดการณ์ว่าผู้เล่นบาสเก็ตบอลคนใดคนหนึ่งจะถูกดราฟท์เข้าสู่ NBA หรือไม่ (ตัวแปรการตอบสนอง = “ดราฟต์” หรือ “ไม่ได้ดราฟต์”)
- เราต้องการใช้ พื้นที่เป็นตารางฟุต และ จำนวนห้องน้ำ เพื่อคาดการณ์ว่าบ้านในเมืองหนึ่งๆ จะแสดงในราคาขาย 200,000 ดอลลาร์ขึ้นไปหรือไม่ (ตัวแปรการตอบสนอง = “ใช่” หรือ “ไม่ใช่”)
โปรดทราบว่าตัวแปรการตอบสนองในแต่ละตัวอย่างเหล่านี้สามารถรับได้เพียงค่าใดค่าหนึ่งจากสองค่าเท่านั้น เปรียบเทียบสิ่งนี้กับการถดถอยเชิงเส้นซึ่งตัวแปรตอบสนองรับค่าต่อเนื่อง
สมการถดถอยโลจิสติก
การถดถอยโลจิสติกใช้วิธีการที่เรียกว่าการประมาณค่าความน่าจะเป็นสูงสุด (รายละเอียดจะไม่กล่าวถึงในที่นี้) เพื่อค้นหาสมการในรูปแบบต่อไปนี้:
บันทึก[p(X) / ( 1 -p(X))] = β 0 + β 1 X 1 + β 2 X 2 + … + β พี
ทอง:
- X j : ตัวแปร ทำนายที่ j
- β j : การประมาณค่าสัมประสิทธิ์ของตัวแปรทำนายที่ j
สูตรทางด้านขวาของสมการทำนาย อัตราต่อรองของบันทึก ที่ตัวแปรตอบกลับรับค่า 1
ดังนั้น เมื่อเราปรับแบบจำลองการถดถอยลอจิสติกให้เหมาะสม เราสามารถใช้สมการต่อไปนี้เพื่อคำนวณความน่าจะเป็นที่การสังเกตที่กำหนดจะได้ค่า 1:
p(X) = อี β 0 + β 1 X 1 + β 2 X 2 + … + β p
จากนั้นเราใช้เกณฑ์ความน่าจะเป็นที่แน่นอนเพื่อจัดประเภทการสังเกตเป็น 1 หรือ 0
ตัวอย่างเช่น เราสามารถพูดได้ว่าการสังเกตที่มีความน่าจะเป็นมากกว่าหรือเท่ากับ 0.5 จะถูกจัดประเภทเป็น “1” และการสังเกตอื่นๆ ทั้งหมดจะถูกจัดประเภทเป็น “0”
วิธีการตีความผลลัพธ์ของการถดถอยโลจิสติก
สมมติว่าเราใช้แบบจำลองการถดถอยลอจิสติกส์เพื่อคาดการณ์ว่าผู้เล่นบาสเกตบอลคนใดคนหนึ่งจะถูกร่างเข้าสู่ NBA หรือไม่ โดยพิจารณาจากค่าเฉลี่ยการรีบาวด์ต่อเกมและคะแนนเฉลี่ยต่อเกม
นี่คือผลลัพธ์ของแบบจำลองการถดถอยโลจิสติก:
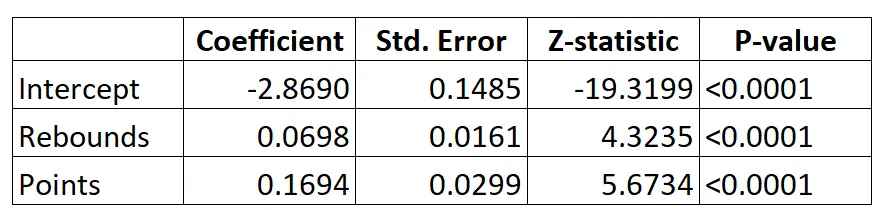
เมื่อใช้ค่าสัมประสิทธิ์ เราสามารถคำนวณความน่าจะเป็นของผู้เล่นที่กำหนดเข้าสู่ NBA โดยพิจารณาจากการรีบาวด์และคะแนนเฉลี่ยต่อเกมโดยใช้สูตรต่อไปนี้:
P(ดราฟท์) = e -2.8690 + 0.0698*(รีบส์) + 0.1694*(พอยท์) / (1+e -2.8690 + 0.0698*(รีบส์) + 0.1694*(พอยท์) ) )
ตัวอย่างเช่น สมมติว่าผู้เล่นคนหนึ่งโดยเฉลี่ย 8 รีบาวน์ต่อเกมและ 15 แต้มต่อเกม ตามแบบจำลอง ความน่าจะเป็นที่ผู้เล่นคนนี้จะถูกร่างเข้าสู่ NBA คือ 0.557
P(เขียน) = e -2.8690 + 0.0698*(8) + 0.1694*(15) / (1+e -2.8690 + 0.0698*(8) + 0.1694*(15 ) ) = 0.557
เนื่องจากความน่าจะเป็นนี้มากกว่า 0.5 เราจึงคาดการณ์ว่าผู้เล่นรายนี้จะถูกดราฟต์
เปรียบเทียบกับผู้เล่นที่เฉลี่ยเพียง 3 รีบาวน์และ 7 แต้มต่อเกม ความน่าจะเป็นที่ผู้เล่นคนนี้จะถูกร่างเข้าสู่ NBA คือ 0.186
P(เขียน) = e -2.8690 + 0.0698*(3) + 0.1694*(7) / (1+e -2.8690 + 0.0698*(3) + 0.1694*(7 ) ) = 0.186
เนื่องจากความน่าจะเป็นนี้น้อยกว่า 0.5 เราจึงคาดการณ์ว่าผู้เล่นรายนี้จะไม่ถูกดราฟต์
สมมติฐานการถดถอยโลจิสติก
การถดถอยโลจิสติกใช้สมมติฐานต่อไปนี้:
1. ตัวแปรตอบสนองเป็นไบนารี สันนิษฐานว่าตัวแปรตอบสนองสามารถรับผลลัพธ์ที่เป็นไปได้เพียงสองรายการเท่านั้น
2. การสังเกตมีความเป็นอิสระ สันนิษฐานว่าการสังเกตในชุดข้อมูลมีความเป็นอิสระจากกัน กล่าวคือ การสังเกตไม่ควรมาจากการวัดซ้ำของบุคคลคนเดียวกันหรือเกี่ยวข้องกันในทางใดทางหนึ่ง
3. ไม่มีความหลากหลายที่ร้ายแรงระหว่างตัวแปรทำนาย สันนิษฐานว่าไม่มีตัวแปรทำนายใดมี ความสัมพันธ์กันสูง
4. ไม่มีค่าผิดปกติที่รุนแรง สันนิษฐานว่าไม่มีค่าผิดปกติหรือข้อสังเกตที่มีอิทธิพลในชุดข้อมูล
5. มีความสัมพันธ์เชิงเส้นตรงระหว่างตัวแปรทำนายและบันทึกของตัวแปรตอบสนอง สมมติฐานนี้สามารถทดสอบได้โดยใช้การทดสอบ Box-Tidwell
6. ขนาดตัวอย่างมีขนาดใหญ่เพียงพอ โดยทั่วไป คุณควรมีกรณีอย่างน้อย 10 กรณีโดยให้ผลลัพธ์ที่เกิดขึ้นน้อยที่สุดสำหรับตัวแปรอธิบายแต่ละตัว ตัวอย่างเช่น หากคุณมีตัวแปรอธิบาย 3 ตัว และความน่าจะเป็นที่คาดหวังของผลลัพธ์ที่เกิดบ่อยน้อยที่สุดคือ 0.20 คุณควรมีขนาดตัวอย่างอย่างน้อย (10*3) / 0.20 = 150
ลองอ่าน บทความนี้ เพื่อดูคำอธิบายโดยละเอียดเกี่ยวกับวิธีการตรวจสอบสมมติฐานเหล่านี้