วิธีทดสอบความสำคัญของความชันการถดถอย

สมมติว่าเรามีชุดข้อมูลต่อไปนี้ซึ่งแสดงพื้นที่เป็นตารางฟุตและราคาของบ้าน 12 หลังที่แตกต่างกัน:

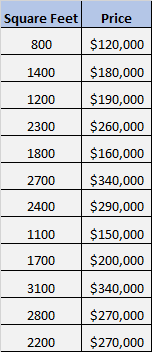
เราต้องการทราบว่ามีความสัมพันธ์ที่สำคัญระหว่างพื้นที่เป็นตารางฟุตและราคาหรือไม่

เพื่อให้เข้าใจว่าข้อมูลมีลักษณะอย่างไร ขั้นแรกเราจะสร้างแผนภาพกระจายที่มี ตารางฟุต บนแกน x และ ราคา บนแกน y:

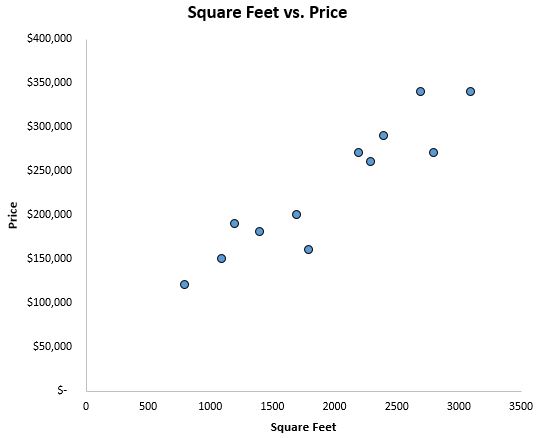
เราจะเห็นได้อย่างชัดเจนว่ามีความสัมพันธ์เชิงบวกระหว่างพื้นที่เป็นตารางฟุตและราคา เมื่อพื้นที่เป็นตารางฟุตเพิ่มขึ้น ราคาบ้านก็มีแนวโน้มเพิ่มขึ้นเช่นกัน

อย่างไรก็ตาม หากต้องการทราบว่ามี ความสัมพันธ์ ที่มีนัยสำคัญทางสถิติ ระหว่างพื้นที่เป็นตารางฟุตและราคาหรือไม่ เราจำเป็นต้องเรียกใช้การถดถอยเชิงเส้นอย่างง่าย

ดังนั้นเราจึงใช้ การถดถอยเชิงเส้นอย่างง่าย โดยใช้ ตารางฟุต เป็นตัวทำนายและ ราคาเป็นการ ตอบสนอง และได้ผลลัพธ์ดังต่อไปนี้:

ไม่ว่าคุณจะรันการถดถอยเชิงเส้นอย่างง่ายใน Excel, SPSS, R หรือซอฟต์แวร์อื่นๆ คุณจะได้ผลลัพธ์ที่คล้ายกับที่แสดงด้านบน

โปรดจำไว้ว่าการถดถอยเชิงเส้นอย่างง่ายจะสร้างเส้นที่เหมาะสมที่สุด ซึ่งเป็นสมการของเส้นที่ “พอดี” กับข้อมูลในแผนภาพกระจายของเรามากที่สุด เส้นที่เหมาะสมที่สุดนี้ถูกกำหนดเป็น:

ŷ = ข ₀ + ข ₁ x

โดยที่ ŷ คือค่าทำนายของตัวแปรตอบสนอง b ₀ คือจุดตัด b ₁ คือสัมประสิทธิ์การถดถอย และ x คือค่าของตัวแปรทำนาย

ค่าของ b ₀ กำหนดโดยสัมประสิทธิ์ของแหล่งกำเนิดซึ่งก็คือ 47588.70

ค่าของ b ₁ กำหนดโดยสัมประสิทธิ์ของตัวแปรทำนาย Square Feet ซึ่งก็คือ 93.57

ดังนั้น เส้นตรงที่เหมาะสมที่สุดในตัวอย่างนี้คือ ŷ = 47588.70+ 93.57x

วิธีตีความบรรทัดที่เหมาะที่สุดนี้:

• b ₀ : เมื่อค่าตารางฟุตเป็นศูนย์ มูลค่าราคาเฉลี่ยที่คาดหวังคือ 47,588.70 ดอลลาร์ (ในกรณีนี้ การตีความค่าตัดขวางนั้นไม่สมเหตุสมผล เนื่องจากบ้านไม่มีพื้นที่เป็นศูนย์ตารางฟุตได้)
• b ₁ : สำหรับแต่ละตารางฟุตเพิ่มเติม ราคาเฉลี่ยที่คาดว่าจะเพิ่มขึ้นคือ 93.57 ดอลลาร์

ตอนนี้เรารู้แล้วว่าราคาที่เพิ่มขึ้นโดยเฉลี่ยที่คาดหวังคือ 93.57 ดอลลาร์ต่อตารางฟุตที่เพิ่มขึ้นแต่ละตารางฟุต

หากต้องการทราบว่าการเพิ่มขึ้นนี้มีนัยสำคัญทางสถิติหรือไม่ เราจำเป็นต้องทำการทดสอบสมมติฐานสำหรับ B ₁ หรือสร้างช่วงความเชื่อมั่นสำหรับ B ₁

หมายเหตุ : การทดสอบสมมติฐานและช่วงความเชื่อมั่นจะให้ผลลัพธ์ที่เหมือนกันเสมอ

การสร้างช่วงความเชื่อมั่นสำหรับความชันการถดถอย

ในการสร้างช่วงความเชื่อมั่นสำหรับความชันการถดถอย เราใช้สูตรต่อไปนี้:

ช่วงความเชื่อมั่น = b ₁ +/- (t _{1-∝/2, n-2} ) * (ข้อผิดพลาดมาตรฐานของ b ₁ )

ทอง:

• b ₁ คือค่าสัมประสิทธิ์ความชันที่กำหนดในผลการถดถอย
• (t _{1-∝/2, n-2} ) คือค่า t วิกฤตสำหรับระดับความเชื่อมั่น 1-∝ โดยมีดีกรีอิสระ n-2 โดยที่ n คือจำนวนการสังเกตทั้งหมดในชุดข้อมูลของเรา
• (ข้อผิดพลาดมาตรฐานของ b ₁ ) คือข้อผิดพลาดมาตรฐานของ b ₁ ที่กำหนดในผลลัพธ์การถดถอย

สำหรับตัวอย่างของเรา ต่อไปนี้เป็นวิธีสร้างช่วงความเชื่อมั่น 95% สำหรับ B ₁ :

• b ₁ คือ 93.57 จากเอาต์พุตการถดถอย
• เนื่องจากเราใช้ช่วงความเชื่อมั่น 95% ∝ = 0.05 และ n-2 = 12-2 = 10 ดังนั้น t _{0.975, 10} คือ 2.228 ตามตารางการกระจาย t
• (ข้อผิดพลาดมาตรฐานของ _b1 ) คือ 11.45 จากเอาต์พุตการถดถอย

ดังนั้น ช่วงความมั่นใจ 95% ของเราสำหรับ B ₁ คือ:

93.57 +/- (2.228) * (11.45) = (68.06, 119.08)

ซึ่งหมายความว่าเรามั่นใจ 95% ว่าราคาเฉลี่ยที่เพิ่มขึ้นจริงสำหรับแต่ละตารางฟุตเพิ่มเติมจะอยู่ระหว่าง 68.06 ถึง 119.08 ดอลลาร์

โปรดทราบว่า $0 ไม่ได้อยู่ในช่วงนี้ ดังนั้นความสัมพันธ์ระหว่างพื้นที่เป็นตารางฟุตและราคาจึงมีนัยสำคัญทางสถิติที่ระดับความเชื่อมั่น 95%

ทำการทดสอบสมมติฐานสำหรับความชันการถดถอย

ในการทำการทดสอบสมมติฐานสำหรับความชันการถดถอย เราจะปฏิบัติตาม ขั้นตอนมาตรฐาน 5 ขั้นตอนสำหรับการทดสอบสมมติฐานใดๆ :

ขั้นตอนที่ 1 ระบุสมมติฐาน

สมมติฐานว่าง (H0): B ₁ = 0

สมมติฐานทางเลือก: (ฮา): B ₁ ≠ 0

ขั้นตอนที่ 2 กำหนดระดับนัยสำคัญที่จะใช้

เนื่องจากเราสร้างช่วงความเชื่อมั่น 95% ในตัวอย่างก่อนหน้านี้ เราจะใช้แนวทางที่เทียบเท่าที่นี่และเลือกใช้ระดับนัยสำคัญที่ 0.05

ขั้นตอนที่ 3 ค้นหาสถิติการทดสอบและค่า p ที่สอดคล้องกัน

ในกรณีนี้ สถิติการทดสอบคือ t = สัมประสิทธิ์ของ b ₁ / ค่าคลาดเคลื่อนมาตรฐานของ b ₁ โดยมีดีกรีอิสระ n-2 เราสามารถหาค่าเหล่านี้ได้จากผลการถดถอย:

ดังนั้นสถิติการทดสอบ t = 92.89 / 13.88 = 6.69

การใช้ เครื่องคำนวณคะแนน T ถึงค่า P ด้วยคะแนน 6.69 พร้อมความอิสระ 10 องศาและการทดสอบแบบสองด้าน ค่า p = 0.000

ขั้นตอนที่ 4 ปฏิเสธหรือไม่ปฏิเสธสมมติฐานว่าง

เนื่องจากค่า p ต่ำกว่าระดับนัยสำคัญของเราที่ 0.05 เราจึงปฏิเสธสมมติฐานว่าง

ขั้นตอนที่ 5 ตีความผลลัพธ์

เนื่องจากเราปฏิเสธสมมติฐานว่าง เรามีหลักฐานเพียงพอที่จะบอกว่าราคาที่เพิ่มขึ้นโดยเฉลี่ยที่แท้จริงสำหรับแต่ละตารางฟุตเพิ่มเติมนั้นไม่เป็นศูนย์