การทดสอบพหุนามคืออะไร? (คำจำกัดความ & #038; ตัวอย่าง)
การทดสอบพหุนาม ใช้เพื่อพิจารณาว่าตัวแปรเชิงหมวดหมู่เป็นไปตามการแจกแจงเชิงสมมุติหรือไม่
การทดสอบนี้ใช้ สมมติฐาน ว่างและทางเลือกต่อไปนี้:
H 0 : ตัวแปรเด็ดขาดตามการแจกแจงสมมุติฐาน
H A : ตัวแปรเชิงหมวดหมู่ ไม่เป็นไปตาม การแจกแจงเชิงสมมุติ
หาก ค่า p ของการทดสอบต่ำกว่าระดับนัยสำคัญที่กำหนด (เช่น α = 0.05) เราก็สามารถปฏิเสธสมมติฐานว่างและสรุปได้ว่าตัวแปรไม่เป็นไปตามการแจกแจงตามสมมติฐาน
การทดสอบนี้ใช้เมื่อตัวแปรสามารถรับผลลัพธ์ที่แตกต่างกัน k รายการ ตัวอย่างคลาสสิกของการทดสอบพหุนามคือจุดที่เราต้องการตรวจสอบว่าลูกเต๋าบางลูกนั้นยุติธรรมหรือไม่ เมื่อคุณทอยลูกเต๋า ความน่าจะเป็นที่จะตกในแต่ละหมายเลข (1 ถึง 6) คือ 1/6
เพื่อทดสอบว่าลูกเต๋านั้นยุติธรรมหรือไม่ เราอาจทอยมันหลายครั้งและดูว่าจำนวนครั้งที่มันตกลงบนตัวเลขที่แตกต่างกันนั้นแตกต่างอย่างมากจากที่เราคาดหวังหรือไม่
ตัวอย่างต่อไปนี้แสดงวิธีดำเนินการทดสอบพหุนามโดยใช้ภาษาการเขียนโปรแกรมเชิงสถิติ R
ตัวอย่างที่ 1: ลูกเต๋ายุติธรรม
สมมติว่าเราต้องการพิจารณาว่าการตายนั้นยุติธรรมหรือไม่ เพื่อทดสอบสิ่งนี้ เราดำเนินการ 30 ครั้งและบันทึกความถี่ของผลลัพธ์แต่ละรายการ ตารางต่อไปนี้แสดงผลลัพธ์:
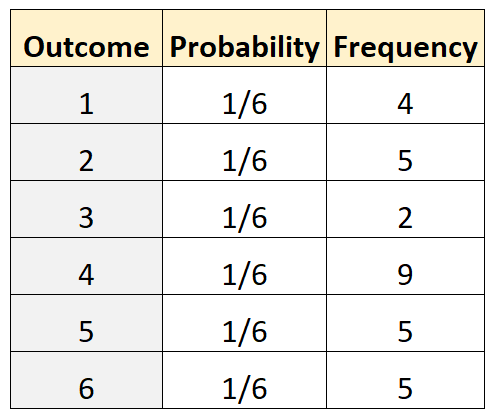
รหัสต่อไปนี้ใน R สามารถใช้เพื่อทำการทดสอบพหุนาม:
library (EMT)
#specify probability of each outcome
prob <- c(1/6, 1/6, 1/6, 1/6, 1/6, 1/6)
#specify frequency of each outcome from experiment
actual <- c(4, 5, 2, 9, 5, 5)
#perform multinomial test
multinomial. test (actual, prob)
Exact Multinomial Test, distance measure: p
Events pObs p.value
324632 0 0.4306
ค่า p ของการทดสอบคือ 0.4306 เนื่องจากค่า p นี้ไม่น้อยกว่า 0.05 เราจึงไม่ปฏิเสธสมมติฐานว่าง ดังนั้นเราจึงไม่มีหลักฐานเพียงพอที่จะบอกว่าลูกเต๋าไม่ยุติธรรม
ตัวอย่างที่ 2: การขายสินค้า
สมมติว่าเจ้าของร้านค้าตั้งสมมติฐานว่าลูกค้าจำนวนเท่ากันจะซื้อผลิตภัณฑ์แต่ละอย่างจากสี่ผลิตภัณฑ์ที่แตกต่างกัน เพื่อทดสอบสิ่งนี้ ระบบจะบันทึกจำนวนลูกค้าที่ซื้อผลิตภัณฑ์แต่ละรายการในสัปดาห์ที่กำหนด ตารางต่อไปนี้แสดงผลลัพธ์:
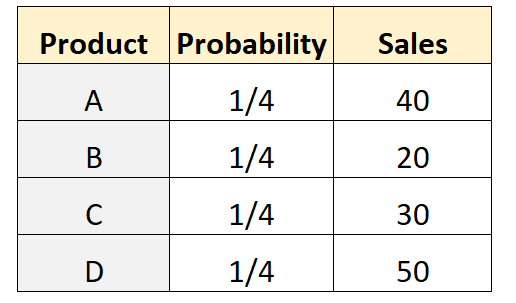
รหัสต่อไปนี้ใน R สามารถใช้เพื่อทำการทดสอบพหุนามบนชุดข้อมูลนี้:
library (EMT)
#specify probability of each outcome
prob <- c(1/4, 1/4, 1/4, 1/4)
#specify frequency of each outcome from experiment
actual <- c(40, 20, 30, 50)
#perform multinomial test
multinomial. test (actual, prob)
Exact Multinomial Test, distance measure: p
Events pObs p.value
477191 0 0.00226
ค่า p ของการทดสอบคือ 0.00226 เนื่องจากค่า p นี้น้อยกว่า 0.05 เราจะปฏิเสธสมมติฐานว่าง เราจึงมีหลักฐานเพียงพอที่จะบอกว่ายอดขายแต่ละสินค้าไม่เท่ากัน
ตัวอย่างที่ 3: ลูกหินในถุง
ทอมระบุว่าความน่าจะเป็นในการเลือกหินอ่อนสีแดง เขียว หรือม่วงจากถุงคือ 0.2, 0.5 และ 0.3 ตามลำดับ เพื่อทดสอบสิ่งนี้ ไมค์ เพื่อนของเขาล้วงเข้าไปในถุงแล้วดึงหินอ่อนออกมา (พร้อมชิ้นส่วนทดแทน) 100 ครั้งที่แตกต่างกัน ตารางต่อไปนี้แสดงผลลัพธ์:
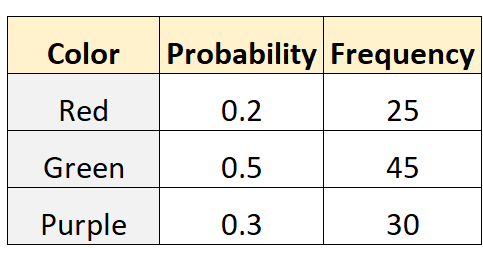
รหัสต่อไปนี้ใน R สามารถใช้เพื่อทำการทดสอบพหุนามบนชุดข้อมูลนี้:
library (EMT)
#specify probability of each outcome
prob <- c(.2, .5, .3)
#specify frequency of each outcome from experiment
actual <- c(40, 20, 30, 50)
#perform multinomial test
multinomial. test (actual, prob)
Exact Multinomial Test, distance measure: p
Events pObs p.value
5151 0.0037 0.3999
ค่า p ของการทดสอบคือ 0.3999 เนื่องจากค่า p นี้ไม่น้อยกว่า 0.05 เราจึงไม่สามารถปฏิเสธสมมติฐานว่างได้ เราจึงไม่มีหลักฐานเพียงพอที่จะบอกว่าการกระจายลูกแก้วในถุงแตกต่างจากที่ทอมระบุ
แหล่งข้อมูลเพิ่มเติม
ความรู้เบื้องต้นเกี่ยวกับการแจกแจงพหุนาม
เครื่องคำนวณการกระจายพหุนาม