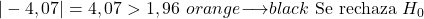การทดสอบสมมติฐานเพื่อหาสัดส่วน

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 3, 2023 สถิติ 0 ความคิดเห็น

บทความนี้จะอธิบายว่าการทดสอบสมมติฐานสัดส่วนในสถิติคืออะไร ดังนั้นคุณจะพบสูตรสำหรับการทดสอบสมมติฐานสำหรับสัดส่วน และยังมีแบบฝึกหัดทีละขั้นตอนเพื่อให้เข้าใจอย่างถ่องแท้ว่าทำได้อย่างไร

การทดสอบสมมติฐานเพื่อสัดส่วนคืออะไร?

การทดสอบสมมติฐานเชิงสัดส่วน เป็นวิธีการทางสถิติที่ใช้ในการพิจารณาว่าจะปฏิเสธสมมติฐานว่างของสัดส่วนประชากรหรือไม่

ดังนั้น ขึ้นอยู่กับค่าของสถิติการทดสอบสมมติฐานสำหรับสัดส่วนและระดับนัยสำคัญ สมมติฐานว่างจึงถูกปฏิเสธหรือยอมรับ

โปรดทราบว่าการทดสอบสมมติฐานอาจเรียกอีกอย่างว่าความแตกต่างของสมมติฐาน การทดสอบสมมติฐาน หรือการทดสอบนัยสำคัญ

สูตรทดสอบสมมุติฐานสำหรับสัดส่วน

สถิติการทดสอบสมมติฐานสำหรับสัดส่วนจะเท่ากับผลต่างในสัดส่วนตัวอย่างลบด้วยค่าที่เสนอของสัดส่วนหารด้วยค่าเบี่ยงเบนมาตรฐานของสัดส่วน

สูตรสมมติฐานการทดสอบสัดส่วน จึงเป็นดังนี้

$\displaystyle Z=\frac{\widehat{p}-p}{\displaystyle\sqrt{\frac{p(1-p)}{n}}}$

ทอง:

$Z$

คือสถิติการทดสอบสมมติฐานสำหรับสัดส่วน
$\widehat{p}$

คือสัดส่วนตัวอย่าง
$p$

คือมูลค่าตามสัดส่วนที่เสนอ
$n$

คือขนาดตัวอย่าง
$\displaystyle\sqrt{\frac{p(1-p)}{n}}$

คือค่าเบี่ยงเบนมาตรฐานของสัดส่วน

โปรดทราบว่าการคำนวณสถิติการทดสอบสมมติฐานสำหรับสัดส่วนนั้นไม่เพียงพอ แต่ผลลัพธ์จะต้องถูกตีความ:

หากการทดสอบสมมติฐานสำหรับสัดส่วนเป็นแบบสองด้าน สมมติฐานว่างจะถูกปฏิเสธหากค่าสัมบูรณ์ของสถิติมากกว่าค่าวิกฤต Z _α/2
หากการทดสอบสมมติฐานสำหรับสัดส่วนตรงกับส่วนหางด้านขวา สมมติฐานว่างจะถูกปฏิเสธหากสถิติมากกว่าค่าวิกฤต Z _α
หากการทดสอบสมมติฐานสำหรับสัดส่วนตรงกับหางซ้าย สมมติฐานว่างจะถูกปฏิเสธหากสถิติน้อยกว่าค่าวิกฤต -Z _α

$\begin{array}{l}H_1: p\neq p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |Z|>Z_{\alpha/2} \text{ se rechaza } H_0\\[3ex]H_1: p> p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z>Z_{\alpha} \text{ se rechaza } H_0\\[3ex]H_1: p< p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z<-Z_{\alpha} \text{ se rechaza } H_0\end{array}$

โปรดจำไว้ว่าสามารถรับค่าวิกฤตได้อย่างง่ายดายจากตารางการแจกแจงแบบปกติ

➤ ดูที่: ตารางการแจกแจงแบบปกติ

ตัวอย่างการทดสอบสมมติฐานสำหรับสัดส่วน

เมื่อเราเห็นคำจำกัดความของการทดสอบสมมติฐานเรื่องสัดส่วนแล้วสูตรของมันคืออะไร เราก็จะแก้ตัวอย่างเพื่อทำความเข้าใจแนวคิดได้ดีขึ้น

ตามที่ผู้ผลิตระบุว่ายารักษาโรคเฉพาะนั้นมีประสิทธิภาพ 70% ในห้องปฏิบัติการ เราทดสอบประสิทธิผลของยานี้เนื่องจากนักวิจัยเชื่อว่าสัดส่วนแตกต่างกัน สำหรับสิ่งนี้ ยานี้ได้รับการทดสอบกับกลุ่มตัวอย่างผู้ป่วย 1,000 ราย และผู้ป่วย 641 รายที่ได้รับการรักษาจนหายขาด ทำการทดสอบสมมติฐานกับสัดส่วนประชากรด้วยระดับนัยสำคัญ 5% เพื่อปฏิเสธหรือไม่ยอมรับสมมติฐานของผู้วิจัย

ในกรณีนี้ สมมติฐานว่างและสมมติฐานทางเลือก ของการทดสอบสมมติฐานสำหรับสัดส่วนประชากรคือ:

$\begin{cases}H_0: p=0,70\\[2ex] H_1:p\neq 0,70 \end{cases}$

สัดส่วนของกลุ่มตัวอย่างที่ได้รับการรักษาด้วยยาคือ

$\widehat{p}=\cfrac{641}{1000}=0,641$

เราคำนวณสถิติการทดสอบสมมติฐานสำหรับสัดส่วนโดยใช้สูตรที่เห็นด้านบน:

$\begin{aligned} \displaystyle Z&=\frac{\widehat{p}-p}{\displaystyle\sqrt{\frac{p(1-p)}{n}}}\\[2ex]Z&=\frac{0,641-0,70}{\displaystyle\sqrt{\frac{0,70\cdot (1-0,70)}{1000}}} \\[2ex] Z&=-4,07\end{aligned}}$

ในทางกลับกัน เนื่องจากระดับนัยสำคัญคือ 0.05 และนี่คือการทดสอบสมมติฐานแบบสองด้าน ค่าวิกฤตของการทดสอบคือ 1.96

$Z_{0,025}=1,96$

➤ ดู: ระดับนัยสำคัญ 0.05

โดยสรุป ค่าสัมบูรณ์ของสถิติการทดสอบมากกว่าค่าวิกฤต ดังนั้นเราจึงปฏิเสธสมมติฐานว่างและยอมรับสมมติฐานทางเลือก

$|-4,07|=4,07>1,96 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Se rechaza } H_0″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”424″ style=”vertical-align: -5px;”></p> </p> <div style=$ ➤ ดู: การทดสอบสมมุติฐานสำหรับค่าเฉลี่ย

การทดสอบสมมติฐานสำหรับสัดส่วนตัวอย่างสองสัดส่วน

การทดสอบสมมติฐานสำหรับสัดส่วนของสองตัวอย่าง ใช้เพื่อปฏิเสธหรือยอมรับสมมติฐานว่างที่ว่าสัดส่วนของประชากรสองกลุ่มเท่ากัน

ดังนั้น สมมติฐานว่างของการทดสอบสมมติฐานสำหรับสัดส่วนสองตัวอย่างจะเป็นดังนี้เสมอ

$H_0: p_1=p_2$

ในขณะที่สมมติฐานทางเลือกสามารถเป็นหนึ่งในสามตัวเลือก:

 *** QuickLaTeX cannot compile formula:
\begin{array}{l}H_1:p_1\neq p_2\\[2ex]H_1:p_1>p_2\\[2ex]H_1:p_1 The combined ratio of the two samples is calculated as follows:[latex]p=\cfrac {x_1+x_2}{n_1+n_2}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{l}
Please use \mathaccent for accents in math mode.
leading text: ...H_1:p_1>p_2\\[2ex]H_1:p_1 The combined ratio
Please use \mathaccent for accents in math mode.
leading text: ...\[2ex]H_1:p_1 The combined ratio of the two
Please use \mathaccent for accents in math mode.
leading text: ...combined of the two samples is calculated
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.

และสูตรคำนวณสถิติการทดสอบสมมติฐานสำหรับสัดส่วนตัวอย่างสองสัดส่วนคือ

$\displaystyle Z=\frac{\displaystyle \frac{x_1}{n_1}-\frac{x_2}{n_2}}{\displaystyle \sqrt{p(1-p)\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}}$

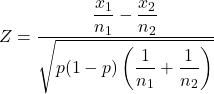
ทอง:

$Z$

คือสถิติการทดสอบสมมติฐานสำหรับสัดส่วนสองตัวอย่าง
$x_1$

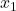
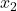
คือจำนวนผลลัพธ์ในตัวอย่างที่ 1
$x_2$

คือจำนวนผลลัพธ์ในตัวอย่างที่ 2
$n_1$

คือขนาดตัวอย่างที่ 1
$n_2$

คือขนาดตัวอย่างที่ 2
$p$

คือสัดส่วนรวมของทั้งสองตัวอย่าง

การทดสอบสมมติฐานสำหรับสัดส่วนตัวอย่าง k

ใน การทดสอบสมมติฐานเกี่ยวกับสัดส่วนของกลุ่มตัวอย่าง k เป้าหมายคือเพื่อตรวจสอบว่าสัดส่วนทั้งหมดของประชากรที่แตกต่างกันเท่ากันหรือในทางกลับกัน ว่ามีสัดส่วนต่างกันหรือไม่ ดังนั้น สมมติฐานว่างและสมมติฐานทางเลือกในกรณีนี้คือ:

$\begin{cases}H_0: \text{Todas las proporciones son iguales}\\[2ex] H_1: \text{No todas las proporciones son iguales} \end{cases}$

ในกรณีนี้ สัดส่วนรวมของกลุ่มตัวอย่างทั้งหมดจะคำนวณดังนี้:

$p=\cfrac{\displaystyle\sum_{i=1}^k x_i}{\displaystyle\sum_{i=1}^k n_i}=\cfrac{x_1+x_2+\dots+x_k}{n_1+n_2+\dots+n_k}$

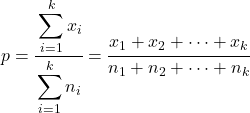
สูตรในการหาสถิติการทดสอบสมมติฐานสำหรับสัดส่วนตัวอย่าง k คือ:

$\displaystyle \chi^2 =\sum_{i=1}^k \frac{(x_i-e_i)^2}{e_i}$

$\displaystyle\chi^2 = \frac{(x_1-e_1)^2}{e_1} +\frac{(x_2-e_2)^2}{e_2} +\dots+\frac{(x_k-e_k)^2}{e_k}$

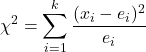
ทอง:

$\chi^2$

คือสถิติการทดสอบสมมติฐานสำหรับสัดส่วนตัวอย่าง k ในกรณีนี้ สถิติเป็นไปตามการแจกแจงแบบไคสแควร์
$x_i$

คือจำนวนผลลัพธ์ในกลุ่มตัวอย่าง i
$n_i$

คือขนาดตัวอย่าง i
$p$

คือสัดส่วนรวมของกลุ่มตัวอย่างทั้งหมด
$e_i$

คือจำนวน Hit ที่คาดหวังจากตัวอย่าง i คำนวณโดยการคูณสัดส่วนรวม

$p$

ตามขนาดตัวอย่าง

$n_i$

.

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม

การทดสอบสมมติฐานเพื่อสัดส่วนคืออะไร?

สูตรทดสอบสมมุติฐานสำหรับสัดส่วน

ตัวอย่างการทดสอบสมมติฐานสำหรับสัดส่วน

การทดสอบสมมติฐานสำหรับสัดส่วนตัวอย่างสองสัดส่วน

การทดสอบสมมติฐานสำหรับสัดส่วนตัวอย่าง k

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

เพิ่มความคิดเห็น