การทดสอบสมมติฐานเพื่อหาความแปรปรวน

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 3, 2023 สถิติ 0 ความคิดเห็น

บทความนี้จะอธิบายว่าการทดสอบสมมติฐานสำหรับความแปรปรวนคืออะไร ดังนั้น คุณจะพบสูตรสำหรับการทดสอบสมมติฐานความแปรปรวน และยังมีแบบฝึกหัดที่แก้ไขทีละขั้นตอนอีกด้วย

การทดสอบสมมติฐานสำหรับความแปรปรวนคืออะไร?

การทดสอบสมมติฐานสำหรับความแปรปรวน เป็นวิธีการทางสถิติที่ใช้ในการพิจารณาว่าจะปฏิเสธสมมติฐานว่างของความแปรปรวนของประชากรหรือไม่ กล่าวอีกนัยหนึ่ง การทดสอบสมมติฐานความแปรปรวนใช้เพื่อปฏิเสธหรือยอมรับสมมติฐานเกี่ยวกับมูลค่าของความแปรปรวนของประชากร

โดยเฉพาะอย่างยิ่ง ขึ้นอยู่กับค่าของสถิติการทดสอบสมมติฐานสำหรับความแปรปรวนและระดับนัยสำคัญที่เลือก สมมติฐานว่างจะถูกปฏิเสธหรือยอมรับ

โปรดทราบว่าการทดสอบสมมติฐานมีชื่อเรียกหลายชื่อ และอาจเรียกว่าการเปรียบเทียบความแตกต่างของสมมติฐาน การทดสอบสมมติฐาน หรือการทดสอบนัยสำคัญ

สูตรการทดสอบสมมติฐานสำหรับความแปรปรวน

สถิติการทดสอบสมมติฐานสำหรับความแปรปรวนจะเท่ากับความแตกต่างระหว่างขนาดตัวอย่างลบหนึ่งเท่าของความแปรปรวนตัวอย่าง และหารด้วยค่าที่เสนอของความแปรปรวนประชากร สถิติการทดสอบสมมติฐานสำหรับความแปรปรวนมี การแจกแจงแบบไคสแควร์

ดังนั้น สูตรในการคำนวณสถิติการทดสอบสมมติฐานสำหรับความแปรปรวน จึงเป็นดังนี้

$\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

ทอง:

$\chi^2$

คือสถิติการทดสอบสมมติฐานสำหรับความแปรปรวน ซึ่งมีการแจกแจงแบบไคสแควร์
$n$

คือขนาดตัวอย่าง
$s^2$

คือความแปรปรวนตัวอย่าง
$\sigma^2$

คือความแปรปรวนของประชากรที่เสนอ

ในการตีความผลลัพธ์ของสถิติ ค่าที่ได้รับจะต้องเปรียบเทียบกับค่าวิกฤตของการทดสอบ

หากการทดสอบสมมติฐานสำหรับความแปรปรวนเป็นแบบสองด้าน สมมติฐานว่างจะถูกปฏิเสธหากสถิติมีค่ามากกว่าค่าวิกฤต
$\chi_{1-\alpha/2|n-1}^2$

หรือถ้าค่าวิกฤตน้อยกว่า

$\chi_{\alpha/2|n-1}$

.
หากการทดสอบสมมติฐานสำหรับความแปรปรวนตรงกับส่วนท้ายด้านขวา สมมติฐานว่างจะถูกปฏิเสธหากสถิติมากกว่าค่าวิกฤต
$\chi_{1-\alpha|n-1}^2$

.
หากการทดสอบสมมติฐานสำหรับความแปรปรวนตรงกับหางซ้าย สมมติฐานว่างจะถูกปฏิเสธหากสถิติน้อยกว่าค่าวิกฤต
$\chi_{\alpha|n-1}$

.

$\begin{array}{l}H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha/2|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si }\chi^2<\chi^2_{\alpha/2|n-1}\text{ se rechaza } H_0 \\[3ex]H_1: \sigma^2> \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2< \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2<\chi^2_{\alpha|n-1}\text{ se rechaza } H_0\end{array}$

ค่าทดสอบสมมติฐานที่สำคัญสำหรับความแปรปรวนได้มาจากตารางการแจกแจงไคสแควร์ โปรดทราบว่าระดับความอิสระของการแจกแจงแบบไคสแควร์คือขนาดตัวอย่างลบ 1

ตัวอย่างการทดสอบสมมุติฐานสำหรับความแปรปรวนในโลกแห่งความเป็นจริง

หลังจากดูคำจำกัดความของการทดสอบสมมติฐานความแปรปรวนและสูตรของมันแล้ว เราจะเห็นตัวอย่างที่เป็นรูปธรรมเพื่อดูดซับแนวคิดนี้ให้เสร็จสิ้น

โรงงานแห่งหนึ่งมีเครื่องจักรที่ผลิตชิ้นส่วนสำหรับรถยนต์ที่มีความแม่นยำสูง อย่างไรก็ตาม เป็นที่สงสัยว่าได้ย้ายออกไปแล้วและตอนนี้ผลิตชิ้นส่วนที่มีช่องว่างมากกว่า 8 มม. ² เพื่อหักล้างสมมติฐานนี้ จะมีการวิเคราะห์ตัวอย่าง 25 ชิ้น และความแปรปรวนของตัวอย่างคือ 9.1 มม. ² สมมติฐานเริ่มแรกสามารถปฏิเสธด้วยระดับนัยสำคัญ α=0.05 ได้หรือไม่

สมมติฐานว่างและสมมติฐานทางเลือกสำหรับการทดสอบสมมติฐานความแปรปรวนมีดังต่อไปนี้:

$\begin{cases}H_0: \sigma^2=8 \\[2ex] H_1:\sigma^2>8 \end{cases}” title=”Rendered by QuickLaTeX.com” height=”65″ width=”101″ style=”vertical-align: 0px;”> ในการพิจารณาว่าสามารถปฏิเสธสมมติฐานว่างได้หรือไม่ เราจะคำนวณสถิติการทดสอบสมมติฐานสำหรับความแปรปรวนโดยใช้สูตรที่เราเห็นด้านบน: <p class=$ $\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

$\chi^2=\cfrac{(25-1)\cdot 9,1}{8}$

$\chi^2=27,3$

ตอนนี้เรามองหาค่าวิกฤตที่สอดคล้องกับส่วนหางด้านขวาของความอิสระ 24 องศา และระดับนัยสำคัญ α=0.05 ในตารางการแจกแจงไคสแควร์:

$\begin{array}{c}\chi^2_{1-\alpha|n-1}=\ \color{orange}\bm{?}\color{black}\\[2ex]\chi^2_{0,95|24}=36,415\end{array}$

ดังนั้น สถิติที่คำนวณได้จึงน้อยกว่าค่าวิกฤตของการทดสอบ ดังนั้นสมมติฐานว่างของการทดสอบสมมติฐานความแปรปรวนจึงไม่ถูกปฏิเสธ แต่สมมติฐานทางเลือกกลับถูกปฏิเสธ

$27,3<36,415 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{No se rechaza } H_0$

➤ ดู: การทดสอบสมมุติฐานสำหรับค่าเฉลี่ยประชากร
➤ ดู: การทดสอบสมมุติฐานสำหรับสัดส่วนประชากร

การทดสอบสมมติฐานสำหรับความแปรปรวนของประชากรสองกลุ่ม

การทดสอบสมมติฐานความแปรปรวนของประชากรสองกลุ่ม ใช้เพื่อปฏิเสธหรือยอมรับสมมติฐานที่ว่าความแปรปรวนของประชากรสองกลุ่มมีค่าเท่ากัน

ดังนั้น สมมติฐานว่างของการทดสอบสมมติฐานเกี่ยวกับความแปรปรวนของประชากรทั้งสองจะเป็นดังนี้เสมอ:

$H_0: \sigma^2_1=\sigma^2_2$

และสมมติฐานทางเลือกอาจเป็นหนึ่งในสามตัวเลือก:

$\begin{array}{l}H_1:\sigma^2_1\neq \sigma^2_2\\[2ex]H_1:\sigma^2_1>\sigma^2_2\\[2ex]H_1:\sigma^2_1<\sigma^2_2\end{array}$

ในกรณีนี้ สูตรคำนวณสถิติการทดสอบสมมติฐานสำหรับความแปรปรวนของประชากรทั้งสองคือ

$F=\cfrac{s_1^2}{s_2^2}$

ทอง:

$F$

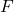
คือสถิติการทดสอบสมมติฐานสำหรับความแปรปรวนของประชากรสองกลุ่ม ซึ่งเป็นไปตาม การแจกแจงแบบ F
$\sigma_1^2$

คือความแปรปรวนของประชากร 1
$\sigma_2^2$

คือความแปรปรวนของประชากร 2
$s_1^2$

คือความแปรปรวนของกลุ่มตัวอย่างที่ 1
$s_2^2$

คือความแปรปรวนของกลุ่มตัวอย่าง 2
$n_1$

คือขนาดตัวอย่างที่ 1
$n_2$

คือขนาดตัวอย่างที่ 2

เนื่องจากการแจกแจง Snedecor F ไม่สมมาตร สมมติฐานว่างจึงถูกปฏิเสธตามเกณฑ์ต่อไปนี้:

[latex]\begin{array}{l}H_1: \sigma_1^2\neq \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } F>F_{ 1-\alpha/2|n_1-1|n_2-1}\text{ ติดตามอีกครั้ง } H_0\\[3ex]H_1: \sigma_1^2\neq \sigma_2^2 \ \color{orange}\bm{\longrightarrow }\color{black} \ \text{ถ้า }F \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{If } F>F_{1-\alpha|n_1-1|n_2-1}\text{ ติดตาม } H_0\\[3ex]H_1: \sigma_1^2< \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } F

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม