วิธีทำการทดสอบอันดับแบบลงนามของ wilcoxon
การทดสอบอันดับแบบลงชื่อของ Wilcoxon เป็นเวอร์ชันที่ไม่มีพารามิเตอร์ของ การทดสอบแบบจับคู่ ใช้เพื่อทดสอบว่ามีความแตกต่างที่มีนัยสำคัญระหว่างค่าเฉลี่ยประชากรสองค่าหรือไม่
เมื่อใดจึงควรใช้การทดสอบอันดับแบบลงนามของ Wilcoxon
ใช้การทดสอบ Wilcoxon Signed Rank เมื่อคุณต้องการใช้การทดสอบ paired t แต่การกระจายตัวของความแตกต่างระหว่างคู่นั้นมี การกระจายแบบไม่ปกติ อย่างรุนแรง
วิธีที่ง่ายที่สุดในการพิจารณาว่าความแตกต่างนั้นไม่มีการกระจายแบบปกติหรือไม่ คือการสร้างฮิสโตแกรมของความแตกต่าง และดูว่าพวกมันเป็นไปตามการกระจายแบบ “ระฆัง” ที่ค่อนข้างปกติหรือไม่
โปรดจำไว้ว่าการทดสอบ paired t นั้นค่อนข้างทนทานต่อการเบี่ยงเบนไปจากภาวะปกติ ดังนั้นค่าเบี่ยงเบนจากการแจกแจงแบบปกติจะต้องมีขนาดใหญ่พอที่จะพิสูจน์ให้เห็นถึงการใช้การทดสอบ Wilcoxon Signed Rank
วิธีทำการทดสอบอันดับแบบลงนามของ Wilcoxon
ตัวอย่างต่อไปนี้แสดงวิธีดำเนินการทดสอบ Wilcoxon Signed Rank
โค้ชบาสเก็ตบอลต้องการทราบว่าโปรแกรมการฝึกซ้อมบางอย่างจะเพิ่มจำนวนการโยนโทษของผู้เล่นของเขาหรือไม่ เพื่อทดสอบสิ่งนี้ เขาขอให้ผู้เล่น 15 คนโยนโทษ 20 ครั้งก่อนและหลังโปรแกรมการฝึกซ้อม
เนื่องจากผู้เล่นแต่ละคนสามารถ “จับคู่” กับตัวเองได้ โค้ชจึงวางแผนที่จะใช้การทดสอบแบบจับคู่เพื่อพิจารณาว่ามีความแตกต่างอย่างมีนัยสำคัญระหว่างจำนวนการโยนโทษโดยเฉลี่ยก่อนและหลังโปรแกรมการฝึกซ้อมหรือไม่ การฝึกอบรม.
อย่างไรก็ตาม การกระจายความแตกต่างกลายเป็นเรื่องไม่ปกติ ซึ่งเป็นสาเหตุที่โค้ชใช้การทดสอบอันดับแบบลงนามของ Wilcoxon แทน
ตารางต่อไปนี้แสดงจำนวนการโยนโทษ (จากความพยายาม 20 ครั้ง) โดยผู้เล่นแต่ละคนจาก 15 คน ก่อนและหลังโปรแกรมการฝึกซ้อม:
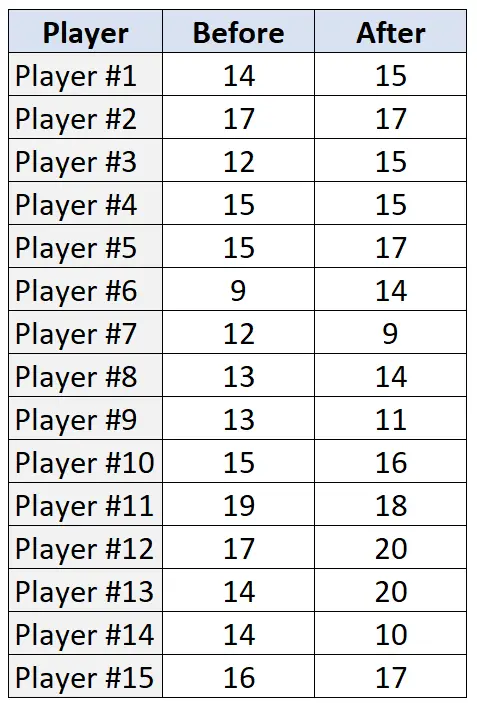
ขั้นตอนที่ 1: ระบุสมมติฐานว่างและทางเลือก
H 0 : ค่ามัธยฐานความแตกต่างระหว่างทั้งสองกลุ่มคือศูนย์
HA : ส่วนต่างค่ามัธยฐานเป็นลบ (เช่น ผู้เล่นโยนโทษน้อยลงก่อนเข้าร่วมโปรแกรมการฝึกซ้อม)
ขั้นตอนที่ 2: ค้นหาความแตกต่างและความแตกต่างสัมบูรณ์สำหรับแต่ละคู่
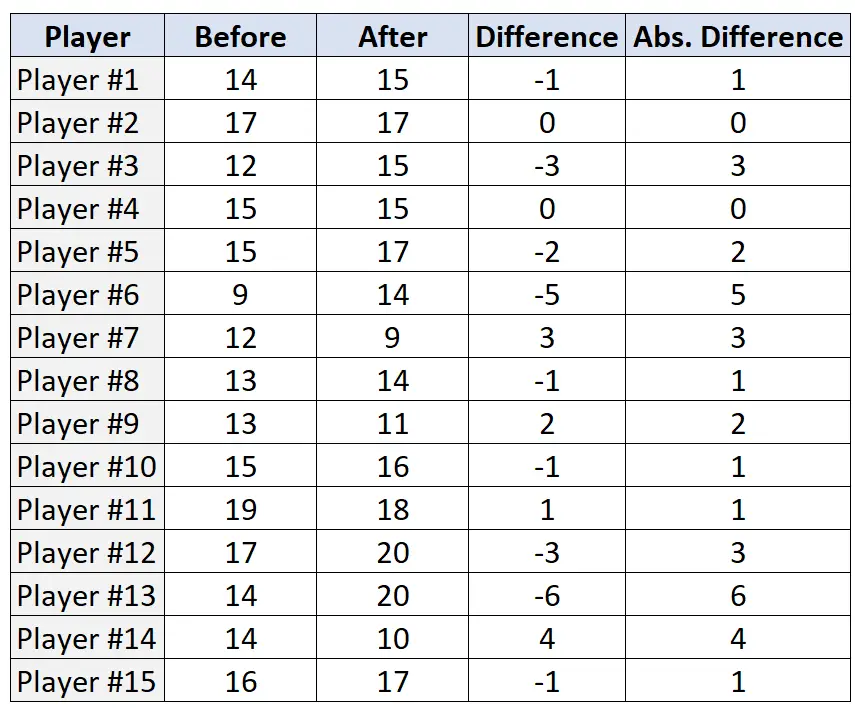
ขั้นตอนที่ 3: จัดอันดับคู่เงินตามผลต่างสัมบูรณ์และกำหนดอันดับจากผลต่างสัมบูรณ์ที่น้อยที่สุดไปใหญ่ที่สุด ไม่สนใจคู่ที่มีผลต่างสัมบูรณ์เป็น “0” และกำหนดอันดับเฉลี่ยในกรณีที่เสมอกัน
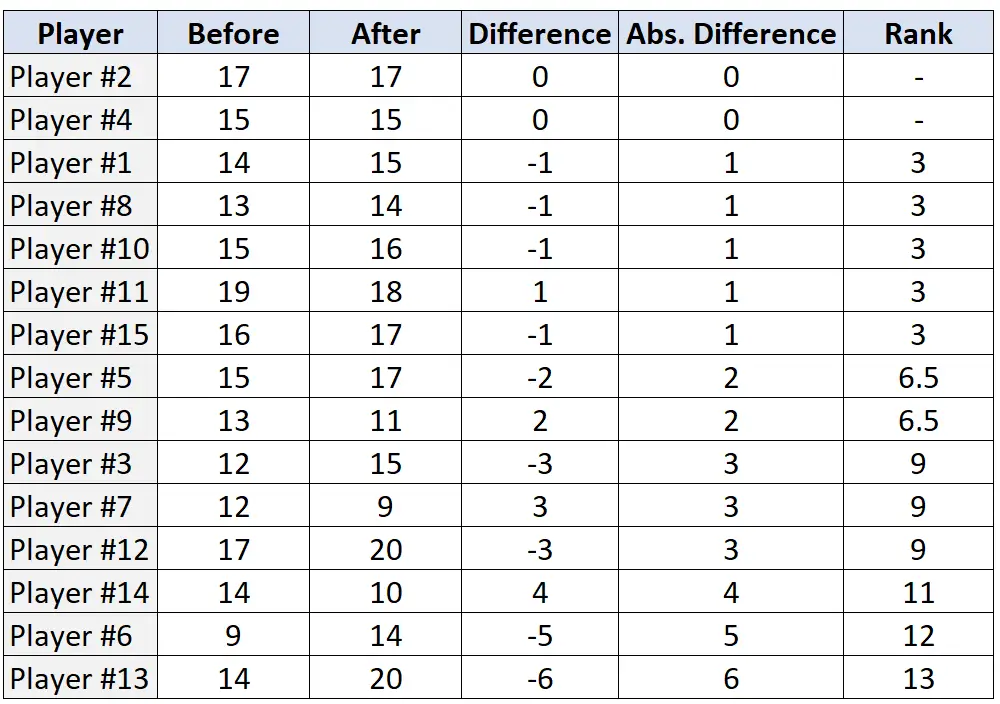
ขั้นตอนที่ 4: ค้นหาผลรวมของอันดับบวกและอันดับลบ
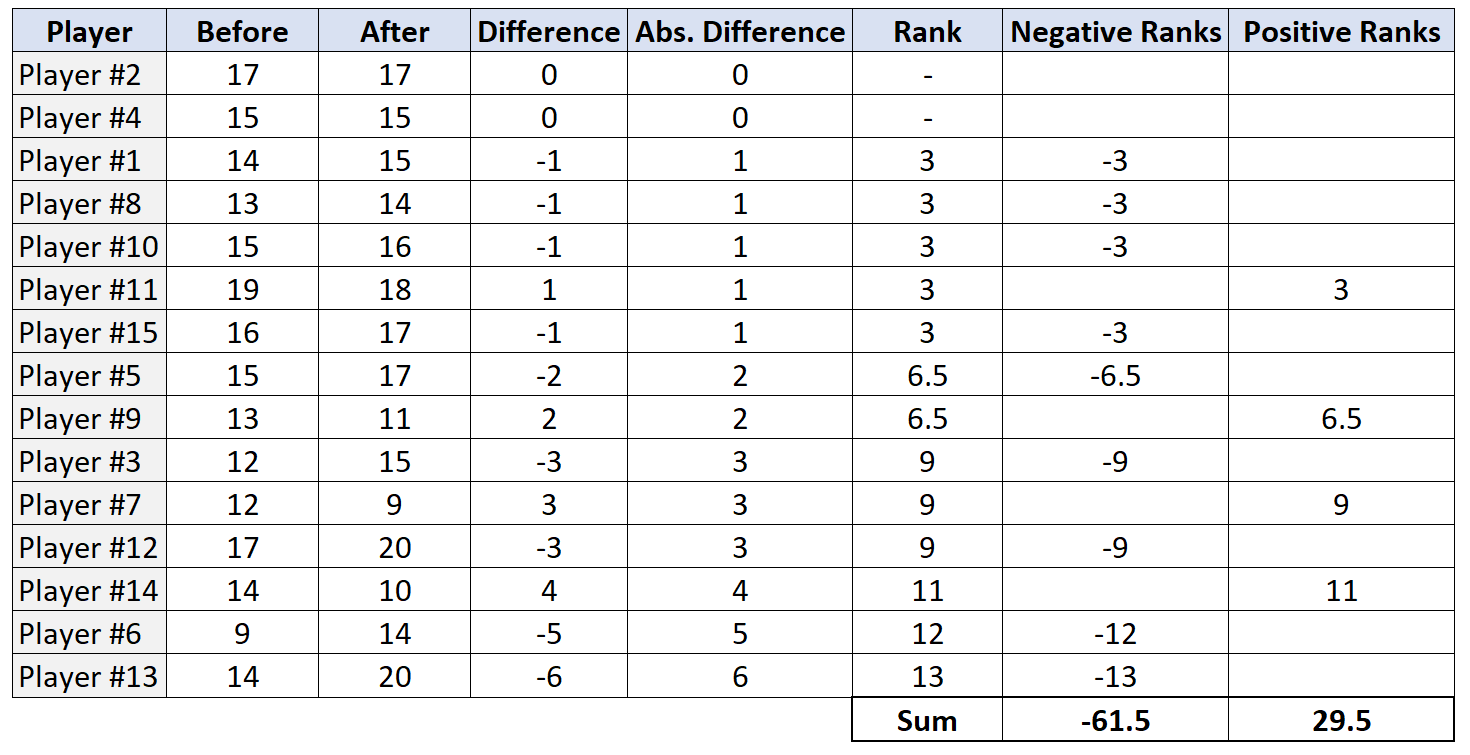
ขั้นตอนที่ 5: ปฏิเสธหรือไม่ปฏิเสธสมมติฐานว่าง
สถิติการทดสอบ W คือค่าที่น้อยที่สุดของค่าสัมบูรณ์ของอันดับบวกและอันดับลบ ในกรณีนี้ ค่าที่น้อยที่สุดคือ 29.5 ดังนั้นสถิติการทดสอบของเราคือ W = 29.5
เพื่อพิจารณาว่าเราควรปฏิเสธสมมติฐานว่างหรือไม่ เราสามารถอ้างอิงถึงค่าวิกฤตที่พบใน ตารางค่าวิกฤตการทดสอบอันดับของ Wilcoxon ซึ่งสอดคล้องกับ n และระดับอัลฟ่าที่เลือก
หากสถิติการทดสอบของเรา W น้อยกว่าหรือเท่ากับ ค่าวิกฤตในตาราง เราสามารถปฏิเสธสมมติฐานว่างได้ มิฉะนั้น เราจะล้มเหลวในการปฏิเสธสมมติฐานที่เป็นโมฆะ
ค่าวิกฤตที่สอดคล้องกับระดับอัลฟา 0.05 และ n = 13 (จำนวนคู่ทั้งหมดลบสองคู่ที่เราไม่ได้คำนวณอันดับเนื่องจากมีความแตกต่างที่สังเกตได้เป็น 0) คือ 17
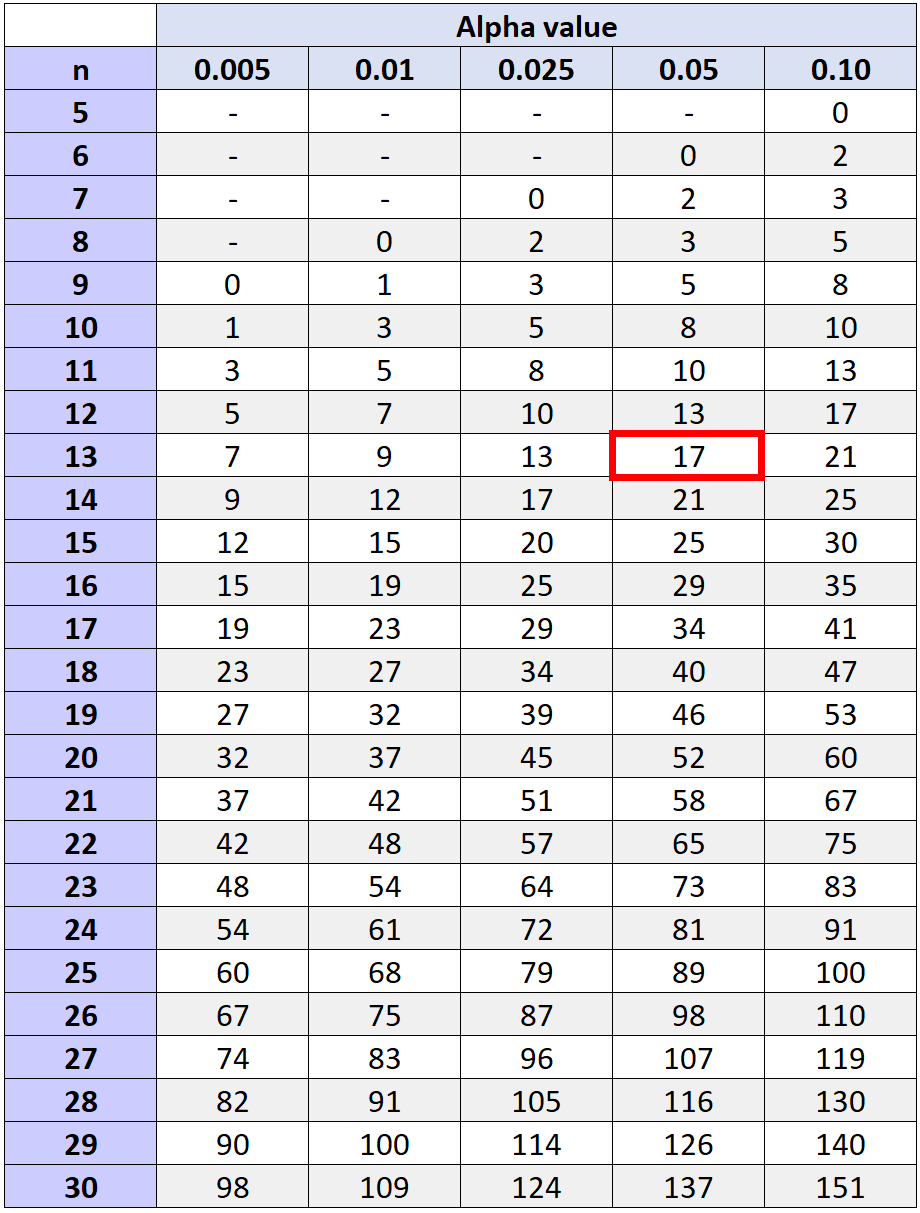
เนื่องจากสถิติการทดสอบของเรา (W = 29.5) ไม่น้อยกว่าหรือเท่ากับ 17 เราจึงไม่สามารถปฏิเสธสมมติฐานว่างได้ เราไม่มีหลักฐานเพียงพอที่จะกล่าวว่าโปรแกรมการฝึกซ้อมส่งผลให้จำนวนการโยนโทษของผู้เล่นเพิ่มขึ้นอย่างมาก
หมายเหตุ: ใช้ เครื่องคำนวณการทดสอบอันดับที่มีลายเซ็นของ Wilcoxon หากคุณต้องการทำการทดสอบโดยใช้เครื่องคิดเลขแทนที่จะใช้ด้วยมือ