วิธีดำเนินการทดสอบ mcnemar ใน spss
การทดสอบ McNemar ใช้เพื่อพิจารณาว่าสัดส่วนระหว่างข้อมูลที่จับคู่มีความแตกต่างกันอย่างมีนัยสำคัญทางสถิติหรือไม่
บทช่วยสอนนี้จะอธิบายวิธีดำเนินการทดสอบ McNemar ใน SPSS
ตัวอย่าง: การทดสอบ McNemar ใน SPSS
สมมติว่านักวิจัยต้องการทราบว่าวิดีโอการตลาดบางรายการสามารถเปลี่ยนความคิดเห็นของผู้คนเกี่ยวกับกฎหมายข้อใดข้อหนึ่งได้หรือไม่ พวกเขาสัมภาษณ์คน 25 คนเพื่อดูว่าพวกเขาสนับสนุนกฎหมายหรือไม่ จากนั้นพวกเขาก็ฉายวิดีโอการตลาดให้ทั้ง 25 คนฟัง และสัมภาษณ์พวกเขาอีกครั้งหลังจากวิดีโอจบ
ตารางต่อไปนี้แสดงจำนวนผู้ที่สนับสนุนกฎหมายก่อนและหลังดูวิดีโอ:
| วีดีโอก่อนทำการตลาด | ||
|---|---|---|
| วิดีโอหลังการตลาด | ไม่สนับสนุน | สนับสนุน |
| ไม่สนับสนุน | 7 | 5 |
| สนับสนุน | 3 | สิบ |
เพื่อตรวจสอบว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติในสัดส่วนของผู้ที่สนับสนุนกฎหมายก่อนและหลังดูวิดีโอหรือไม่ เราสามารถใช้ขั้นตอนต่อไปนี้เพื่อทำการทดสอบ McNemar ใน SPSS:
ขั้นตอนที่ 1: ป้อนข้อมูล
ขั้นแรกให้ป้อนข้อมูลตามที่แสดงด้านล่าง:
แต่ละแถวจะแสดง ID ของแต่ละบุคคล ตำแหน่งก่อนดูวิดีโอการตลาด และตำแหน่งหลังจากดูวิดีโอการตลาด
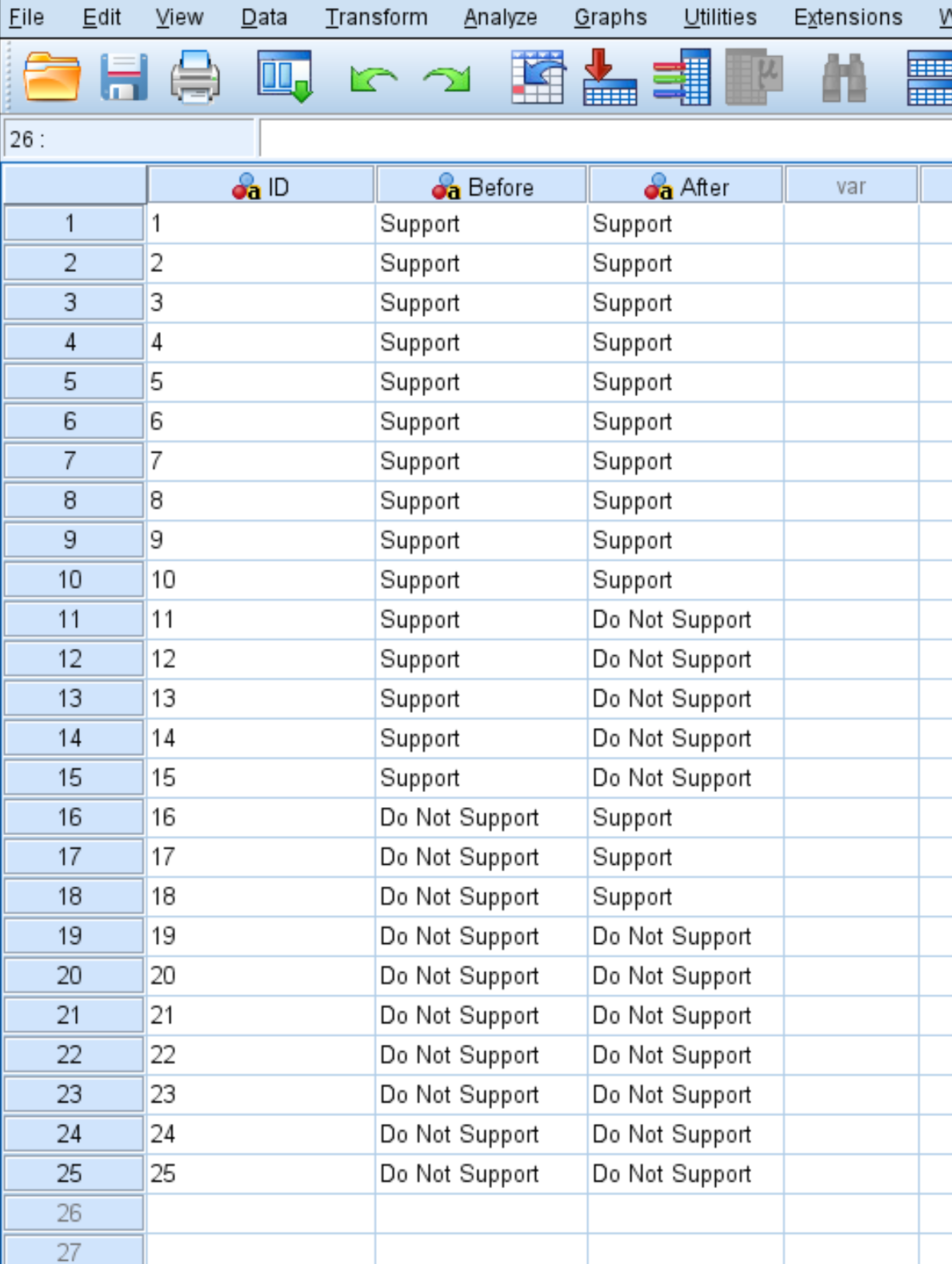
ขั้นตอนที่ 2: ทำการทดสอบ McNemar
คลิกแท็บ วิเคราะห์ จากนั้นคลิก สถิติเชิงพรรณนา จากนั้นคลิก ครอสแท็บ :
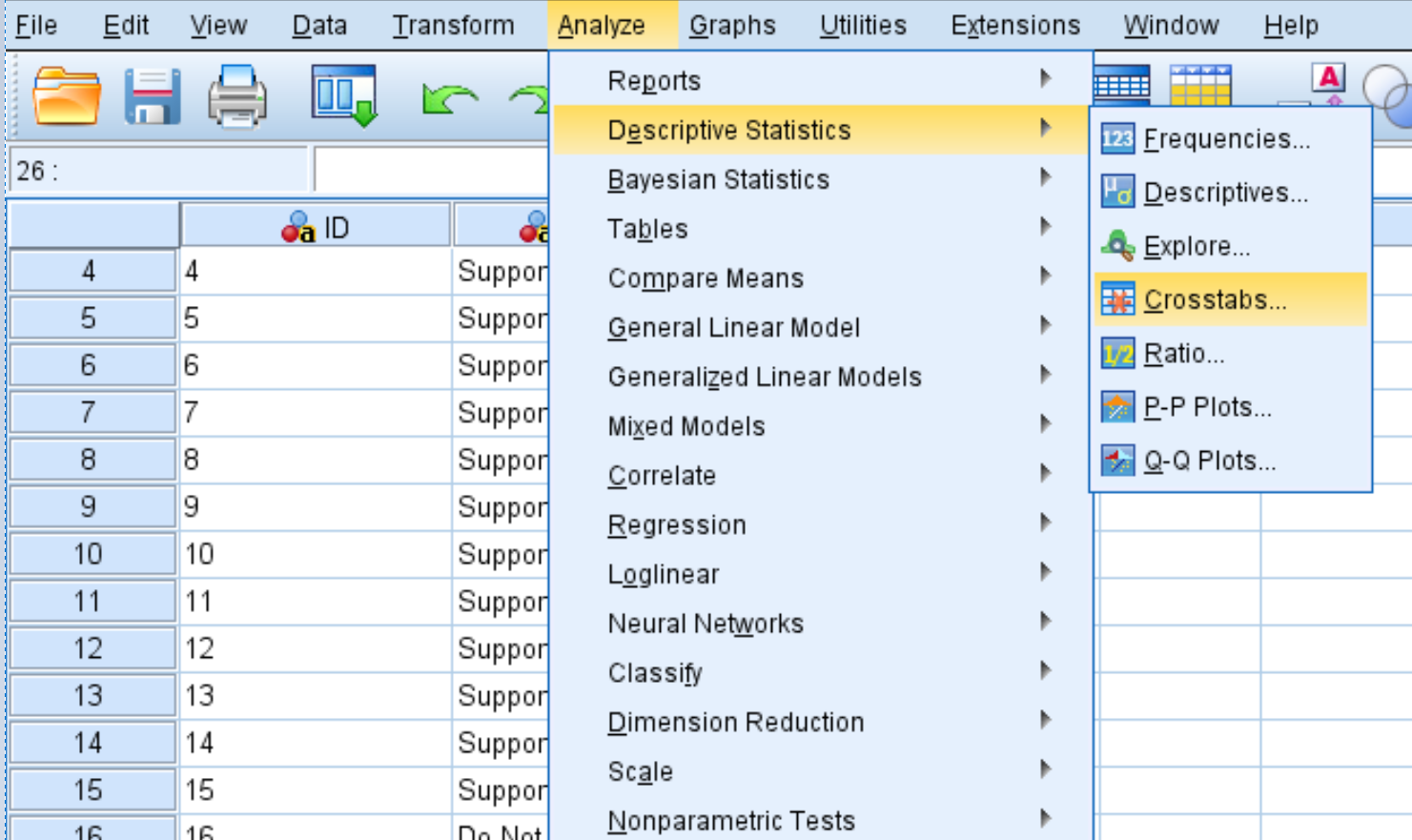
ลากตัวแปร After ลงในพื้นที่ชื่อ Rows และตัวแปร Before ลงในพื้นที่ชื่อ Columns จากนั้นคลิกปุ่มที่มีข้อความว่า สถิติ และตรวจดูให้แน่ใจว่าได้ทำเครื่องหมายในช่องถัดจาก McNemar แล้ว จากนั้นคลิก ดำเนินการต่อ จากนั้นคลิก ตกลง
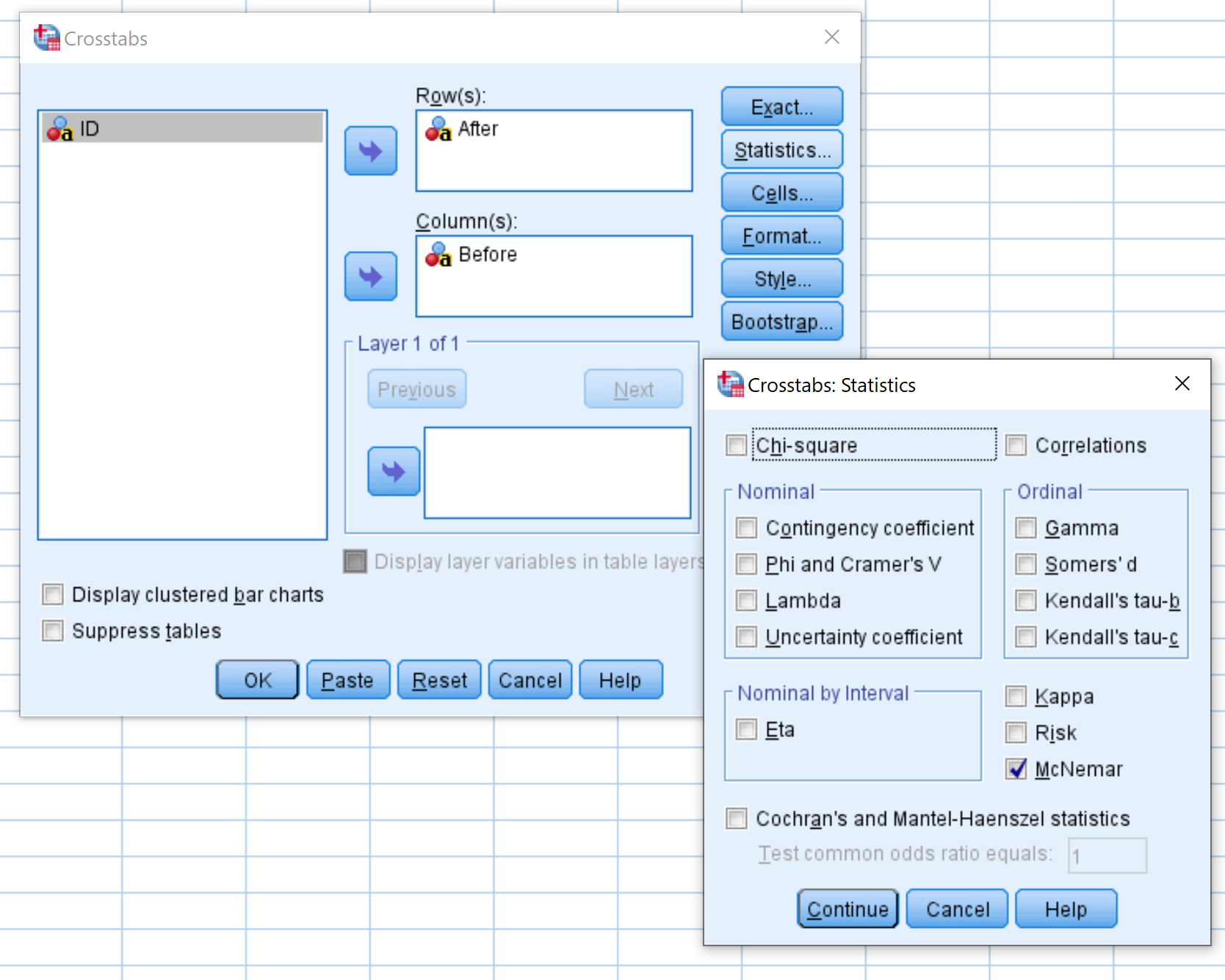
ขั้นตอนที่ 3: ตีความผลลัพธ์
เมื่อคุณคลิก ตกลง ผลการทดสอบของ McNemar จะปรากฏขึ้น:
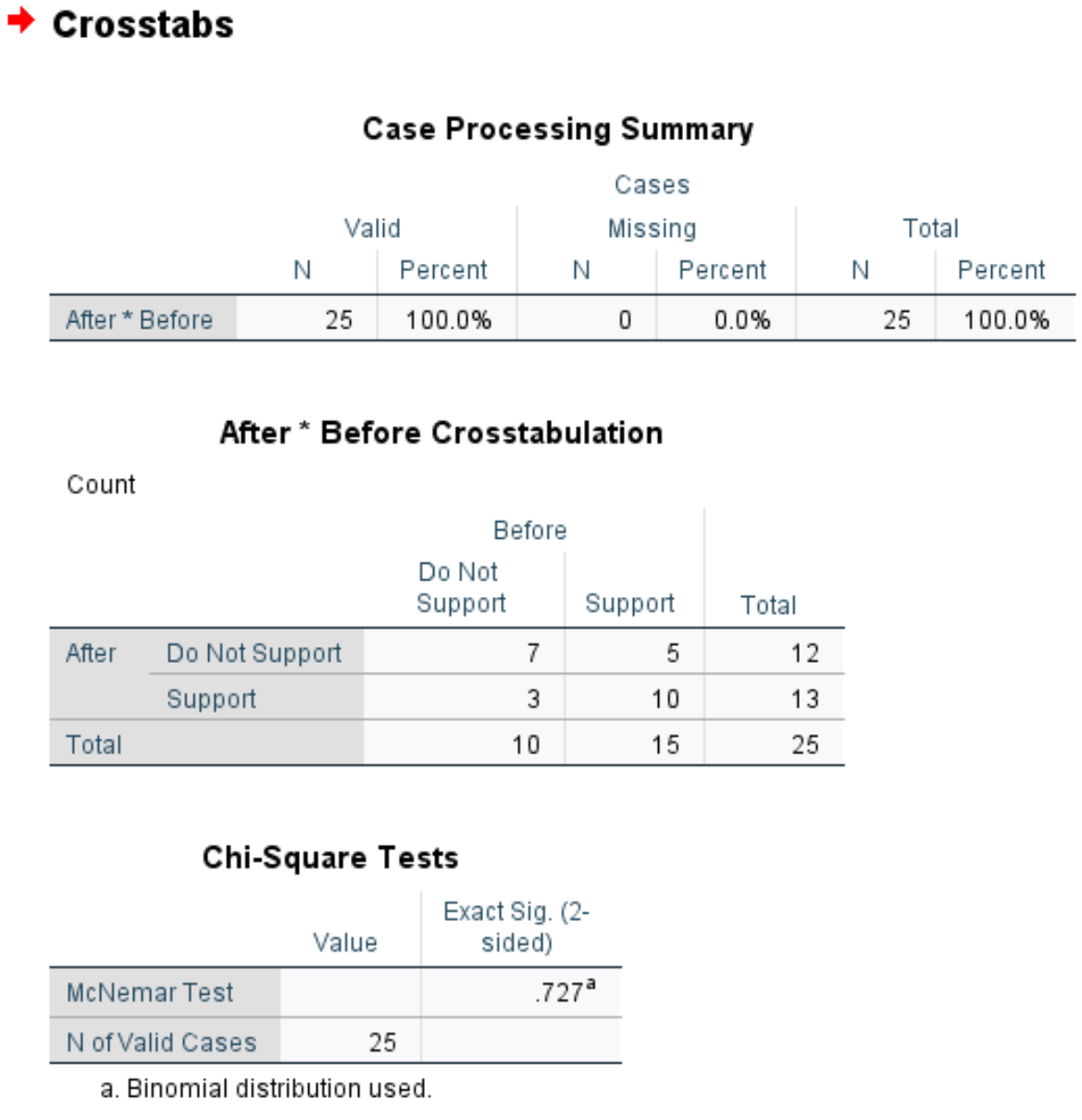
ตารางแรกแสดงจำนวนกรณีที่หายไปในชุดข้อมูล เราจะเห็นว่ามี 0 กรณีหายไปในตัวอย่างนี้
ตารางที่สองแสดงตารางไขว้ของจำนวนบุคคลที่สนับสนุนหรือไม่สนับสนุนกฎหมายก่อนและหลังดูวิดีโอการตลาด
ตารางที่สามแสดงผลการทดสอบ McNemar ค่า p ของการทดสอบคือ 0.727 เนื่องจากค่านี้ไม่น้อยกว่า 0.05 เราจึงไม่มีหลักฐานเพียงพอที่จะกล่าวว่าสัดส่วนของผู้ที่สนับสนุนกฎหมายก่อนและหลังดูวิดีโอการตลาดมีความแตกต่างกันอย่างมีนัยสำคัญทางสถิติ
หมายเหตุเกี่ยวกับการคำนวณค่า p
รับตาราง 2×2 ต่อไปนี้:
| วีดีโอก่อนทำการตลาด | ||
|---|---|---|
| วิดีโอหลังการตลาด | ไม่สนับสนุน | สนับสนุน |
| ไม่สนับสนุน | มี | บี |
| สนับสนุน | VS | ดี |
SPSS ใช้สูตร (|BC| – 1) 2 / (B+C) เพื่อคำนวณสถิติการทดสอบไคสแควร์
ในตัวอย่างนี้ สถิติการทดสอบไคสแควร์คือ (|5-3| – 1) 2 / (5+3) = 1/8 = 0.125
ค่า p สอดคล้องกับสถิติการทดสอบไคสแควร์ที่มีอิสระ 1 องศา เมื่อใช้ เครื่องคำนวณไคสแควร์ถึงค่า P เราพบว่าค่าไคสแควร์ 0.125 โดยมีอิสระ 1 องศา เท่ากับค่า p 0.727