วิธีทำการทดสอบ tukey ใน r
การวิเคราะห์ความแปรปรวนแบบทางเดียว ใช้เพื่อพิจารณาว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างค่าเฉลี่ยของกลุ่มอิสระสามกลุ่มขึ้นไปหรือไม่
หาก ค่า p-value โดยรวมของตาราง ANOVA ต่ำกว่าระดับนัยสำคัญที่กำหนด เราก็มีหลักฐานเพียงพอที่จะบอกว่าค่าเฉลี่ยของกลุ่มอย่างน้อยหนึ่งรายการแตกต่างจากค่าเฉลี่ยอื่นๆ
อย่างไรก็ตาม นี่ไม่ได้บอกเราว่ากลุ่ม ใด มีความแตกต่างกัน นี่บอกเราว่าค่าเฉลี่ยกลุ่มไม่เท่ากันทั้งหมด หากต้องการทราบว่ากลุ่มใดมีความแตกต่างกัน เราจำเป็นต้องทำการ ทดสอบหลังการทดสอบ
การทดสอบหลังการทดสอบที่ใช้กันมากที่สุดอย่างหนึ่งคือ การทดสอบ Tukey ซึ่งช่วยให้เราทำการเปรียบเทียบแบบคู่ระหว่างค่าเฉลี่ยของแต่ละกลุ่มในขณะที่ควบคุม อัตราความผิดพลาดแบบครอบครัว
บทช่วยสอนนี้จะอธิบายวิธีดำเนินการทดสอบ Tukey ใน R
หมายเหตุ: หากกลุ่มใดในการศึกษาของคุณถือเป็นกลุ่มควบคุม คุณควรใช้ การทดสอบของ Dunnett เป็นแบบทดสอบหลังการทดสอบแทน
ตัวอย่าง: การทดสอบ Tukey ใน R
ขั้นตอนที่ 1: ติดตั้งโมเดล ANOVA
รหัสต่อไปนี้แสดงวิธีสร้างชุดข้อมูลปลอมที่มีสามกลุ่ม (A, B และ C) และปรับแบบจำลองการวิเคราะห์ความแปรปรวนแบบทางเดียวให้กับข้อมูลเพื่อพิจารณาว่าค่าเฉลี่ยของแต่ละกลุ่มเท่ากันหรือไม่:
#make this example reproducible set.seed(0) #create data data <- data.frame(group = rep (c("A", "B", "C"), each = 30), values = c(runif(30, 0, 3), runif(30, 0, 5), runif(30, 1, 7))) #view first six rows of data head(data) group values 1 A 2.6900916 2 A 0.7965260 3 A 1.1163717 4 A 1.7185601 5 A 2.7246234 6 A 0.6050458 #fit one-way ANOVA model model <- aov (values~group, data=data) #view the model output summary(model) Df Sum Sq Mean Sq F value Pr(>F) group 2 98.93 49.46 30.83 7.55e-11 *** Residuals 87 139.57 1.60 --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
เราจะเห็นว่าค่า p โดยรวมจากตาราง ANOVA คือ 7.55e-11 เนื่องจากตัวเลขนี้น้อยกว่า 0.05 เราจึงมีหลักฐานเพียงพอที่จะบอกว่าค่าเฉลี่ยในแต่ละกลุ่มไม่เท่ากัน ดังนั้นเราจึงสามารถทำการทดสอบ Tukey เพื่อระบุได้อย่างชัดเจนว่าค่าเฉลี่ยของกลุ่มใดที่แตกต่างกัน
ขั้นตอนที่ 2: ทำการทดสอบ Tukey
รหัสต่อไปนี้แสดงวิธีการใช้ฟังก์ชัน TukeyHSD() เพื่อทำการทดสอบ Tukey:
#perform Tukey's Test TukeyHSD(model, conf.level= .95 ) Tukey multiple comparisons of means 95% family-wise confidence level Fit: aov(formula = values ~ group, data = data) $group diff lwr upr p adj BA 0.9777414 0.1979466 1.757536 0.0100545 CA 2.5454024 1.7656076 3.325197 0.0000000 CB 1.5676610 0.7878662 2.347456 0.0000199
ค่า p บ่งชี้ว่าแต่ละโปรแกรมมีความแตกต่างที่มีนัยสำคัญทางสถิติหรือไม่ ผลการวิจัยพบว่าการลดน้ำหนักเฉลี่ยของแต่ละโปรแกรมมีความแตกต่างกันอย่างมีนัยสำคัญทางสถิติที่ระดับนัยสำคัญ 0.05
โดยเฉพาะ:
- ค่า P สำหรับความแตกต่างในค่าเฉลี่ยระหว่าง B และ A: 0.0100545
- ค่า P สำหรับความแตกต่างในค่าเฉลี่ยระหว่าง C และ A: 0.0000000
- ค่า P สำหรับความแตกต่างในค่าเฉลี่ยระหว่าง C และ B: 0.0000199
ขั้นตอนที่ 3: เห็นภาพผลลัพธ์
นอกจากนี้เรายังสามารถใช้ฟังก์ชัน plot(TukeyHSD()) เพื่อแสดงภาพช่วงความเชื่อมั่น:
#plot confidence intervals plot(TukeyHSD(model, conf.level= .95 ), las = 2 )
หมายเหตุ: อาร์กิวเมนต์ las ระบุว่าป้ายกำกับเครื่องหมายต้องตั้งฉาก (las=2) กับแกน
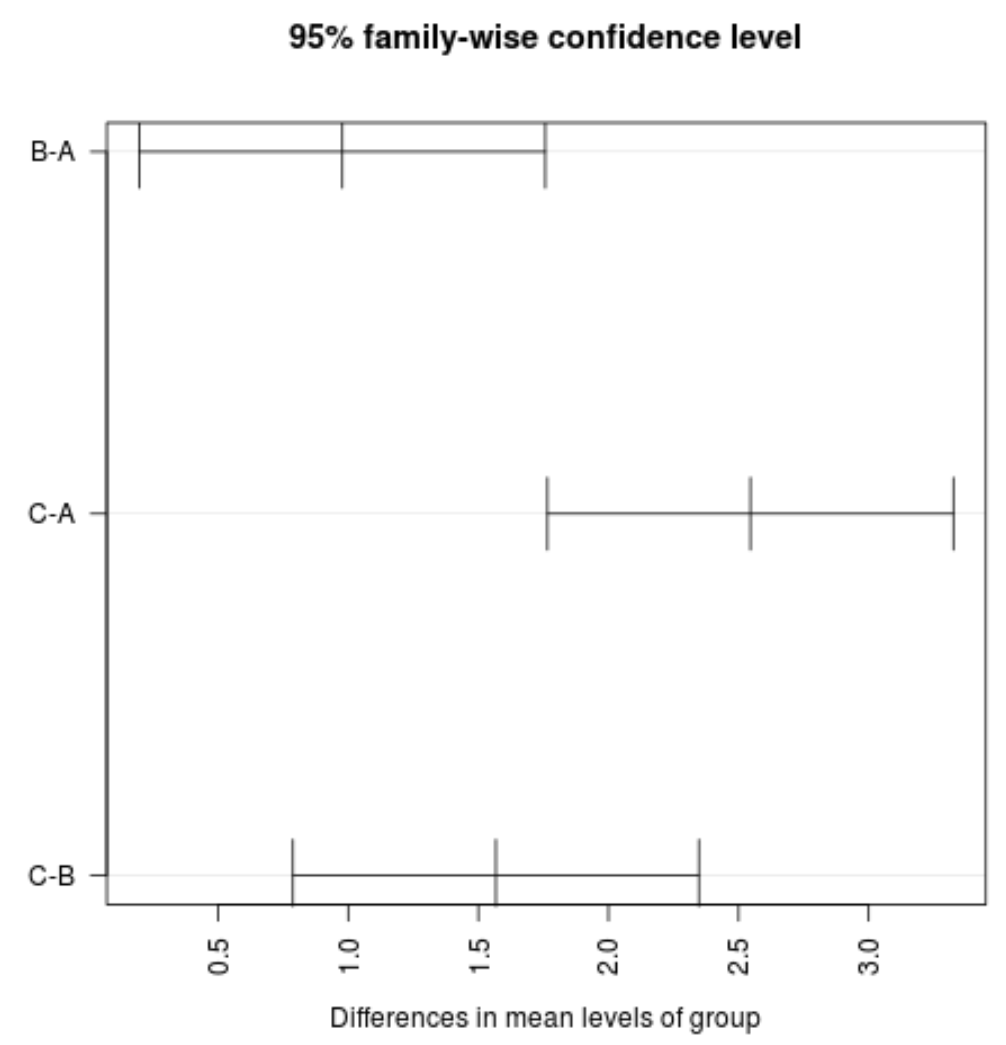
เราจะเห็นว่าช่วงความเชื่อมั่นสำหรับค่าเฉลี่ยระหว่างกลุ่มไม่มีค่าเป็นศูนย์ ซึ่งบ่งชี้ว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติในการสูญเสียเฉลี่ยระหว่างทั้งสามกลุ่ม ซึ่งสอดคล้องกับค่า p ทั้งหมดสำหรับการทดสอบสมมติฐานของเราที่น้อยกว่า 0.05
สำหรับตัวอย่างนี้ เราสามารถสรุปได้ดังต่อไปนี้:
- ค่าเฉลี่ยของกลุ่ม C สูงกว่าค่าเฉลี่ยของกลุ่ม A และ B อย่างมีนัยสำคัญ
- ค่าเฉลี่ยของกลุ่ม B สูงกว่าค่าเฉลี่ยของกลุ่ม A อย่างมีนัยสำคัญ
แหล่งข้อมูลเพิ่มเติม
คู่มือการใช้การทดสอบหลังการทดลองด้วย ANOVA
วิธีดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวใน R
วิธีดำเนินการวิเคราะห์ความแปรปรวนแบบสองทางใน R