อะไรคือข้อแลกเปลี่ยนระหว่างความแปรปรวนและความแปรปรวนในแมชชีนเลิร์นนิง?

ในการประเมินประสิทธิภาพของแบบจำลองในชุดข้อมูล เราจำเป็นต้องวัดว่าการคาดการณ์ของแบบจำลองตรงกับข้อมูลที่สังเกตได้ดีเพียงใด

สำหรับ โมเดลการถดถอย หน่วยเมตริกที่ใช้กันมากที่สุดคือค่าคลาดเคลื่อนกำลังสองเฉลี่ย (MSE) ซึ่งคำนวณได้ดังนี้

MSE = (1/n)*Σ(y _i – f(x _i )) ²

ทอง:

• n: จำนวนการสังเกตทั้งหมด
• y _i : ค่าตอบสนองของการสังเกต ^{ครั้งที่ 3}
• f(x _i ): ค่าตอบสนองที่คาดการณ์ไว้ของการสังเกต ^{ครั้ง} ที่ i

ยิ่งการคาดการณ์แบบจำลองใกล้กับการสังเกตมากเท่าไร MSE ก็จะยิ่งต่ำลงเท่านั้น

อย่างไรก็ตาม เราสนใจเฉพาะ การทดสอบ MSE หรือ MSE เมื่อมีการนำแบบจำลองของเราไปใช้กับข้อมูลที่มองไม่เห็นเท่านั้น เนื่องจากเราสนใจเพียงว่าโมเดลจะทำงานอย่างไรกับข้อมูลที่ไม่รู้จัก ไม่ใช่กับข้อมูลที่มีอยู่

ตัวอย่างเช่น จะไม่เป็นไรหากแบบจำลองที่คาดการณ์ราคาหุ้นมี MSE ต่ำสำหรับข้อมูลในอดีต แต่เรา ต้องการ ที่จะใช้แบบจำลองนี้เพื่อคาดการณ์ข้อมูลในอนาคตได้อย่างแม่นยำ

ปรากฎว่าการทดสอบ MSE ยังคงสามารถแบ่งออกเป็นสองส่วน:

(1) ความแปรปรวน: หมายถึงจำนวนฟังก์ชัน f ของเราที่จะเปลี่ยนแปลงหากเราประมาณค่าโดยใช้ชุดการฝึกอื่น

(2) อคติ: หมายถึงข้อผิดพลาดที่เกิดจากการเข้าถึงปัญหาจริง ซึ่งอาจซับซ้อนมากด้วยแบบจำลองที่ง่ายกว่ามาก

เขียนในแง่คณิตศาสตร์:

การทดสอบ MSE = Var( f̂( x ₀ )) + [อคติ( f̂( x ₀ ))] ² + Var(ε)

การทดสอบ MSE = ความแปรปรวน + อคติ ² + ข้อผิดพลาดที่ลดไม่ได้

คำที่สาม ข้อผิดพลาดที่ลดไม่ได้ คือข้อผิดพลาดที่ไม่สามารถลดได้ด้วยโมเดลใดๆ เพียงเพราะมี สัญญาณรบกวน ในความสัมพันธ์ระหว่างชุดตัวแปรอธิบายและ ตัวแปรตอบสนอง อยู่เสมอ

โมเดลที่มี อคติสูง มักจะมี ความแปรปรวนต่ำ ตัวอย่างเช่น โมเดลการถดถอยเชิงเส้นมีแนวโน้มที่จะมีอคติสูง (สมมติว่ามีความสัมพันธ์เชิงเส้นอย่างง่ายระหว่างตัวแปรอธิบายและตัวแปรตอบสนอง) และความแปรปรวนต่ำ (การประมาณค่าของโมเดลจะไม่เปลี่ยนแปลงมากนักจากตัวอย่างหนึ่งไปยังอีกตัวอย่าง) อื่น ๆ).

อย่างไรก็ตาม โมเดลที่มี อคติต่ำ มักจะมี ความแปรปรวนสูง ตัวอย่างเช่น โมเดลไม่เชิงเส้นที่ซับซ้อนมีแนวโน้มที่จะมีอคติต่ำ (อย่าถือว่ามีความสัมพันธ์บางอย่างระหว่างตัวแปรอธิบายและตัวแปรตอบสนอง) ที่มีความแปรปรวนสูง (การประมาณค่าแบบจำลองสามารถเปลี่ยนแปลงอย่างมีนัยสำคัญจากตัวอย่างการเรียนรู้ไปสู่อีกตัวอย่างหนึ่ง)

การแลกเปลี่ยนความแปรปรวนอคติ

การแลกเปลี่ยนความแปรปรวนอคติ หมายถึงการแลกเปลี่ยนที่เกิดขึ้นเมื่อเราเลือกที่จะลดอคติ ซึ่งโดยทั่วไปจะเพิ่มความแปรปรวน หรือเพื่อลดความแปรปรวน ซึ่งโดยทั่วไปจะเพิ่มอคติ

กราฟต่อไปนี้เสนอวิธีแสดงภาพข้อดีข้อเสียนี้:

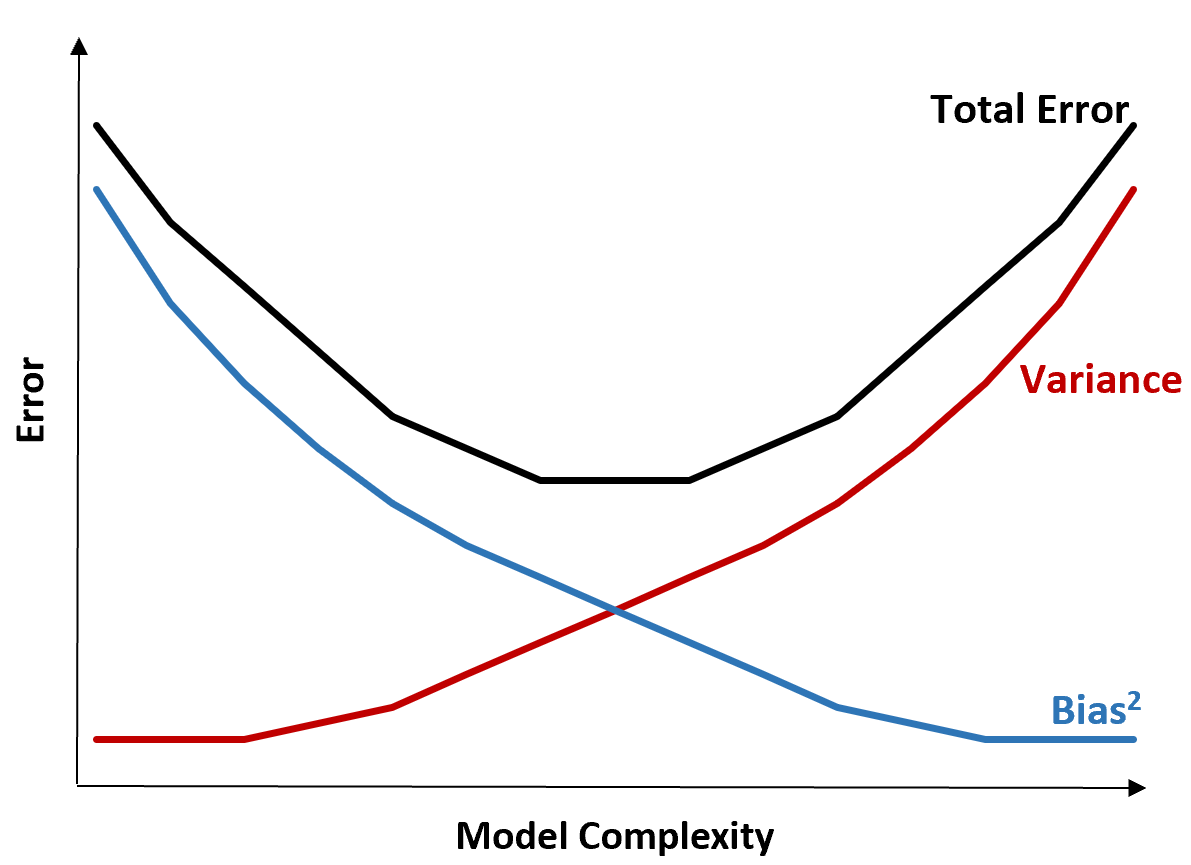
ข้อผิดพลาดทั้งหมดจะลดลงเมื่อความซับซ้อนของแบบจำลองเพิ่มขึ้น แต่จะถึงจุดหนึ่งเท่านั้น เมื่อเลยจุดหนึ่งไปแล้ว ความแปรปรวนเริ่มเพิ่มขึ้น และข้อผิดพลาดทั้งหมดก็เริ่มเพิ่มขึ้นเช่นกัน

ในทางปฏิบัติ เราสนใจแต่เพียงการลดข้อผิดพลาดทั้งหมดของแบบจำลองให้เหลือน้อยที่สุด ไม่จำเป็นต้องลดความแปรปรวนหรืออคติให้เหลือน้อยที่สุด ปรากฎว่าวิธีลดข้อผิดพลาดทั้งหมดให้เหลือน้อยที่สุดคือการค้นหาสมดุลที่เหมาะสมระหว่างความแปรปรวนและอคติ

กล่าวอีกนัยหนึ่ง เราต้องการโมเดลที่ซับซ้อนเพียงพอที่จะจับความสัมพันธ์ที่แท้จริงระหว่างตัวแปรอธิบายและตัวแปรตอบสนอง แต่ไม่ซับซ้อนเกินไปที่จะตรวจจับรูปแบบที่ไม่มีอยู่จริง

เมื่อโมเดลซับซ้อนเกินไป โมเดลจะพอดีกับข้อมูล มากเกินไป สิ่งนี้เกิดขึ้นเพราะมันยากเกินไปที่จะค้นหารูปแบบในข้อมูลการฝึกที่เกิดจากความบังเอิญ โมเดลประเภทนี้มีแนวโน้มที่จะทำงานได้ไม่ดีกับข้อมูลที่มองไม่เห็น

แต่เมื่อแบบจำลองง่ายเกินไป ก็จะประเมินข้อมูล ต่ำไป สิ่งนี้เกิดขึ้นเนื่องจากการสันนิษฐานว่าความสัมพันธ์ที่แท้จริงระหว่างตัวแปรอธิบายและตัวแปรตอบสนองนั้นง่ายกว่าที่เป็นจริง

วิธีเลือกโมเดลที่เหมาะสมที่สุดในแมชชีนเลิร์นนิงคือการค้นหาสมดุลระหว่างอคติและความแปรปรวน เพื่อลดข้อผิดพลาดในการทดสอบโมเดลกับข้อมูลที่มองไม่เห็นในอนาคต

ในทางปฏิบัติ วิธีทั่วไปที่สุดในการลด MSE ของการทดสอบคือการใช้ การตรวจสอบข้าม