การวิเคราะห์จำแนกเชิงเส้นใน r (ทีละขั้นตอน)
การวิเคราะห์จำแนกเชิงเส้น เป็นวิธีการที่คุณสามารถใช้เมื่อคุณมีชุดตัวแปรทำนายและต้องการจัด ประเภทตัวแปรตอบสนอง เป็นสองคลาสขึ้นไป
บทช่วยสอนนี้ให้ตัวอย่างทีละขั้นตอนของวิธีการวิเคราะห์จำแนกเชิงเส้นใน R
ขั้นตอนที่ 1: โหลดไลบรารีที่จำเป็น
ขั้นแรก เราจะโหลดไลบรารีที่จำเป็นสำหรับตัวอย่างนี้:
library (MASS)
library (ggplot2)
ขั้นตอนที่ 2: โหลดข้อมูล
สำหรับตัวอย่างนี้ เราจะใช้ชุดข้อมูล ม่านตา ที่สร้างไว้ใน R โค้ดต่อไปนี้จะแสดงวิธีการโหลดและแสดงชุดข้อมูลนี้:
#attach iris dataset to make it easy to work with attach(iris) #view structure of dataset str(iris) 'data.frame': 150 obs. of 5 variables: $ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ... $ Sepal.Width: num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ... $Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ... $Petal.Width: num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ... $ Species: Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 ...
เราจะเห็นว่าชุดข้อมูลประกอบด้วยตัวแปร 5 ตัว และข้อสังเกตทั้งหมด 150 รายการ
สำหรับตัวอย่างนี้ เราจะสร้างแบบจำลองการวิเคราะห์จำแนกเชิงเส้นเพื่อจำแนกดอกไม้ที่เป็นของดอกไม้ชนิดใด
เราจะใช้ตัวแปรทำนายต่อไปนี้ในแบบจำลอง:
- กลีบเลี้ยงความยาว
- กลีบเลี้ยงกว้าง
- กลีบดอกไม้.ความยาว
- กลีบดอกไม้กว้าง
และเราจะใช้พวกมันเพื่อทำนายตัวแปรการตอบสนอง ของสปีชีส์ ซึ่งรองรับคลาสที่เป็นไปได้สามคลาสต่อไปนี้:
- เซโตซ่า
- เวอร์ซิคัลเลอร์
- เวอร์จิเนีย
ขั้นตอนที่ 3: ปรับขนาดข้อมูล
ข้อสันนิษฐานสำคัญประการหนึ่งของการวิเคราะห์จำแนกเชิงเส้นคือตัวแปรทำนายแต่ละตัวมีความแปรปรวนเท่ากัน วิธีง่ายๆ เพื่อให้แน่ใจว่าเป็นไปตามสมมติฐานนี้คือ ปรับขนาดตัวแปรแต่ละตัวให้มีค่าเฉลี่ยเป็น 0 และค่าเบี่ยงเบนมาตรฐานเป็น 1
เราสามารถทำได้อย่างรวดเร็วใน R โดยใช้ฟังก์ชัน scale() :
#scale each predictor variable (ie first 4 columns)
iris[1:4] <- scale(iris[1:4])
เราสามารถใช้ ฟังก์ชัน Apply() เพื่อตรวจสอบว่าตัวแปรทำนายแต่ละตัวมีค่าเฉลี่ยเป็น 0 และ ค่าเบี่ยงเบนมาตรฐาน เป็น 1:
#find mean of each predictor variable apply(iris[1:4], 2, mean) Sepal.Length Sepal.Width Petal.Length Petal.Width -4.484318e-16 2.034094e-16 -2.895326e-17 -3.663049e-17 #find standard deviation of each predictor variable apply(iris[1:4], 2, sd) Sepal.Length Sepal.Width Petal.Length Petal.Width 1 1 1 1
ขั้นตอนที่ 4: สร้างตัวอย่างการฝึกอบรมและการทดสอบ
ต่อไป เราจะแบ่งชุดข้อมูลออกเป็นชุดการฝึกเพื่อฝึกโมเดลและชุดทดสอบเพื่อทดสอบโมเดล:
#make this example reproducible set.seed(1) #Use 70% of dataset as training set and remaining 30% as testing set sample <- sample(c( TRUE , FALSE ), nrow (iris), replace = TRUE , prob =c(0.7,0.3)) train <- iris[sample, ] test <- iris[!sample, ]
ขั้นตอนที่ 5: ปรับโมเดล LDA
ต่อไป เราจะใช้ ฟังก์ชัน lda() จากแพ็คเกจ MASS เพื่อปรับโมเดล LDA ให้เข้ากับข้อมูลของเรา:
#fit LDA model model <- lda(Species~., data=train) #view model output model Call: lda(Species ~ ., data = train) Prior probabilities of groups: setosa versicolor virginica 0.3207547 0.3207547 0.3584906 Group means: Sepal.Length Sepal.Width Petal.Length Petal.Width setosa -1.0397484 0.8131654 -1.2891006 -1.2570316 versicolor 0.1820921 -0.6038909 0.3403524 0.2208153 virginica 0.9582674 -0.1919146 1.0389776 1.1229172 Coefficients of linear discriminants: LD1 LD2 Sepal.Length 0.7922820 0.5294210 Sepal.Width 0.5710586 0.7130743 Petal.Length -4.0762061 -2.7305131 Petal.Width -2.0602181 2.6326229 Proportion of traces: LD1 LD2 0.9921 0.0079
ต่อไปนี้เป็นวิธีการตีความผลลัพธ์ของโมเดล:
ความน่าจะเป็นก่อนหน้าของกลุ่ม: สิ่งเหล่านี้แสดงถึงสัดส่วนของแต่ละสายพันธุ์ในชุดการฝึก ตัวอย่างเช่น 35.8% ของการสังเกตทั้งหมดในชุดการฝึกเป็นของสายพันธุ์ เวอร์จิเนีย
ค่าเฉลี่ยกลุ่ม: แสดงค่าเฉลี่ยของตัวแปรทำนายแต่ละตัวสำหรับแต่ละชนิด
ค่าสัมประสิทธิ์การแบ่งแยกเชิงเส้น: ค่าเหล่านี้แสดงการรวมกันเชิงเส้นของตัวแปรทำนายที่ใช้ในการฝึกกฎการตัดสินใจแบบจำลอง LDA ตัวอย่างเช่น:
- LD1: 0.792 * ความยาวกลีบเลี้ยง + 0.571 * ความกว้างกลีบเลี้ยง – 4.076 * ความยาวกลีบกลีบ – 2.06 * ความกว้างกลีบกลีบ
- LD2: 0.529 * ความยาวกลีบเลี้ยง + 0.713 * ความกว้างกลีบเลี้ยง – 2.731 * ความยาวกลีบดอก + 2.63 * ความกว้างกลีบกลีบ
สัดส่วนการติดตาม: แสดงเปอร์เซ็นต์ของการแยกที่ได้จากฟังก์ชันจำแนกเชิงเส้นแต่ละฟังก์ชัน
ขั้นตอนที่ 6: ใช้แบบจำลองเพื่อคาดการณ์
เมื่อเราติดตั้งโมเดลโดยใช้ข้อมูลการฝึกของเราแล้ว เราสามารถใช้มันเพื่อคาดการณ์ข้อมูลการทดสอบของเราได้:
#use LDA model to make predictions on test data predicted <- predict (model, test) names(predicted) [1] "class" "posterior" "x"
ซึ่งจะส่งคืนรายการที่มีตัวแปรสามตัว:
- คลาส: คลาสที่คาดการณ์
- หลัง: ความน่าจะเป็นหลัง ที่การสังเกตเป็นของแต่ละชั้นเรียน
- x: การจำแนกเชิงเส้น
เราสามารถมองเห็นแต่ละผลลัพธ์เหล่านี้ได้อย่างรวดเร็วสำหรับการสังเกตหกครั้งแรกในชุดข้อมูลทดสอบของเรา:
#view predicted class for first six observations in test set head(predicted$class) [1] setosa setosa setosa setosa setosa setosa Levels: setosa versicolor virginica #view posterior probabilities for first six observations in test set head(predicted$posterior) setosa versicolor virginica 4 1 2.425563e-17 1.341984e-35 6 1 1.400976e-21 4.482684e-40 7 1 3.345770e-19 1.511748e-37 15 1 6.389105e-31 7.361660e-53 17 1 1.193282e-25 2.238696e-45 18 1 6.445594e-22 4.894053e-41 #view linear discriminants for first six observations in test set head(predicted$x) LD1 LD2 4 7.150360 -0.7177382 6 7.961538 1.4839408 7 7.504033 0.2731178 15 10.170378 1.9859027 17 8.885168 2.1026494 18 8.113443 0.7563902
เราสามารถใช้โค้ดต่อไปนี้เพื่อดูว่าแบบจำลอง LDA ทำนายชนิดพันธุ์ได้อย่างถูกต้องกี่เปอร์เซ็นต์:
#find accuracy of model
mean(predicted$class==test$Species)
[1] 1
ปรากฎว่าแบบจำลองทำนายสปีชีส์ได้อย่างถูกต้อง 100% ของการสังเกตในชุดข้อมูลทดสอบของเรา
ในโลกแห่งความเป็นจริง โมเดล LDA แทบจะทำนายผลลัพธ์ของแต่ละคลาสได้อย่างถูกต้อง แต่ชุดข้อมูลม่านตานี้ถูกสร้างขึ้นในลักษณะที่อัลกอริธึมการเรียนรู้ของเครื่องมีแนวโน้มที่จะทำงานได้ดีมาก
ขั้นตอนที่ 7: เห็นภาพผลลัพธ์
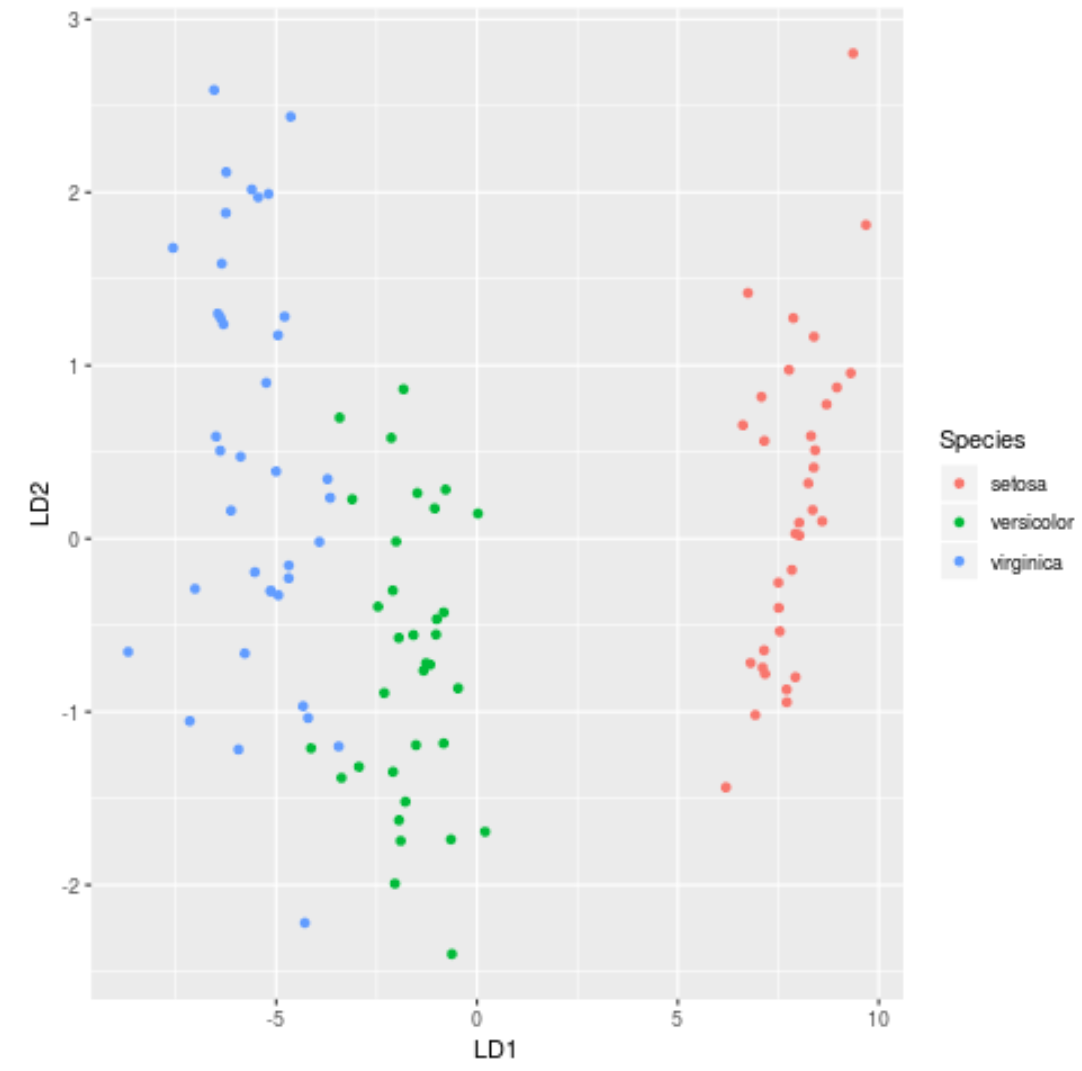
สุดท้ายนี้ เราสามารถสร้างพล็อต LDA เพื่อแสดงภาพการแบ่งแยกเชิงเส้นของแบบจำลอง และเห็นภาพว่ามันแยกสามสายพันธุ์ที่แตกต่างกันในชุดข้อมูลของเราได้ดีเพียงใด:
#define data to plot lda_plot <- cbind(train, predict(model)$x) #createplot ggplot(lda_plot, aes (LD1, LD2)) + geom_point( aes (color=Species))
คุณสามารถค้นหารหัส R แบบเต็มที่ใช้ในบทช่วยสอนนี้ ได้ที่นี่